如图示例:故:公度C2被约去以短截其长,有余则返而截,这就叫辗转相截。辗转至无余的整截式出现为止;或者是不停地辗转截下去。ri为余数,到最后一定有ri-1=miri这无余式,则ri为p、q的最大公约数,对任二整数,这样的有限辗转相除一定有。而对无公度的二线段,则只有无限辗转相截而不存在辗转除之说了。......
2023-10-21
这是中国数学家笑傲世界近两千年的光荣,也是史留辗转相截法之最靓之一例。
祖冲之,中国南北朝时期(5世纪)“专政数术”者,是数学家,也是天文学家、机械学家。《隋书·律历志》是这样述祖冲之研究圆率的:
以圆径一亿为一丈。圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,助教三丈一尺四寸一分五厘九毫二秒六忽。正数在盈朒二限间。密率:圆径一百十三,圆周三百五十五;约率:圆径七,圆周二十二。
“丈”,是中国“丈量”一事之工具,也定“单位长”。祖冲之是“以圆径D为一丈”去“丈量”圆周L,直径D怎么丈量圆周?祖冲之是“缀术”!“缀”者,针线活也!一丝线便可将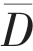 和
和 统一操作。吾复老祖宗之“缀圆”如下:实际的,祖冲之不是以D,
统一操作。吾复老祖宗之“缀圆”如下:实际的,祖冲之不是以D,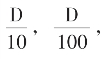 ……去度量圆,这由祖冲之的两个“率”表达便知:有“圆径”D“一百十三”,又有“圆径”D“七”,显然两率中D与L是用不同“公度”在言!所以我们可断言,祖冲之是辗转相截式地缀圆!如下图。
……去度量圆,这由祖冲之的两个“率”表达便知:有“圆径”D“一百十三”,又有“圆径”D“七”,显然两率中D与L是用不同“公度”在言!所以我们可断言,祖冲之是辗转相截式地缀圆!如下图。
L=3D+C0,D=7C0+C1,C0=15C1+C2≈16C1是祖冲之缀圆实操作得之辗转相截式,由此便有:
辗转相截式 舍入近似中止式![]() 亏值
亏值![]() 盈约去的公度
盈约去的公度
《隋书》所载祖冲之密率,约率都在其中,且都为![]() 的盈值,意在为生产、生活之实用。
的盈值,意在为生产、生活之实用。
顺便地,公元前250年,阿基米德留下的不等式 最恰当的解释,恐怕也该是L=3D+C0,D=7C0+C1两式。
最恰当的解释,恐怕也该是L=3D+C0,D=7C0+C1两式。
亏D,取D=7C0,得![]() 盈值
盈值![]() 即不等式右端;入C1时,以C1=C0,洋阿老祖宗知道误差大了,在知
即不等式右端;入C1时,以C1=C0,洋阿老祖宗知道误差大了,在知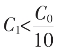 情况下,取了
情况下,取了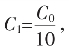 由此得
由此得![]() 亏值
亏值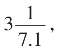 即
即![]()
洋祖宗、中国老祖宗,他们都是直击L与D之比,辗转相截法自然地用上了,这是无须任数学知识准备的方法!可惜阿基米德在“舍”“入”上没普遍性地规律化,故未能成就辗转相截法。
两“率”,我们清楚了。前两句丈、尺、寸、分、厘、毫、秒、忽长度式表述怎么读?将“比率”形式化为可直观比大小的小数,祖冲之是“以一亿为一丈”定算盘中位。
从“个”~“亿”,是计算者在算盘上之数位标,筹算、珠算,涉多位了,都要盘。故“算盘”“盘算”都是中国人计算之常用词,如同现曰“计算机”“机算”,都为依工具之成词。“以一亿为一丈”,技术性地限制了做除法,无论多高精度分式,最多七位有效小数!
依实操作截之结果
都不是《隋书》中记的七位小数言之结果。故,祖冲之应当是继续不实操作的继续辗转相截了的。由C2≈C1直观有C1=C2+C3式;再下一步我们用了“待定K”法,即设C2=KC3。
设C2=KC3,则C1=C2+C3=(K+1)C3,C0=15C1+C2=(16K+15)C3,D=7C0+C1=(113K+106)C3,L=(355K+333)C3,
此式中,![]() 是已知的盈值,
是已知的盈值,![]() 是已知的亏值。K=0,
是已知的亏值。K=0, K→∞,
K→∞,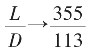 (盈值)(若视K连续,
(盈值)(若视K连续,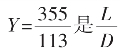 (K)的渐近线)故K自0到∞改变时,必过
(K)的渐近线)故K自0到∞改变时,必过![]() 真值点,因K取整,则必有某
真值点,因K取整,则必有某 亏而
亏而 盈。我们经由机算,得
盈。我们经由机算,得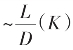 数表。从中前后逐K比较而可确定
数表。从中前后逐K比较而可确定
恰为![]() 亏盈变。我们机算的实践表明,在辗转相截的这一步,必须取十位小数才定得了相邻两K时
亏盈变。我们机算的实践表明,在辗转相截的这一步,必须取十位小数才定得了相邻两K时![]() 的亏盈恰变。
的亏盈恰变。
依分式*,历史的祖冲之可以为否?他老人家是“专政数术”的官!《隋书》文中不是有“助教”二字么?组织学生一场算盘赛是完全可以做到的,K为学生编号便可。遗憾就在“以一亿为一丈”的技术性限制,算盘上只可取七位小数,结果K=211~K=457的学生都可报出3.1415926或3.1415927的结果,确定不了C2=292C3+C4这步辗转截式和 这二精率。故只有用丈、尺、寸、分、厘、毫、秒、忽的带度量单位的长度数字表述。
这二精率。故只有用丈、尺、寸、分、厘、毫、秒、忽的带度量单位的长度数字表述。
七位小数结果只能长度式表述了!然“正值在盈朒二限间”已报告求正值还没完!
祖冲之的缀圆,本质地,已开了在弧上坐标的先河。
我们在2014年谷雨时节发出的《揭示老祖宗冲之法(辗转相截法)》一页快讯,它是中国人自己解释祖冲之圆率谜之标志!其中之表格为后来以表格式得无理数的有理逼近序列的表格法的雏形。
其实以D度量L,是先将L直化直用辗转相截法,还是将D弧化 而在圆上辗转相截,都可以。然由祖冲之之术为“缀术”,用丝线将D柔化,在圆弧上之每“截”以针线“缀”之,便为老祖宗之实。
而在圆上辗转相截,都可以。然由祖冲之之术为“缀术”,用丝线将D柔化,在圆弧上之每“截”以针线“缀”之,便为老祖宗之实。
这里我们说明了祖冲之是有可能“待定K”法的,未得K该292,293断论是受“以一亿为一丈”之技术限!这由计算机出逐K大数据表比较可得的,我儿子计算机得数表后,电话上他就先找出这可定的两优值!
“待定K”法, 一定是前面已得之一盈值,一亏值,逐K算,一定有
一定是前面已得之一盈值,一亏值,逐K算,一定有![]() 真值于某
真值于某 间,见下页表,知道存在,总有办法选出。如,在以C7为公度时,我们已得
间,见下页表,知道存在,总有办法选出。如,在以C7为公度时,我们已得![]()
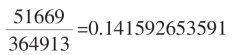 为盈值,
为盈值,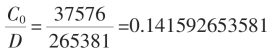 为亏值。
为亏值。
再设C7=KC8,有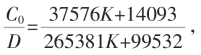 其中
其中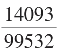 是公度C6时盈值。(www.chuimin.cn)
是公度C6时盈值。(www.chuimin.cn)
在C7=KC8这步,K=0是公度C6时盈值再现。
K=1是公度C7时盈值0.141592653591再现。
依K序,似乎是……587→……581的拖尾,而从夹![]() 真值的区间套的收缩看,不该是亏值从……581向……587之收紧么?所以这步当取K=1,K=2时值。前盈值在此踏步,而亏值取新的K=2时的
真值的区间套的收缩看,不该是亏值从……581向……587之收紧么?所以这步当取K=1,K=2时值。前盈值在此踏步,而亏值取新的K=2时的![]() 0.141592653587。
0.141592653587。
我之只用计算器之算的附表于下:
圆周率![]() 的辗转相截法计算
的辗转相截法计算
辗转相截式 舍、入近似中止辗转式![]() 亏值
亏值![]() 盈值约去的公度
盈值约去的公度
有计算机,可不必先推出 式,如续以C9为公度之计算,可
式,如续以C9为公度之计算,可
C9=1
C8=KC9
C7=C8+C9
……
C0=15C1+C2
D=7C0+C1
L=3D+C0
可作为机算语句。
打印出K,D(K),L(K),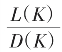 及其小数表达,再人判,定出
及其小数表达,再人判,定出![]() 恰亏盈(盈亏)变之K*,K*+1。而定C8=K*C9+C10,再继续。
恰亏盈(盈亏)变之K*,K*+1。而定C8=K*C9+C10,再继续。
在明白了L、D间的辗转相截构成的基础上,我们也可以二次方程根的形式的序列来步步近似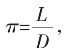 由L=3D+C0
由L=3D+C0
虽在§2中,当C0、E间是无限辗转相截时,我们称![]() 是无理数,也称
是无理数,也称 是无理数。然我们从§2到§5,都是在只论及
是无理数。然我们从§2到§5,都是在只论及![]() 故对
故对![]() 当先析出整数3。
当先析出整数3。
D=7C0+C1,D长1,C0长X,C1=1-7X。
C0=15C1+C2,C2=X-15(1-7X)=160X-15
C1=C2+C3,C3=(1-7X)-(106X-15)=-113X+16
C2=292C3+C4,C4=(106X-15)-292(-113X+16)=33102X-4687
循环节L=1,2,3,4的循环截近似:
有关辗转相截法的文章

如图示例:故:公度C2被约去以短截其长,有余则返而截,这就叫辗转相截。辗转至无余的整截式出现为止;或者是不停地辗转截下去。ri为余数,到最后一定有ri-1=miri这无余式,则ri为p、q的最大公约数,对任二整数,这样的有限辗转相除一定有。而对无公度的二线段,则只有无限辗转相截而不存在辗转除之说了。......
2023-10-21

§3、§4相应K的等比截或循环截的的根式表达式及序列递推公式一起,显然可为相应根式的数字计算式。但未盖所有正整数的开平方。的收敛条件都保证,故以换X0,上结论便转为:并注意在递推公式中,对K也无非整不可要求。不可转为步进开平方公式么?看递推式,形式的表达,代入便是在递推中,是否有形式的逼近的子序列呢,答案是肯定的。递推,便得逼近的形如的子序列。容易计算得为适合于手算开平方的三个公式。......
2023-10-21

故OX2=-E-C0,而坐标如果我们以n一般地表整数,一般地可表实数为:C0都为自nE点起,再正向(向右有)C0。有理数、无理数,我们统称为实数,数轴也称实数轴。称为逼近的单减盈有理数序列。实轴是连续直线,故实数也是连续的;直线上点有前后故实数也有前后或曰大小。在任两实数X1<X2间,都可随心所欲地嵌入无数个有理数,无数无理数!所以,实数的引入,是从可数(shǔ)个数到连续数的本质性的突变。......
2023-10-21

辗转相截结构,定为根的x的层层区间套,对每一根而言,也必有在其左右侧,f-a的反号,而mi则由恰反号的K*,K*+1定。对f,就辗转相截法而言,无须f自身性质的苛求,只要对每xk可计算,一式可,一段程序可,甚一实验也可。一般依其对f的简单认识和问题所需来。在过程中逐步加深对f的认识,更有利于求解。......
2023-10-21

下面我们先将循环节长是2的循环截推到一般。则此等式应一代数方程即pX2+pqX-q=0得这就为(p,q)循环截的的根式表达。的周期性循环节逼近原辗转截显然还可继续。不同长周期循环截尾巴。用§5中(p,q)循环截得公式方法四:视C1=7C2+C3,C2=5C3+C4,C3=6C4+C5;……则用§5中式:方法五:将所有已知五式视为无限循环截的一个循环节,则有记E长为1,C0长为X,C1长则为。的循环截逐替而逼近。这是讨论一般循环截之结论。......
2023-10-21

E=C0+C1,C0=KC1+C2,C1=C2+C3,C2=KC3+C4,……只要我们给出(m0,m1,m2,……这节,我们也试图找出(1,K)循环截的逼近的亏、盈有理序列的递推生成规律。从一个循环节得p1,q1,r1,S1,从两个循环节得p2,q2,r2,S2。),可称这为(K,1)循环截。可知,从C0=C1+C2起的无穷截为(1,K)循环截,故这便为(K,1)循环截的的根式表达。)决定的m0增大,趋向0+(1,m1……推(1,K)循环截递推公式时,为啥我们只应公度C1,C3,C5,……......
2023-10-21

先看“K等比截”一类。我们称为“K等比截”。由于每Ci-1=KCi+Ci+1起以后的无限步,与E=KC0+C1起以后的无限步是一样的,故一定有也是因此我们称之为等比截。经这样比较,我们便有递推公式从起,依此递推,得一盈、亏、盈、亏……各区间内各一个的无限个状况全知的一类无理数,K等比截一类。数值序列,可依递推公式得其欲得之精确度之近似值。K值低,收敛慢。,即C0与E有K=2X0的等比截。代则②①便表达了“K等比截”及其的根式表达式式。......
2023-10-21

“待定K”法,是确定确定而未知的的辗转相截构造的有效方法。“待定K”法,步步有衔接,每步中,必为前面已有的一盈一亏值,K=0,K→∞,为渐近线,这二值都不会再取。例如,我们解这样一方程X5=15.49638921其右端有意取1.735,我们将说明,既使用“待定K”法解方程,且由15<15.49638921<25定则这一定是在有限步“待定K”法得到。,y′=0,即tanx+x=0,代有tanx+x=0.0011459,故“待定K”法得之极大点可信(注意,若解y′=0,此方程还难解?!......
2023-10-21
相关推荐