【摘要】:下面我们先将循环节长是2的循环截推到一般。则此等式应一代数方程即pX2+pqX-q=0得这就为(p,q)循环截的的根式表达。的周期性循环节逼近原辗转截显然还可继续。不同长周期循环截尾巴。用§5中(p,q)循环截得公式方法四:视C1=7C2+C3,C2=5C3+C4,C3=6C4+C5;……则用§5中式:方法五:将所有已知五式视为无限循环截的一个循环节,则有记E长为1,C0长为X,C1长则为。的循环截逐替而逼近。这是讨论一般循环截之结论。
(1,K)循环截是在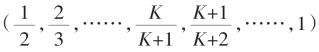 的各子区间依K不同,各嵌入一个
的各子区间依K不同,各嵌入一个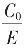 根式表达已知,逼近
根式表达已知,逼近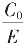 的有理序列可递推生成的无理数。
的有理序列可递推生成的无理数。
下面我们先将循环节长是2的循环截推到一般。
1.(p,q)循环截
E=pC0+C1,C0=qC1+C2,C1=pC2+C3,C2=qC3+C4,……极限地看,即都看往后的无限个辗转式,有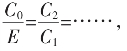 记E长为1,C0长为X
记E长为1,C0长为X
则C1长为(1-pX),C2长为X-q(1-pX)=(1+pq)X-q。
则此等式应一代数方程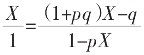
即pX2+pqX-q=0
得
这就为(p,q)循环截的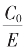 的根式表达。
的根式表达。
当p=1,q=K,就是(1,K)循环截的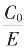 的根式表达。由(p,q)循环截我们就可在
的根式表达。由(p,q)循环截我们就可在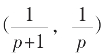 中依q不同嵌入无数个
中依q不同嵌入无数个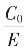 根式表达已知的无理数。
根式表达已知的无理数。
例: (3,5)循环截
代公式(1),
依§2中列表计算:
辗转相截式 舍入近似中止辗转式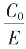 亏
亏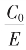 盈约去的公度
盈约去的公度
显然由这节公式(1)得的是准确值(根式表达)。如果不从它法开平方根,则由此表得有理数序列而得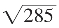 的近似值也不难。
的近似值也不难。
2.(p,q,r)循环截
E=pC0+C1,C0=qC1+C2,C1=rC2+C3,C2=pC3+C4,……极限地,有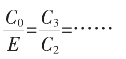
记E长为1,C0长为X,则C1=(1-pX)
C2长为X-q(1-pX)=(1+pq)X-q
C3长为(1-pX)-[r(1+pq)X-q]=-(p+r+rpq)X+1+rq,则等式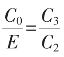 应代数方程
应代数方程
即(1+pq)X2+(p-q+r+rpq)X-(1+rq)=0
则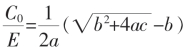
这就为(p,q,r)循环截的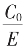 的根式表达。
的根式表达。
特别的,当p=q=1,r=K,即(1,1,K)循环截。
(1,1,K)得 当K→∞,有
当K→∞,有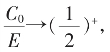 读者自己去验之。
读者自己去验之。
例:(1,1,3)循环截
由上述公式得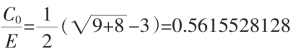
用§2中表格式,用前两周期辗转式得
(p,q,r)循环截,为在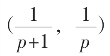 中依q变依r变,密密地可嵌入根式表达已知的无限个多无理数。
中依q变依r变,密密地可嵌入根式表达已知的无限个多无理数。
3.凡循环截,则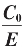 皆有二次方程根式的平方根式表达式
皆有二次方程根式的平方根式表达式
(m0,m1,……,ml-1;m0,m1,……,ml-1;……)为循环节为L长的循环截。
由E=m0C0+C1,……,CL-2=mL-1+CL-2,CL-1=m0CL+CL+1,……极限地,必有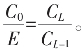
显然,各Ci的长度都可表为X的一次式,故 一定对应一二次方程,由此可得结论:
一定对应一二次方程,由此可得结论:
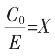 一定是此二次方程的根。
一定是此二次方程的根。
4.凡无限辗转相截过程,可由长度L=1,2,3,4,……的循环节的循环截逼近
设(m0,m1,m2,m3,……)为一无限辗转相截,
(m0,m0,m0,……)周期长为L=1的循环截
(m0,m1;m0,m1;……)周期长为L=2的循环截
(m0,m1,m2;m0,m1,m2;……)周期长为L=3的循环截
……
(m0,m1,…,mL-1;m0,m1…mL-1;……)周期长为L=L的循环截
……
L→∞“循环截”实“复原”(m0,m1,m2,……)。(数学上的∞就有如此之妙!)
由此便可肯定,任意一个无理数,总可由都是二次方程的根的平方根式表达的序列逼近!
例,(m0,m1,……)=(1,2,3,4,5,……)
求其逼近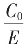 的根式序列。
的根式序列。
①记E长为1,C0长为X,求各Ci的长。
②用L=1,2,3,4……的周期性循环节逼近原辗转截
显然还可继续。当L=1,循环截(1,1,1,1,1……)与K=1等比截同;L=2,循环截为(1,2,1,2……)与K=2的(1,K)循环截同,注意§2中有理序列是“中止”辗转,只变Ci-1=miCi+Ci+1为Ci-1=miCi=miCi和Ci-1=(mi+1)Ci而有限步地返算回去。而这里是用了对以后的无限项的假设,将原无限辗转截的无限长尾巴变成了依L=1,2,3,……不同长周期循环截尾巴。所得根式值一定是在由有限一步,有限两步,……定的亏值、盈值之间。
例: (m0,m1,m2,……)=(9,1,8,7,2,1,1,5,9……)
①E长1,C0长X,求各Ci长。
②以L=1,2,3,4,5,6,7……为循环节的循环截逼近。
到现在,一个无理数的逼近,我们既有有规律操作的有理序列,又有有规律操作的平方根表达的无理数序列,丰富了§2的一般讨论。
这里举一综合应用诸方法的例子:
例 已知E=3C0+C1,C0=2C1+C2,C1=7C2+C3,C2=5C3+C4,C3=6C4+C5为一无限辗转相截的前五式,求无理数 的近似值。
的近似值。
方法一:(§2中法)
方法二:视C3=6C4+C5,……为K=6等比截,用§3公式
方法三:视C2=5C3+C4,C3=6C4+C5,……为(p,q)=(5,6)的循环截。用§5中(p,q)循环截得公式(1)
方法四:视C1=7C2+C3,C2=5C3+C4,C3=6C4+C5;……为(p、q、r)=(7、5、6)的循环截。则用§5中(2)式:
方法五:将所有已知五式视为无限循环截的一个循环节,则有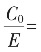

记E长为1,C0长为X,C1长则为(1-3X)。
C2长则为X-2(1-3X)=7X-2
C3长则为(1-3X)-7(7X-2)=-52X+15
C4长则为(-52X+15)-6(267X-77)=-1654X+477。
应 有
有
为-X的二次方程267X2+1577X-477=0
由此
通过这一例,将我们讲过的方法都验了一遍。方法一是§2的,方法二至方法五则是对未知的无限步作不同假设用已得公式。显然,其值都在方法一决定的亏盈二值之间。每法都是用尽已知信息,精度也都在同一水平。说明虽然我们是从不同角度讨论这无限辗转相截,但没有出矛盾!
任意一个无限辗转相截,可以用循环节L=1,2,3……的循环截逐替而逼近。而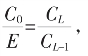 L=1,2,3……之每个假设又应一关于X(记E长为1,C0长为X)的二次方程。由此,这任意无限辗转相截生成之无理数
L=1,2,3……之每个假设又应一关于X(记E长为1,C0长为X)的二次方程。由此,这任意无限辗转相截生成之无理数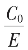 又表为了这序列二次方程根之极限!这是讨论一般循环截之结论。(www.chuimin.cn)
又表为了这序列二次方程根之极限!这是讨论一般循环截之结论。(www.chuimin.cn)
从§2开始,以辗转相截说实数。然后又以研究无限辗转相截研究无理数,没有陷入“无限不循环小数”那一把10-nE定的小巷,而是“近距离”具体畅览了这无理数世界。§2~§5只是七旬老人之跛脚导游。这样的讨论实数,会美不胜收!等着年轻的朋友!
§6的步进开平方公式序列,是在讨论等比截中之一顺手牵之一肥羊,其味也无穷。
附1:逼近无理数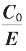 的序列的代数方程法
的序列的代数方程法
在本节处理循环截时,我们设E长为1,C0长为X,并将C1,C2……都用X的一次式表其长。这里,我们索性用等号,将E,C0,C1,……代数化。如下例:
在§2中,我们说“舍”Ci,到这里不就是让Ci=0,那里是返算回去,这里就直接解方程:
令C1=0,得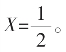 由于C1>0,即1-2X真>0,故
由于C1>0,即1-2X真>0,故 这里得的
这里得的 当为
当为 的盈值。
的盈值。
令C2=0,得 由于C2=11X真-5>0,故
由于C2=11X真-5>0,故 故这里得的
故这里得的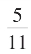 当为
当为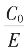 的亏值。
的亏值。
皆如此运算,我们先得由“舍”而得之各项如右:
所空之亏或盈,显然该是§2中之“入”Ci为一个Ci-1,而得。于这里,便是令Ci=Ci-1。
由C1=C0,1-2X=X,得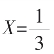
由C2=C1,11X-5=1-2X,得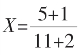
由C3=C2,41-90X=11X-5,得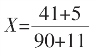
显然,空处之X值为近两亏盈值之分子加分子,分母加分母便得。
如此例,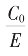 亏,
亏,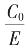 盈,序列便如右完成。
盈,序列便如右完成。
显然,只要将辗转相截式转为代数式无误,这样形成逼近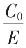 的有理亏序列,有理盈序列比§2中之返算快捷些。
的有理亏序列,有理盈序列比§2中之返算快捷些。
例:
以上则实现§2的运算。令C1=0和C1=C0,显然约去的公度也就是C0,……,步步如此!
不妨以此例再做L=1,2,3,……的循环截逼近。
前面的有理数序列,每项是从辗转截的前有限辗转步得,有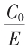 盈,
盈,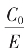 亏。而循环截逼近,是假设了以后的无限辗转是循环,假设后得的
亏。而循环截逼近,是假设了以后的无限辗转是循环,假设后得的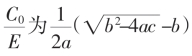 式序列的表达,故其值一定在前面的序列中相应的
式序列的表达,故其值一定在前面的序列中相应的 亏,
亏,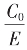 盈之间。
盈之间。
附2:对循环节全知的无限循环截都可有 的有理逼近序列的递推式和
的有理逼近序列的递推式和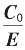 的确凿根式表达式,论述如下。
的确凿根式表达式,论述如下。
1.先看(1,K)循环截,(1,1,K)循环截、(1,1,1,K)循环截这一类
我们就以(1,1,1,K)循环截细述:
①从第一循环节得p1,q1,
这是由C2=KC3+C4对余C4作舍和入C4为一个C3,以C3为公度,返算回C0、E,然后又在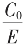 比时约去公度C3,§4节中,我们引入了“赋值句”(计算机语句),若在上面两列前面加上C3=1赋值句,则返算过程中便不见C3字母符号了,等着数值计算。
比时约去公度C3,§4节中,我们引入了“赋值句”(计算机语句),若在上面两列前面加上C3=1赋值句,则返算过程中便不见C3字母符号了,等着数值计算。
求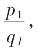 这不等式将
这不等式将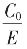 亏,
亏, 盈也表明白了。
盈也表明白了。
②从pi-1,qi-1递推pi,qi
要得pi,qi,需经过共i个循环节,要从第i个循环节开始返算,第i个循环节的最末一句是C4i-2=KC4i-1+C4i,舍C4i;或入C4i后,以C4i-1为公度返算,返算至C0得pi,返算到E是qi,而pi-1、qi-1的返算比pi、qi要少一个循环节,故只要返算式的最前加面加了赋值句C4i-1=1,则过程中全不受C4i-1字母符分干扰!!
由此便得递推式:
由于这里循环节长L=4,故递推式无盈、亏摆动而左右交叉
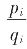 约去的是公度C4i-1不左右摆动地依i=2,3,4……递推
约去的是公度C4i-1不左右摆动地依i=2,3,4……递推
在递推式中令K=4,为(1,1,1,4)循环截,并令
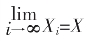 则递推式两端取极限,可得
则递推式两端取极限,可得
2014年,我们欲几何作图证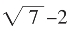 从(1,1,1,4)循环截,未果!解方程X2=7不能说其无限循环,今在此得确凿证明,并可从递推式得其欲得精度之近似值
从(1,1,1,4)循环截,未果!解方程X2=7不能说其无限循环,今在此得确凿证明,并可从递推式得其欲得精度之近似值
依 0.642857142 0.647058823
递推 0.64573991 0.645756457
仔细查读(2)式(3)式,(1,1,K)循环截,(1,K)循环截所需数据都在里边:
对(1,1,K),可查得
由于L=3,递推时盈亏摆动,有左、右交叉。
令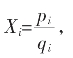 设
设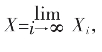 也即
也即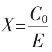 上面递推式要端取极限,便有
上面递推式要端取极限,便有
代K=9,即(1,1,9)循环截:
依
递推
显然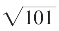 的近似值也可由此得。
的近似值也可由此得。
对(1,K)循环截,从(2)式中我们找到
从(3)中,我们找出了
由于循环节L长为2,故递推时不盈亏左右交叉摆动。
在§4中,我们是盈亏分别用字母,并左右兼看变化,才有游龙式递推,个性强并用了归纳法,也有趣味。
例:取K=3,则用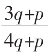 递推
递推
注意的是,这里用“赋值句”前置而避开返算过程中公度字母的纠缠,正是在§4节萌生的,所以对§4要深入领会,再是引入了“赋值句”,辗转相截句也可计算机接受了,这是年轻人的必由之路!!
这样的对已知循环节的无循环截,显然还可使因循环节短而收敛慢的循环截加速收敛。
2.长鞭打慢牛——加速算法
收敛最慢者,要算K=1的等比截,我们以十个1构成一个循环截节L=10的长循环节做无限循环截
①由第一循环节得p1,q1
②由pi-1,qi-1递推pi,qi
得pi、qi要经过10i个循环节,第10i个循环节的最后句该是C10i-2=C10i-1+C10i,舍C10i或入C10i为一个C10i-1的起返算的,要赋值句是C10i-1=1,运行到C0便为pi,到E便为qi,而pi-1,qi-1,只比pi,qi少经一个循环节,即运行到C10=C11+C12便得pi-1值,运行到C9=C10+C11便得qi-1值。
得递推公式为
由于L=10故不盈亏左右交叉摆动
依 0.617977…… 0.6180555
递推 0.618033985 0.61803399
由此可得结论:凡是已知循环节的无限循环截,都可以这样的有逼近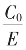 的有理数序列的递推生成,都可有用二次根式表达的确凿
的有理数序列的递推生成,都可有用二次根式表达的确凿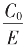 表达式,对循环节越长者,收敛得越快,对循环节L短者,可以nL为新的长循环“加鞭”!
表达式,对循环节越长者,收敛得越快,对循环节L短者,可以nL为新的长循环“加鞭”!
对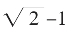 的“加鞭”!
的“加鞭”!
以九个2构成(2,2,2,2,2,2,2,2,2)循环截,依上面同样方法,可得:
递推式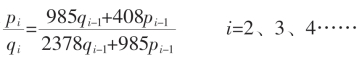
由于L=9,故递推中是盈亏摆动左右交叉。
依
对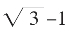 的“加鞭”!
的“加鞭”!
以五个(1,2)构成L=10的无限循环截(1,2,1,2,1,2,1,2)循环截:
由于L=10,故不盈亏摆动左右交叉。
§4将计算机用赋值句引,并将辗转相截句也用计算机算法语一样运行,这对年轻人再“辗转”,尤为必要,本册中所有方法都是计算机可为或人机对话而为的,故在§5后附此文很有必要,我是只讲过数值分析(李庆杨本)而不动手操机的,所以在众人“换笔”的时候我“拙”了!望读我册时,将数值题都能计算机上过一遍,尽量少误传!

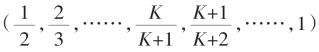 的各子区间依K不同,各嵌入一个
的各子区间依K不同,各嵌入一个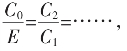 记E长为1,C
记E长为1,C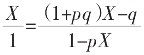
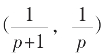 中依q不同嵌入无数个
中依q不同嵌入无数个
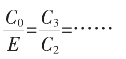
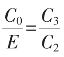 应代数方程
应代数方程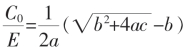
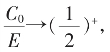 读者自己去验之。
读者自己去验之。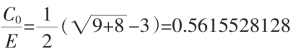
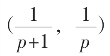 中依q变依r变,密密地可嵌入根式表达已知的无限个多无理数。
中依q变依r变,密密地可嵌入根式表达已知的无限个多无理数。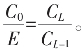
 一定对应一二次方程,由此可得结论:
一定对应一二次方程,由此可得结论: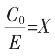 一定是此二次方程的根。
一定是此二次方程的根。 有
有
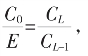 L=1,2,3……之每个假设又应一关于X(记E长为1,C
L=1,2,3……之每个假设又应一关于X(记E长为1,C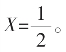 由于C
由于C 这里得的
这里得的 由于C
由于C 故这里得的
故这里得的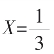
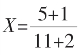
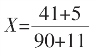
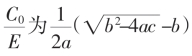 式序列的表达,故其值一定在前面的序列中相应的
式序列的表达,故其值一定在前面的序列中相应的

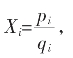 设
设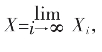 也即
也即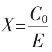 上面递推式要端取极限,便有
上面递推式要端取极限,便有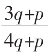 递推
递推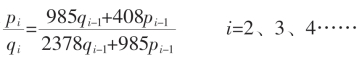





相关推荐