【摘要】:先看“K等比截”一类。我们称为“K等比截”。由于每Ci-1=KCi+Ci+1起以后的无限步,与E=KC0+C1起以后的无限步是一样的,故一定有也是因此我们称之为等比截。经这样比较,我们便有递推公式从起,依此递推,得一盈、亏、盈、亏……各区间内各一个的无限个状况全知的一类无理数,K等比截一类。数值序列,可依递推公式得其欲得之精确度之近似值。K值低,收敛慢。,即C0与E有K=2X0的等比截。代则②①便表达了“K等比截”及其的根式表达式式。
从无限辗转相截定义无理数,给我们开了研究无理数之大门。先看“K等比截”一类。
我们称为“K等比截”。由于每Ci-1=KCi+Ci+1起以后的无限步,与E=KC0+C1起以后的无限步是一样的,故一定有
也是因此我们称之为等比截。由(2)中每一等式
及相应的Ci-1=KCi+Ci+1知,图示各量关系,
于此,若记Ci-1长度为1,Ci长度为X,Ci+1长为1-KX,则有相应代数方程
由此可解得 这就为(2)中各比
这就为(2)中各比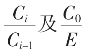 的根式表达(2)式表为
的根式表达(2)式表为
下面我们再从“舍”“入”中止辗转来讲逼近 的有理序列。
的有理序列。
在E=KC0+C1步便“舍”“入”近似为E=KC0,E=(K+1)C0而中止。
由此得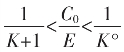 我们记此为序列的X0,约去的是C0。自
我们记此为序列的X0,约去的是C0。自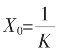 起的Xn-1的计算和Xn的计算分别两列如下:
起的Xn-1的计算和Xn的计算分别两列如下:
左边,是最后约掉Cn-1,右边是最后约掉Cn。而每一左、右相平的行的左边或右边式,K参与的运算都是一样的。除去所带的,最后要约去的公度不看,至①步,得Xn-1分子;于②步,得的是Xn-1的分母,Xn的分子;而于③之Xn的分母,是②步值(即Xn-1分母值)乘以K再加①步值(Xn-1的分子之值)。经这样比较,我们便有递推公式
从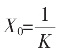 起,依此递推,得一盈、亏、盈、亏……摆动序列;再从
起,依此递推,得一盈、亏、盈、亏……摆动序列;再从 起,也依(6)递推,便得另一亏、盈、亏、盈摆动序列。依K=1,2,3,4,……之不同便得被套于
起,也依(6)递推,便得另一亏、盈、亏、盈摆动序列。依K=1,2,3,4,……之不同便得被套于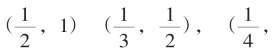
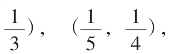 ……各区间内各一个的无限个状况全知的一类无理数,K等比截一类(见第20页表)。
……各区间内各一个的无限个状况全知的一类无理数,K等比截一类(见第20页表)。
例:由E=3C0+C1,C0=3C1+C2,……,即K=3的等比截,求其
解(www.chuimin.cn)
确凿表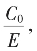 只能是根式。数值序列,可依递推公式得其欲得之精确度之近似值。
只能是根式。数值序列,可依递推公式得其欲得之精确度之近似值。
K=1,从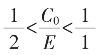 起可得
起可得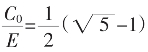 的任欲得近似值。K值低,收敛慢。从
的任欲得近似值。K值低,收敛慢。从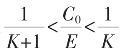 及递推时分母之乘K知,K越大,收敛(即向
及递推时分母之乘K知,K越大,收敛(即向 真值集中)越快,套
真值集中)越快,套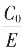 的区间套也可表为
的区间套也可表为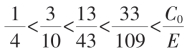
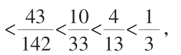 不等式串这种形式,可直观表示其区间套之逐步致紧!
不等式串这种形式,可直观表示其区间套之逐步致紧!
附:以上我们是以最简洁的文字表述。实际上(4)(5)之得到,还有另法。
方法一:从递推公式得根式表达
设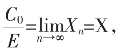 则上式两端取极限便有
则上式两端取极限便有
方法二:几何辗转截,如图
E和X0E为直角三角形二直角边,X0E为任长,即X0为任正数。
依勾股定理,有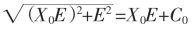
而C0与E有:E=2X0C0+C1,C0=2X0C1+C2,……,即C0与E有K=2X0的等比截。 ②
从图知,①②关系同时存在,且E>C0>C1>C2>……收敛条件不依X0如何取正实数而变。代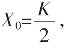 则②①便表达了“K等比截”及其
则②①便表达了“K等比截”及其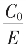 的根式表达式(5)式。
的根式表达式(5)式。
这几何图中之X0或K=2X0的不必整数要求为下面我们得步进开平方公式作了准备。

 这就为(2)中各比
这就为(2)中各比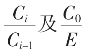 的根式表达(2)式表为
的根式表达(2)式表为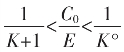 我们记此为序列的X
我们记此为序列的X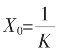 起的X
起的X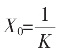 起,依此递推,得一盈、亏、盈、亏……摆动序列;再从
起,依此递推,得一盈、亏、盈、亏……摆动序列;再从 起,也依(6)递推,便得另一亏、盈、亏、盈摆动序列。依K=1,2,3,4,……之不同便得被套于
起,也依(6)递推,便得另一亏、盈、亏、盈摆动序列。依K=1,2,3,4,……之不同便得被套于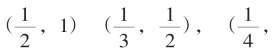
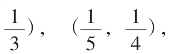 ……各区间内各一个的无限个状况全知的一类无理数,K等比截一类(见第20页表)。
……各区间内各一个的无限个状况全知的一类无理数,K等比截一类(见第20页表)。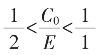 起可得
起可得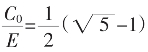 的任欲得近似值。K值低,收敛慢。从
的任欲得近似值。K值低,收敛慢。从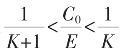 及递推时分母之乘K知,K越大,收敛(即向
及递推时分母之乘K知,K越大,收敛(即向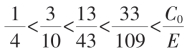
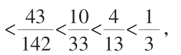 不等式串这种形式,可直观表示其区间套之逐步致紧!
不等式串这种形式,可直观表示其区间套之逐步致紧!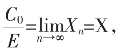 则上式两端取极限便有
则上式两端取极限便有






相关推荐