辗转相截法：实数的本质性突变

2023-10-21 理论教育版权反馈

【摘要】：故OX2=-E-C0，而坐标如果我们以n一般地表整数，一般地可表实数为：C0都为自nE点起，再正向（向右有）C0。有理数、无理数，我们统称为实数，数轴也称实数轴。称为逼近的单减盈有理数序列。实轴是连续直线，故实数也是连续的；直线上点有前后故实数也有前后或曰大小。在任两实数X1＜X2间，都可随心所欲地嵌入无数个有理数，无数无理数！所以，实数的引入，是从可数（shǔ）个数到连续数的本质性的突变。

人们从自然地数（shǔ）拇指计数起，认识了自然数（shù），罗马字或中国古人之摆筹，留下了这痕迹：

I、Ⅱ、Ⅲ、Ⅳ、V、Ⅵ、Ⅶ、Ⅷ、Ⅸ、X

1、2、3、4、5、6、7、8、9、10

一竖1为一指，一个V为一掌，一个X为两手交。再左减右加，单位数由此摆而为，多位则在一盘内分位而十进位地算，大家熟之算盘，以珠代筹棍而已。从自然数，再加减乘除，我们都是离散地数（shǔ）过来，其中“除”不就是分组数（shǔ）堆堆而已！“分”也是数（shǔ）。有限步四则运算我们所得的数（shù）便称为有理数，也是我们（人或机器）能够准确以数字写得出来的数。有理数的一般表达形式就只整数、分数（分母不能为0）和零，有理数是离散的，是可数（shǔ）的，就以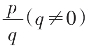 pagenumber_ebook=23,pagenumber_book=7 可一般表有理数。将分数化为小数只为放在一尺度上好直观比大小！

而当我们做衣服要量布长，要丈量土地等涉长度问题时，我们是要对每直（曲）线段说长度数了！

1.数轴和坐标

从现在起，我们是要在笔尖不离纸而画的直线上来说数了。一直线，在其上定一原点0，（origin），定一单位长线段E，此直线我们便可称为数轴，对数轴直线上每一点给其一个数，称为对这点坐标。

从原点起，以单位长E，以向右为正向，我们便逐截出1，2，3，……，正整数点；向左为负向，我们又逐截出-1，-2，-3，……，负整数点。注意的是都是在以单位长E整截。故读“3”这个点，则为自0正向截得的3E点，“-3”这个点，则为-3E点。而所言正、负整数是自原点到该点的有向线段长度。到此，原点也可读为零点。

关键是二整数点间的任X点，如图X1点，实为自原点向右截了2E后再截C0。故有向线段OX1=2E+C0，其有向长度为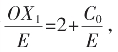 pagenumber_ebook=24,pagenumber_book=8 故表X1点的坐标为又如负向的X2点是自原点负向-E后又-C0。故OX2=-E-C0，而坐标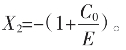如果我们以n一般地表整数，一般地可表实数为：

C0都为自nE点起，再正向（向右有）C0。

将数这样表，余下的便是依C0与E的辗转相截而展开讨论了。

当C0与E的辗转相截是有限的：E=m0C0+C1，C0=m1C1+C2，……，到Ci-1=miCi便再无余了。则Ci为C0和E的公度。返算回有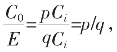 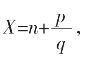pagenumber_ebook=24,pagenumber_book=8 为有理数。数轴上X点也称为有理点。

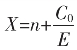当C0与E的辗转相截是无限过程：E=m0C0+C1，C0=m1C1+C2，……，Ci-1=miCi+Ci+1，……，则C0与E没有公度，表不成p/q形式，这时我们便称数轴上点为无理点，注意这为数轴上确凿的一个点，而称数 pagenumber_ebook=25,pagenumber_book=9 为无理数。

有了有理数，无理数。则数与数轴上的点实现了一一对应，对数轴上任一点，都有一坐标数，不是有理数，便是无理数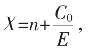， pagenumber_ebook=25,pagenumber_book=9 就依C0与E之间的辗转相截而区别。有理数、无理数，我们统称为实数，数轴也称实数轴。

2.无理数的有理序列表达

无理数C0与E的辗转相截是无限地：E=m0C0+C1，C0=m1C1+C2，……，Ci-1=miCi+Ci+1，……。然而对这无限步中的任意一步，我们都可对该步之“余”作“舍”或“入”而将该步近似表为无余式而“中止辗转”，进而得的或亏或盈的有理数近似，我们以E=C0+C1，C0=2C1+C2，C1=3C2+C3，C2=4C3+C4，……即（m0，m1，m2，m3，……）=（1，2，3，4，……）为例。列表而示之于下：

辗转相截式　舍入近似中止辗转式亏值盈值约去的公度

我们以此步中止计算为例做于下：

由C2=4C3，C1=3C2+C3=13C3，C0=2C1+C2=30C3(www.chuimin.cn)

E=C0+C1=43C3，得 pagenumber_ebook=26,pagenumber_book=10 （公度C3约掉）；

由C2=5C3，C1=3C2+C3=16C3，C0=2C1+C2=37C3

E=C0+C1=53C3，得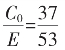 pagenumber_ebook=26,pagenumber_book=10 （公度C3约掉）。

两个值谁是亏谁是盈，最好是比较一下而定。若严格遵吾册中所用脚标，E＞C0＞C1＞C2＞……，则C1，C3……是E上余，C2，C4，……是C0上余，当亏C1，C3，……则亏E而盈，亏C2，C4，则亏。

辗转相截是无限的，这样的“中止”也是可无限的。由此我们便得无理数的有理数逼近序列。如此例：

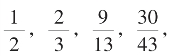pagenumber_ebook=26,pagenumber_book=10 ……称为逼近的单增亏有理数序列。

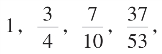pagenumber_ebook=26,pagenumber_book=10 ……称为逼近的单减盈有理数序列。

而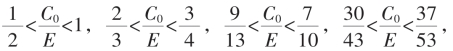 pagenumber_ebook=26,pagenumber_book=10 ……便为套住的区间套序列。

我们前面已讲，无理数是人和机都无法写尽的数。如果我们只用以上序列中某一个数，无论哪个都只能是近似数。只有序列，区间套序列可告诉我们这个写不尽之数的有理数表达的趋势。

如此例，至C8=10C9+C10。舍入近似中止式为C8=10C9和C8=11C9，再由此返算回，有

由于对任意无理数，C0与E的辗转相截是无限的，故有E＞C0＞C1＞C2＞……＞Ci-1＞Ci＞……，且随i之增大，Ci的长度从等腰直角三角形中的作图我们可直观意识得到。而从此例，至G8=10C9+C10步作“中止”，有E=7489051C9，E=8229836C9，即 pagenumber_ebook=27,pagenumber_book=11 在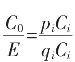的近似和无限逼近中，实际的是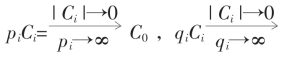E。这就是有理亏序列、有理盈序列、区间套序列的收敛的保证。

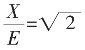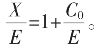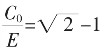再如§1中等腰直角三角形例，勾股定理是讲a2+b2=c2，这是三边关系式，几何证也是以面积证！于此，是这才是数，是仅用平方的逆运算符号表达的数轴上确凿有点而人们写不尽的数！=1.4142是其一个近似数，那么，加了……，=1.4142……，又告诉了您什么呢？而辗转相截式X=E+C0，E=2C0+C1，C2=2C1+C2，C1=2C2+C3，……，这里……告诉了您 pagenumber_ebook=27,pagenumber_book=11 的全部！请读者用本节中表格式表达，尽其情写出（提示：由X=E+C0，只求 pagenumber_ebook=28,pagenumber_book=12 便可。）

3．有理数，无理数，统称为实数，数轴也可称为实数轴

实数与实轴上点是一一对应的。实轴是连续直线，故实数也是连续的；直线上点有前后故实数也有前后（即“序”）或曰大小。

数，随数轴直线连续了。在任两实数X1＜X2间，都可随心所欲地嵌入无数个有理数，无数无理数！（x1，x2）是线段了，不管其长或短，它们上面连续的点（数）的“个数”都是一样地多。如图P与P′点的一一对应。所以，实数的引入，是从可数（shǔ）个数到连续数的本质性的突变。

连续的实数为代数中的函数的图象、为解析几何、为微积分等及其用于自然的连续运动（如运动学、力学等）的描述奠定了基础，提供了舞台。从此，我们从数（shǔ）数（shù）转入了数学分析！

表OX=nE+e1E/10+e2E/100+e3E/1000+……和OX=nE+C0都是度量式，前者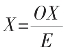 pagenumber_ebook=28,pagenumber_book=12 =n+0.e1+0.0e2+……为“小数”式表达，后者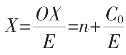仍保持度量形态。由本节的叙述可看到这种表达加上以C0与E间的辗转相截说实数，似乎方便明白得多！实数是依数轴直线而连续的，“不连续”只会发生某些“数学问题”或“数学命题”对自己“论域”或“定义域”的特殊要求而来！只从离散有理数系起依数运算之增加而公理式做的数系扩张，至今还未见将实数的连续讲得明白透彻者。如下面摘的以公理说实数和超实数者，在其中以“公理”说实数的Ⅰ、Ⅱ、Ⅲ中，如果除去Ⅱ“实数的序公理”中的F“开根公理”，就只能是从0、1起以运算构造的“有理数系”，而加进一个开根公理，就是“实数系”了吗？ pagenumber_ebook=29,pagenumber_book=13 是从0、1起经加、减、乘、除、乘方、开方而出的实数吗？

辗转相截法：实数的本质性突变

相关推荐