增生算子方程的逼近理论

2023-10-20 理论教育版权反馈

【摘要】：在增生算子的理论中,一个归功于Browder 的早期的基本成果是,若T是E 上的局部李普希兹增生算子,则初值问题有解.进一步利用该方程的存在性结果,Browder 证明了如果T 是局部李普希兹连续的增生算子,则T 是m-增生的.特别地,对任意的f∈E,方程x＋Tx=f 有解,后来Martin 证明了当T 是连续增生算子时,上面的初值问题有解,从而推广了Browder 的结果.而且利用该结果,他还证

在增生算子的理论中,一个归功于Browder 的早期的基本成果是,若T是E 上的局部李普希兹增生算子,则初值问题

有解.进一步利用该方程的存在性结果,Browder 证明了如果T 是局部李普希兹连续的增生算子,则T 是m-增生的.特别地,对任意的f∈E,方程x＋Tx=f 有解,后来Martin 证明了当T 是连续增生算子时,上面的初值问题有解,从而推广了Browder 的结果.而且利用该结果,他还证明了当T 是连续增生算子时,T 是m-增生算子.

对于方程x＋Tx=f 的解,除了对其存在性进行了研究,不少学者还对其近似解做了逼近.

定理1　设E 是一个Banach 空间,T:D(T)=E→E 是李普希兹连续的增生算子.又设{αn},{βn}是实序列,满足下列条件:

则对任给的x0∈E,下列序列

yn=(1-βn)xn＋βn(f-Txn),

xn＋1=(1-αn)xn＋αn(f-Tyn)

强收敛于方程x＋Tx=f 的唯一解,而且,若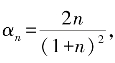 pagenumber_ebook=174,pagenumber_book=167 则

其中,x∗是方程x＋Tx=f 的唯一解.

如果算子T 是强增生的,则T-I 是增生的,可通过如下定理获得方程Tx=f 的解.

定理2　设E 是一个Banach 空间,T:D(T)=E→E 是李普希兹的强增生算子.又设{αn},{βn}是实序列,满足下列条件:(www.chuimin.cn)

则对任给的x0∈E,下列序列

yn=(1-βn)xn＋βn(f-Txn＋xn),

xn＋1=(1-αn)xn＋αn(f-Tyn＋yn)

强收敛于方程Tx=f 的唯一解.

对于m-增生算子T 的零点集,记作T-1(0)={x:0∈Tx}.为了获得增生算子的零点,人们也分别进行了存在性研究以及近似解的逼近研究.对于增生算子零点逼近的一个经典的迭代法叫作近端点算法,即x1∈E

xn＋1=Jλnxn,

其中Jλn=(I＋λnT)-1 为T 的预解式.该迭代算法在适当的条件下,弱收敛于T 的零点.但是,它无法保证强收敛.因此在增生算子的零点方程求解过生中,人们转向于对算法进行修正,以使其能够强收敛于增生算子方程Tx=0 的解.

定理3　设E 是一致凸的Banach 空间,其范数是一致Gateaux 可微的,C 是E 的非空闭凸子集,T ⊂E × E 为增生算子,序列{αn}⊂(0,1],λn>0.假设T-1(0)是非空的,对任意的λ>0,D(T)⊂C ⊂R(I＋λT),且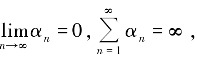 pagenumber_ebook=175,pagenumber_book=168 inf λn>0.其中是D(T)的闭包,I 是单位算子.令u 为C 中的任一点,x1为C 中的任一点,则序列

xn＋1=αnu＋(1-αn)Jλnxn,

强收敛于Qu,Q 是C 在T-1(0)上的唯一sunny 非扩张收缩.

增生算子方程的逼近理论

相关推荐