单调算子与增生算子的迭代逼近及应用

2023-10-20 理论教育版权反馈

【摘要】：)∈l∞使得μ≤α 对任意的Banach 极限.若≤0,则≤α.

对于非线性全连续算子方程,常可用拓扑度理论来研究它的解.但应用上出现的有些非线性算子不是全连续的,而是所谓单调算子(映像).这时,常可用单调映像的理论来研究这类方程的解.单调映像理论是近20 多年发展起来的,是非线性泛函分析的重要分支之一,它在非线性偏微分方程、非线性积分方程以及Banach 空间微分方程等方面都有应用.

本节将介绍单调算子以及增生算子的基本概念和相关性质.

设E 是实Banach 空间,E∗是E 的共轭空间.对于x ∈E,f ∈E∗,记〈f,x〉=f(x).

定义1　设D⊂E,映像T:D→E∗.若满足条件

〈Tx-Ty,x-y〉≥0,∀x,y∈D

则称T 是单调映像.若上式的等号仅在x=y 时成立,则称T 为严格单调映像.

注1　集合G⊂E×E∗称为单调集,如果满足:

〈y1-y2,x1-x2〉≥0,∀[x1,y1],[x2,y2]∈G

显然,对于映像T:D→E∗,它是单调映像的充要条件是它的图像G(T)=是空间E×E∗中的单调集.

注2　①若T1:D→E∗,T2:D→E∗都是单调映像,则T1＋T2:D→E∗也是单调映像;

②若T:D→E∗是单调映像,λ≥0,则λT:D→E∗是单调映像;

③对于线性算子T:D→E∗,T 单调⇔〈Tx,x〉≥0,∀x∈D.

例1　设H 是希尔伯特空间,A:H→H 是非扩张映像,即

‖Ax-Ay‖≤‖x-y‖,∀x,y∈H,

则T=I-A:H→H 必定是单调映像.事实上,有

例2　设Wm,p(Ω)是索伯列夫空间.伪Laplace 映像T: pagenumber_ebook=170,pagenumber_book=163 :

是单调映像.

单调映像的概念可以推广到多值映像(集值映像).以下用2E∗表示空间E∗的一切子集所成的集.对于多值映像T:E→2E∗,记

D(T)={x|x∈E,Tx≠∅}为T 的有效域;

R(T)={y|y∈Tx,x∈D(T)}为T 的值域;

G(T)={[x,y]|[x,y]∈E×E∗,y∈Tx,x∈D(T)}为T 的图像.

定义2　对于多值映像T:E→2E∗

①如果值域R(T)=E∗,则称T 是满射的;

②如果T 把D(T)中的任何有界集S 映成E∗中的有界集,则称T 是有界的;

③给定x0∈E.若存在x0在E 中的某邻域U(x0)使得U(x0)∩D(T)≠∅,且T(U(x0)∩D(T))={y|y∈Tx,x∈U(x0)∩D(T)}在E∗中有界,则称T 在x0处是局部有界的.

定义3　单调集M⊂E×E∗,如果不是E×E∗中的任何单调集的真子集,则称集合M 是极大单调的.多值映像T:E→2E∗称为单调的是指,它的图像G(T)是E×E∗中的单调集;T 是极大单调的是指,它的图像G(T)是E×E∗中的极大单调集.

定义4　设D⊂E,映像T:D→E∗.(www.chuimin.cn)

①设x0∈D,若xn∈D,xn→x0⇒Txn⇀Tx0,则承T 在x0处是次连续的;若T 在D 中每一点都次连续,则称T 在D 上次连续.

②设x0∈D,若h∈E,tn>0,x0＋htn∈D,tn→0⇒T(x0＋htn)⇀Tx0,则称T在x0处是半连续的;若T 在D 中每一点都半连续,则称T 在D 上半连续.

注3　显然,T 在x0处是次连续⇒T 在x0处是半连续;T 在x0处是次连续⇒T 在x0处局部有界.

定义5　设C 为Banach 空间E 的非空闭凸子集,称映射T:C→E 是α-逆强单调的,若存在正实数α,使得

〈Tx-Ty A#,x-y〉≥α‖Tx-Ty‖2,∀x,y∈H,

定义6　设T:E→2E∗是一个极大单调映像且λ>0.算子JTλ:E→D(T)定义如下:

称其为T 的预解式.

定义7　正规对偶映射J:E→2E∗为如下定义

Jx={x∗∈E∗:‖xx∗‖=‖x∗‖2=‖x‖2},

其中<·,·>表示E 和E∗z 之间的正规对偶对.众所周知,如果E 是光滑的当且仅当J 是单值的;如果E 是一致光滑的那么J 在E 的有界子集上是一致连续的.在希尔伯特空间中,J 是单位算子.

定义8　设C 是Banach 空间E 的闭凸子集,称映像T:C→E 为增生的,如果存在j(x-y)∈J(x-y)使得

〈j(x-y),Tx-Ty〉≥0.

显然,若E 为希尔伯特空间,则增生映像与单调映像是一致的.

注4　①设E 是希尔伯特空间,T:E→2E∗是值集映射.则如下几点是等价的:

a.T 是单调的;

b.T 是增生的,即,对于任意的(x,x∗)∈graT 且(y,y∗)∈graT

‖(x-y)‖＋α(x∗-y∗)‖≥‖x-y‖,∀α∈[0,1].

②若T:E→2E∗是一个极大单调映像且λ>0,则预解式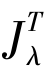 pagenumber_ebook=172,pagenumber_book=165 是单值映射且是非扩张的;

③若T:E→2E∗是一个极大单调映像且λ>0,则预解式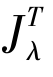 pagenumber_ebook=172,pagenumber_book=165 是严格非扩张的且是平均的.

引理1　设{an}是非负实数列且满足下列关系:

an＋1≤(1-θn)an＋σn,　n≥0,

其中{θn}和{σn}是实数列使得

则序列{an}收敛于0.

引理2　设E 是具有对偶空间E∗的实Banach 空间.令J:E→E∗是正规对偶映射,则对所有的x,y∈E,

‖x＋y‖2≤‖x‖2＋2〈y,j(x＋y)〉,∀j(x＋y)∈J(x＋y).

引理3　设α 是实数,且(x0,x1,…)∈l∞使得μ(xn)≤α 对任意的Banach 极限.若≤0,则≤α.

单调算子与增生算子的迭代逼近及应用

相关推荐