细观模型的边界条件和损伤断裂模式有比较直接的关系,本节在模型左、右两端考察了三种边界条件对计算结果的影响。在上端采用垂直位移加载控制来模拟单轴拉伸和压缩条件。在下端施加垂直方向约束。计算结果和Arora 等[16]得到的结论一致。图8-16拉伸载荷下三种边界条件的计算结果自由边界;耦合直边;周期性边界图8-17压缩载荷下三种边界条件的计算结果自由边界;耦合直边;周期性边界......
2025-09-29
设H 是一个实Hilbert 空间,其内积和范数分别表示为〈·,·〉 和‖·‖,K 是一个H 中的非空闭凸集.T∶H→H 是一个非线性映射,g∶H→H 是一个非线性连续可逆映射.
考虑包含非线性算子的一般变分不等式问题:求u ∈H,g(u)∈K 满足
〈Tu,g(v)-g(u)〉 ≥0,∀g(v)∈K.
当g=I 时,即转化为经典的变分不等式问题:
〈Tu,v-u〉 ≥0,∀v ∈K.
定义1 称映射T∶H→H 为g-μ-Lipschitzian 连续:如果存在常数μ>0,使得
‖Tx-Ty‖≤μ‖g(x)-g(y)‖,∀g(x),g(y)∈K.
定义2 称映射T∶H→H 为g-r-强单调:如果存在常数r>0,使得
〈Tx-Ty,g(x)-g(y)〉 ≥r‖g(x)-g(y)‖2,∀g(x),g(y)∈K.
定义3 称映射T∶H→H 为g-α-强制:如果存在常数α>0,使得
〈Tx-Ty,g(x)-g(y)〉 ≥α‖Tx-Ty‖2,∀g(x),g(y)∈K.
定义4 称映射T∶H→H 为g-(γ,r)-松弛强制:如果存在常数γ>0,r>0,使得
〈Tx-Ty,g(x)-g(y)〉 ≥-γ‖Tx-Ty‖2+r‖g(x)-g(y)‖2,∀g(x),g(y)∈K.
注1 当g=I 时,上述各项定义即转化为文献[15] 中定义的μ-Lipschitzian 连续、r-强单调、α-强制和(γ,r)-松弛强制.
注2 g-r-强单调映射一定是g-(γ,r)-松弛强制映射,但其逆命题并不成立.因此,g-(γ,r)-松弛强制映射是比g-r-强单调映射更一般的映射.
引理1 设{an},{bn},{λn}为三个非负数序列,如果λn∈[0,1] 且满足不等式:
an+1≤(1-λn)an+bn,∀n ≥0,
其中, ,则
,则![]() =0.
=0.
引理2 如果一个给定的u ∈H,g(u)∈K 为上面变分不等式问题的解,当且仅当
g(u)=PK[g(u)-ρTu],ρ>0,
其中PK为H 在K 上的投影,PK为非扩张映射.
定理1 设u∗是一般变分不等式问题(1)的解,T 为g-(γ,r)-松弛强制映射且g-μ-Lipschitzian 连续,则
‖PK[g(un)-ρTun]-g(u∗)‖2≤(1-2ρr+2ργμ2+ρ2μ2)‖g(un)-g(u∗)‖2.
证明 由引理2 和T 为g-(γ,r)-松弛强制映射且g-μ-Lipschitzian 连续,则
定理2 设u∗是一般变分不等式问题(1)的解,T 为g-(γ,r)-松弛强制映射且g-μ-Lipschitzian 连续.如果σn,λn,αn,βn,γn∈[0,1],并满足下列条件:
则由算法:对一个给定的u0∈H,g(u0)∈K,由下列迭代格式计算un+1:
得到的序列{un}收敛到u∗,即![]() =u∗.
=u∗.
证明 由条件(ⅰ)和定理1,得
‖PK[g(un)-ρTun]-g(u∗)‖≤θ‖g(un)-g(u∗)‖,
其中,θ=![]() ,0 < θ < 1.
,0 < θ < 1.
同理可得
‖PK[g(vn)-ρTvn]-g(u∗)‖≤θ‖g(vn)-g(u∗)‖,
‖PK[g(wn)-ρTwn]-g(u∗)‖≤θ‖g(wn)-g(u∗)‖.
由引理2 得
类似地,有
‖g(wn)-g(u∗)‖≤‖g(un)-g(u∗)‖.
由式(ⅱ)和引理2,得
由引理1 得![]() -g(u∗)‖=0.又因为g 是连续可逆映射,因此
-g(u∗)‖=0.又因为g 是连续可逆映射,因此![]() ,即
,即![]() =u∗.(https://www.chuimin.cn)
=u∗.(https://www.chuimin.cn)
定理3 设u∗是变分不等式问题(2)的解,T 为(γ,r)-松弛强制映射且μ-Lipschitzian 连续.如果σn,λn,αn,βn,γn∈[0,1],并满足下列条件:
则由算法:对一个给定的u0∈H,由下列迭代格式计算un+1:
得到的序列{un}收敛到u∗,即![]() =u∗.
=u∗.
证明 在定理2 的证明中令g=I,同理可证.
下面研究一类非凸变分不等式问题:设T 为非线性算子,Kr为Hilbert空间H 中的非凸子集,求u ∈Kr,使得
〈Tu,v-u〉 ≥0,∀v ∈Kr.
Wiener-Hopf 方程与变分不等式问题存在紧密联系,为了方便表示,设QKr=I -SPKr,其中PKr是投影算子,I 是单位算子,S 为非扩张映象.对于给定的非线性算子T,求z ∈H 满足
TSPKrz+ρ-1QKrz=0.
称该式为非线性Wiener-Hopf 方程,当r=∞,S=I 时,方程退化为求解经典变分不等式问题的辅助wiener-Hopf 方程.
设u 为Hilbert 空间H 中的一点,以![]() 表示H 到K 的距离,称
表示H 到K 的距离,称
为K 在u 的近似正规锥,其中PK[u]={u∗∈K∶dK(u)=‖u-u∗‖}.称![]() 为Clarke 正规锥,其中
为Clarke 正规锥,其中![]() 表示凸集的闭包.显然,
表示凸集的闭包.显然,![]() 且
且![]() 是闭凸集,但近似正规锥
是闭凸集,但近似正规锥![]() 是凸集,却不一定是闭集[61].
是凸集,却不一定是闭集[61].
设Kr为H 中的一个非空子集,对给定的常数r ∈(0,∞],如果Kr的每一个非零近似正规锥![]() 都可以表示为一个r-球,即对任意u ∈Kr和
都可以表示为一个r-球,即对任意u ∈Kr和![]() ,满足
,满足
则称Kr为一致近似正规集.
一致近似正规集包含凸集,p-凸集,H 中的C1,1 子流形(可能包含边界)等类型的凸集和非凸集.如果r=∞,则一致近似正规集Kr与K 等价,即Kr=K; 如果Kr是一致近似正规集,则近似正规锥![]() 是闭的集值映象,所以
是闭的集值映象,所以![]() .
.
引理3 设K 为H 的非空闭子集,如果Kr={u ∈H∶d(u,K)< r}是一致近似正规集,则
(ⅰ)∀u ∈Kr,PKr(u)≠0.
(ⅱ)∀r′∈(0,r),PKr是δ-Lipschitz 连续算子,其中常数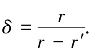
(ⅲ)近似正规锥![]() 是闭的集值映象.
是闭的集值映象.
引理4 u ∈Kr为非凸变分不等式(1)的解的充分必要条件是u=PKr[u-ρTu],其中![]() 为H 在一致近似正规集Kr上的投影.
为H 在一致近似正规集Kr上的投影.
设S∶Kr→Kr为非扩张映象,F(S)表示S 的不动点集,以VI(T,Kr)表示非凸变分不等式的解集,WHE(T,S)表示Wiener-Hopf 方程的解集,并且假设F(S)∩WHE(T,S)≠∅.
记F(u)=PKr[u-ρTu],则F(u)的不动点即非凸变分不等式的解.据此,分析非凸变分不等式问题和非线性Wiener-Hopf 方程的等价性.
定理4 u∗∈F(S)∩VI(T,Kr)的充分必要条件是z∗∈WHE(T,S),并满足
u∗=SPKrz∗,z∗=u∗-ρTu∗.
证明 设u∗∈F(S)∩VI(T,Kr),由引理2 得
u∗=Su∗=PKr[u∗-ρTu∗]=SPKr[u∗-ρTu∗].
并且该式可以另记为
u∗=SPKrz∗,z∗=u∗-ρTu∗.
所以z∗恰好是非线性Wiener-Hopf 方程的解.
z∗=u∗-ρTu∗=SPKrz∗-ρTSPKrz∗,
定理5 设Kr为H 中的一致近似正规子集,PKr是δ-Lipschitz 连续算子,其中 ,∀r′∈(0,r).设T∶Kr→Kr为松弛(γ,r)-余强制映象且μ-Lipschitz 连续.如果
,∀r′∈(0,r).设T∶Kr→Kr为松弛(γ,r)-余强制映象且μ-Lipschitz 连续.如果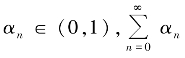 =∞,且常数ρ>0 满足
=∞,且常数ρ>0 满足
则由算法定z0∈H,
得到的序列{zn}收敛到z∗∈F(S)∩WHE(T,S).
证明 设u∗∈F(S)∩WHE(T,S),由(3)式和定理1 得
由于T 为(γ,r)-松弛强制映象且μ-Lipschitz 连续,因此
由S 的非扩张性得
其中![]() 由(6)式不难验证θ ∈(0,1),进一步整理得
由(6)式不难验证θ ∈(0,1),进一步整理得
因为 ,且θ ∈(0,1),所以
,且θ ∈(0,1),所以 0.由(10)式得
0.由(10)式得![]() ‖zn-z∗‖=0,即序列{zn}收敛到z∗∈F(S)∩WHE(T,S).
‖zn-z∗‖=0,即序列{zn}收敛到z∗∈F(S)∩WHE(T,S).
相关文章

细观模型的边界条件和损伤断裂模式有比较直接的关系,本节在模型左、右两端考察了三种边界条件对计算结果的影响。在上端采用垂直位移加载控制来模拟单轴拉伸和压缩条件。在下端施加垂直方向约束。计算结果和Arora 等[16]得到的结论一致。图8-16拉伸载荷下三种边界条件的计算结果自由边界;耦合直边;周期性边界图8-17压缩载荷下三种边界条件的计算结果自由边界;耦合直边;周期性边界......
2025-09-29

蜀国的材料不多,满想下手整理,写一篇古蜀国的传说。不幸历代人士为秦汉的大一统思想所陶冶,认为古代也是一模一样的,终不肯说这一块土地上的文化在古代独立发展,偏要设法把它和中原的历史混同搅和起来,于是处处勉强拍合,成为一大堆乱丝。彼此纠缠,把人们的脑筋弄迷糊了,古蜀国的真相,再也看不清了。现在就写出这一篇,做古蜀国史研究的一个引子。......
2025-09-29

西美尔认为时尚外在于个体,时尚向个体展现的易变性是个体自我稳定感的对照,在对照中,个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为,作为一种大众行为,时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中,西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29

国家财政的原则国家财政的原则,一般地说,应该是“量出为入”,因为社会愈进化,人类愈文明,则公共财政支出的数字也愈庞大,国家在编制预算时,如果支出增加,国库的收入可由增加税率以谋相适应的增加。我国这方面支出的绝大部分是供养将近300万军人的薪水与公费。事实上,在这巨额债务费的支出中,差不多有半数是偿付外债的本息与赔款的。第二则为非真正的岁入,即债款。第三是其他收入,如国营事业收入等。......
2025-09-29

,cn)是依赖于参数c0,c1,…,cn的初等函数.用P(x,c0,c1,…,cn)来近似表示f,要求选择一组参数使误差最小.这就是寻求极小问题的解.当参数给出最小误差时,就把叫作f在P(x,c0,c1,…,cn)所构成的函数类中的一个最佳逼近元;数值P叫作f借助于函数P(x,c0,c1,…......
2025-09-30

发明与“技术”和“工艺”相关联。发明是用客观规律改造客观,创造出原先不存在的客观,发明与发现密切相关。重大的科学发现可能会导致一系列的技术发明;技术上的重大突破也会引起科学上的重大发现。发现是通过观察事物而发现其原理;发明是根据发现的原理而进行制造或运用,产生出一种新的物质或行动。例如,古人发现水有浮力,于是根据这一原理“刳木为舟”,把大木头挖空,造成独木舟,这叫发明。......
2025-09-29

大学专业与未来职业发展的具体关系如下。大学系统的专业学习为职业发展对专业知识技能的需求提供了保障。大学生要通过自己专业知识的学习,充实自己的专业技能,开阔自己的眼界,提升自我的素质,确定自己的职业发展目标,以达到社会对职业素质的要求,成为一名合格的职业者。......
2025-09-30

浓厚蛋白与蛋的质量、贮藏、加工有着密切的关系,含有溶菌酶,它具有溶解微生物膜的特性,因此有抑制和杀灭侵入的微生物的作用。随着蛋存放时间的延长,或受外界较高气温等因素的影响,溶菌酶也逐渐减少,以至完全消失,蛋便失去了抑菌和杀菌的能力,此时侵入蛋内的微生物便生长繁殖,使蛋发生腐败变质。稀薄蛋白约占蛋白总量的 45% 左右,呈水样胶体,不含溶菌酶。淡卵黄柱向外延伸至蛋黄膜下,其喇叭形的口部托着胚珠。......
2025-09-29
相关推荐