布劳威尔不动点定理是代数拓扑的早期成就,还是更一般的不动点定理的基础,在泛函分析中尤其重要.1904年,首先由Piers Bohl 证明n=3 的情况(发表于《纯粹及应用数学期刊》 之内).1909年,鲁伊兹·布劳威尔(L.E.Brouwer)再次证明.1910年,雅克·阿达马提供一般情况的证明,而布劳威尔在1912年提出另一个不同的证明.这些早期的证明皆属于非构造性的间接证明,与数学直觉主义理想......
2023-10-20
E 为一实Banach 空间,E∗为E 的对偶空间,〈·,·〉表示广义对偶对,称J∶E→2E∗为正规对偶映像,如果
Jx={f ∗∈E∗∶〈x,f ∗〉=‖x‖2=‖f ∗‖2},∀x ∈E.
今后均用j 表示单值赋范对偶映射.若E 中存在序列{xn}弱收敛到x,使得J(xn)依范数弱收敛到J(x),则称E 具有弱连续对偶映射.
若S={x ∈E∶‖x‖=1}为E 的单位球面,对任意的x,y ∈ 一致存在,则称E 的范数是一致Gateaux 可微的.设E 为一实Banach 空间,C 为E 的一个非空闭凸子集.若映射T∶C→C满足条件
一致存在,则称E 的范数是一致Gateaux 可微的.设E 为一实Banach 空间,C 为E 的一个非空闭凸子集.若映射T∶C→C满足条件
‖Tx-Ty‖≤‖x-y‖,∀x,y ∈C,
则称T 为非扩张的映射.记F(T)为T 的不动点集,即F(T)={x ∈C∶Tx=x}.若映射f∶C→C,存在一个实数ρ ∈(0,1)并且满足
‖f(x)-f(y)‖≤ρ‖x-y‖,∀x,y ∈C,
则称f 为具有系数ρ 的压缩映射.
引理1 设C 为实Banach 空间E 的非空闭凸子集.T∶C→C 为非扩张映射,F(T)≠ϕ.对任意固定的u ∈E 以及t ∈(0,1),则由x|→tu+(1-t)Tx 所定义的压缩算子的唯一不动点zt,在t→0 时强收敛于p ∈F(T),其中p 是与u 的距离最近的一点.
引理2 设E 为一实Banach 空间,E∗为E 的对偶空间,J∶E→2E∗为正规对偶映像,则对任意的x,y ∈E,有
‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉,∀j(x+y)∈J(x+y).
引理3 设E 为具有一致Gateaux 可微范数的实Banach 空间,则正规对偶映像J 是单值的且在E 的任意有界子集上由E 的范数拓扑到E∗的弱拓扑是一致连续的.
引理4 设{an},{bn},{cn}均为非负实数列,对任意λn∈[0,1],若存在正整数N 使得
an+1≤(1-λn)an+bn+cn,∀n ≥N.
其中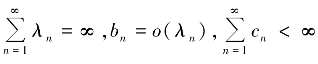 ,则
,则![]() =0.
=0.
称序列{xn}满足条件(C):设E 是一个实Banach 空间,Tn∶C→C 是一族非扩张映射,若序列{xn}弱收敛于x 且xn-Tnxn→0,则x ∈F,其中F=∩n≥1F(Tn).
假设C ⊆E 是有界闭凸子集,称映射Q∶E→C 为阳光的;若Q(tx+(1 -t)Q(x))=Q(x),称映射Q∶E→E 是压缩的映射,当且仅当Q2=Q.若Q 是压缩的,则Q(z)=z,∀z ∈R(Q),其中R(Q)是Q 的值域.
引理5 设C 是光滑Banach 空间E 的非空子集.Q∶E→C 是一个压缩映射.J 是常规对偶映射,则如下几条等价:
(ⅰ)Q 是阳光非扩张的;
(ⅱ)〈x-Q(x),J(y-Q(x))〉≤0,∀x ∈E,y ∈C.
定理1 设C 为实Banach 空间E 的非空闭凸子集,T∶C→C 为非扩张映射,f∶C→C 为具有系数ρ 的压缩映射.如果定义算子:
其中t ∈(0,1),n ≥0,则Tt,n是压缩的,且Tt,n的不动点列强收敛到T 的不动点.
证明 设∀x,y ∈C,由f 的压缩性以及T 的非扩张性,得
因为ρ ∈(0,1),所以0 < 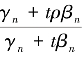 < 1,即Tt,n为压缩映射.由Banach 压缩映象原理可知,Tt,n存在唯一的不动点,记作pt,n,即
< 1,即Tt,n为压缩映射.由Banach 压缩映象原理可知,Tt,n存在唯一的不动点,记作pt,n,即
由引理1,得![]() =pn∈F(T).假设存在另一个不动点pm,且
=pn∈F(T).假设存在另一个不动点pm,且![]() =pm,则pn,pm均是距f 的不动点最近的点.因此pn=pm=p ∈F(T),所以
=pm,则pn,pm均是距f 的不动点最近的点.因此pn=pm=p ∈F(T),所以![]() p ∈F(T).
p ∈F(T).
定理2 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.T∶C→C 为非扩张映射,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理1 所定义的压缩映射.如果实数序列{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足下列条件:
则由得到的序列
{xn}有界,且强收敛于T 的不动点p,其中p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C.
证明 设p ∈F(T),由T 的非扩张性得
‖yn-p‖=‖εnxn+(1-εn)Txn-p‖≤‖xn-p‖.
对于∀n ≥0,由T 的非扩张性和f 的压缩性,有
记 ,则‖xn-p‖≤M1.所以{xn}有界,进一步可得{yn},{Txn},{Tyn}均有界.
,则‖xn-p‖≤M1.所以{xn}有界,进一步可得{yn},{Txn},{Tyn}均有界.
另一方面,由引理2 可知
若记M2=sup‖xn-p‖2,整理上式得
由定理1,不妨设pt,n为Tt,n的唯一不动点,将定理1 所得的pt,n另记为
于是
所以
其中M3=sup{‖xn-Txn‖2+2‖xn-Txn‖‖xn-pt,n‖,n ≥0}.由条件(ⅲ)得
其中M4≥sup{‖pt,n-xn‖2,0 < t < 1,n ≥0}.得
又因为![]() =p,所以
=p,所以
得
记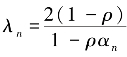 αn,则由和引理4,可知
αn,则由和引理4,可知![]() ‖xn-p‖=0,即{xn}强收敛于p ∈F(T),且p 是变分不等式〈p-f(p),x-p〉 ≥0,∀x ∈C 的解.
‖xn-p‖=0,即{xn}强收敛于p ∈F(T),且p 是变分不等式〈p-f(p),x-p〉 ≥0,∀x ∈C 的解.
若另外有一个 也是变分不等式〈p-f(p),x-p〉 ≥0,∀x ∈C 的解,则
也是变分不等式〈p-f(p),x-p〉 ≥0,∀x ∈C 的解,则
以及
将两式相加,得‖p-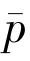 ‖2≤ρ‖p-
‖2≤ρ‖p-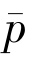 ‖2,0 < ρ < 1.所以p=
‖2,0 < ρ < 1.所以p= ,因此p 是满足如下变分不等式的唯一解:
,因此p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C
定理3 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.T∶C→C 为非扩张映射,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理2 所定义的压缩映射.如果定义序列
xn+1=αnf(xn)+βnxn+γnTxn
其中,{αn},{βn},{γn},{εn}为(0,1)中的实数序列,αn+βn+γn= ,则{xn}有界,且强收敛于T 的不动点.
,则{xn}有界,且强收敛于T 的不动点.
设C 是Banach 空间中的非空闭凸子集,参数族Γ={T(s)∶s ∈R+}被称为非扩张半群,若满足以下条件:
(ⅰ)T(0)x=x,∀x ∈C;
(ⅱ)T(s+t)=T(s)T(t),∀s,t ∈R+;
(ⅲ)‖T(s)x-T(s)y‖≤‖x-y‖,∀x,y ∈C,s ≥0;
(ⅳ)∀x ∈C,映射T(·)x∶R+→C 是连续的.
F(Γ)表示Γ 的不动点集,即F(Γ)={x ∈C,T(s)x=x,0≤x < ∞}.
设C 是Hilbert 空间中的非空闭凸子集.参数族Γ={T(t)∶t ∈R+}被称为Lipschitz 映射的强连续半群,若满足以下条件:
(ⅰ)T(0)x=x,∀x ∈C;
(ⅱ)T(s+t)=T(s)T(t),∀s,t ∈R+;
(ⅲ)∀t>0,存在一个有界测度函数Lt∶(0,+∞)→[0,+∞)使得
‖T(t)x-T(t)y‖≤Lt‖x-y‖,∀x,y ∈C;
(ⅳ)∀x ∈C,映射T(·)x∶R+→C,若Lt=1,Lipschitz 映射的强连续半群被称为非扩张映射的强连续半群.
若![]() supLt≤1,则称它是渐近非扩张映射的强连续半群.
supLt≤1,则称它是渐近非扩张映射的强连续半群.
若存在x0使得T(t)x0=x0,∀t ≥0,称Γ 有一个不动点.F(Γ)表示Γ 的不动点集,即F(Γ)=∩t∈R+F(T(t)).
定理4 设C 为实Banach 空间E 的非空闭凸子集,T∶C→C 为非扩张映射,f∶C→C 为具有系数ρ 的压缩映射.如果定义算子:
其中t ∈(0,1),n ≥0,![]() =∞,则Tt,n是压缩的,且Tt,n的不动点列强收敛到T 的不动点.
=∞,则Tt,n是压缩的,且Tt,n的不动点列强收敛到T 的不动点.
定理5 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.Γ={T(s)∶s ∈R+}为非扩张半群,且F(T)≠ϕ.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理4 所定义的压缩映射.如果实数序列{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足下列条件:
则由得到的序列
{xn}有界,且强收敛于T 的不动点p,其中p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C.
定理6 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.Γ={T(s)∶s ∈R+}为非扩张半群,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理4 所定义的压缩映射.如果实数序列{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足下列条件:
则由得到的序列
{xn}有界,且强收敛于T 的不动点p,其中p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C.
定理7 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.Γ={T(s)∶s ∈R+}为非扩张半群,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理4 所定义的压缩映射.如果实数序列{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足下列条件:
则由得到的序列
{xn}有界,且强收敛于T 的不动点p,其中p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C.
引理6 设C 为实Banach 空间E 的非空闭凸子集,T∶C→C 为非扩张映射,f∶C→C 为具有系数ρ 的压缩映射.如果定义算子:
Tt,nx=(1-γn-tβn)u+(1-αn)tf(x)+(1-t)γnTx.
其中t ∈(0,1),n ≥0,αn+βn+γn=1,则Tt,n是压缩的,且Tt,n的不动点列强收敛到T 的不动点.
证明 设∀x,y ∈C,由f 的压缩性以及T 的非扩张性,得
因为ρ ∈(0,1),所以0 < γn+tρβn< 1,即Tt,n为压缩映射.由Banach压缩映象原理可知,Tt,n存在唯一的不动点,记作pt,n,即
由引理1,得![]() =pn∈F(T).若假设存在另一个不动点pm,且
=pn∈F(T).若假设存在另一个不动点pm,且![]() =pm,则pn,pm均是距f 的不动点最近的点.因此pn=pm=p ∈F(T),所以
=pm,则pn,pm均是距f 的不动点最近的点.因此pn=pm=p ∈F(T),所以![]() pt,n=p ∈F(T).
pt,n=p ∈F(T).
定理8 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.T∶C→C 为非扩张映射,且F(T)≠ϕ.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由引理5 所定义的压缩映射.如果实数序列{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足下列条件:
则由得到的序列
{xn}有界,且强收敛于T 的不动点p,其中p 是满足如下变分不等式的唯一解:
〈p-f(p),x-p〉 ≥0,∀x ∈C.
定理9 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E 的非空闭凸子集.T∶C→C 为非扩张映射,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由引理5 所定义的压缩映射.如果定义序列
xn+1=αnf(xn)+βnxn+γnTxn
其中{αn},{βn},{γn},{εn}为(0,1)中的实数序列,αn+βn+γn= ,则{xn}有界,且强收敛于T 的不动点.
,则{xn}有界,且强收敛于T 的不动点.
若在定理3 或定理9 中令f ≡u 为一常数函数,则有如下的结论:
定理10 设E 为具有一致Gateaux 可微范数的实Banach 空间,C 为E的非空闭凸子集.T∶C→C 为非扩张映射,且F(T)≠∅.设f∶C→C 为具有系数ρ 的压缩映射,Tt,n由定理2 或者引理5 所定义的压缩映射.如果定义序列
xn+1=αnu+βnxn+γnTxn
其中{αn},{βn},{γn},{εn}为(0,1)中的实数序列,αn+βn+γn=1,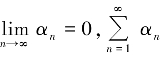 =∞,则{xn}有界,且强收敛于T 的不动点.
=∞,则{xn}有界,且强收敛于T 的不动点.
引理7 设{xn},{yn}是Banach 空间E 中的有界序列,{βn}是[0,1]中的序列,且![]() < 1.假设xn+1=βnyn+(1 -βn)xn,n ≥0,若
< 1.假设xn+1=βnyn+(1 -βn)xn,n ≥0,若![]() sup(‖yn+1-yn‖-‖xn+1-xn‖)≤0,则
sup(‖yn+1-yn‖-‖xn+1-xn‖)≤0,则![]() ‖yn-xn‖=0.
‖yn-xn‖=0.
设C 为E 的非空闭凸子集,T∶C→C 为渐近非扩张映射,f∶C→C 为具有压缩系数ρ 的压缩映射.若定义
Tmum=(1-αm)T(tm)um+αmf(um)
其中tm∈R+,m>0.则有如下的结论:
引理8 设C 为具有一致Gateaux 可微范数的自反严格凸的实Banach空间E 的非空闭凸子集,Γ={T(t)∶t ∈R+}为具有Lipschitz 系数{Lt}⊂[1,∞)的渐近非扩张映射的强连续半群,f∶C→C 为具有压缩系数ρ 的压缩映射.假设F(Γ)≠∅,算子Tm由上式所定义,其中αm⊂(0,1),Ltm-1 <αm,tm∈R+,且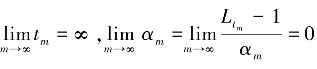 ,则∀m ≥0 时Tm是压缩的.
,则∀m ≥0 时Tm是压缩的.
证明 设∀{um},{vm}∈C,由f 的压缩性以及T 的渐近非扩张性,可得
因为Ltm-1 < αm,0 < ρ < 1,所以Ltm(1 -αm)+ραm< 1+αm(ρ -1)< 1,所以Tm为压缩映射.
由Banach 压缩映象原理可知Tm有唯一的不动点um,使得Tmum=um,即
um=Tmum=(1-αm)T(tm)um+αmf(um)
利用文献[51]中定理3.1 的证明方法可知um强收敛于F(Γ)的一个点,记为点p,即um→p ∈F(Γ).
定理11 设C 为具有一致Gateaux 可微范数的自反严格凸的实Banach 空间E 的非空闭凸子集,Γ={T(t)∶t ∈R+}为具有Lipschitz 系数{Lt}⊂[1,∞)的渐近非扩张映射的强连续半群,f∶C→C 为具有压缩系数ρ 的压缩映射.假设F(Γ)≠∅,算子Tn由上式所定义,序列{xn},{yn}由
所定义,其中{αn},{βn},{γn},{εn}为(0,1)中的实数序列,且满足
假设{T(tn)}是一致渐近规则的,则{xn}有界,且强收敛于F(Γ)的一个点.
证明 设p ∈F(Γ),由T 的渐近非扩张性得
对于∀n ≥0,由f 的压缩性以及T 的渐近非扩张性,有
记M1=max{‖x0-p‖,d‖f(p)-p‖},其中d=(1-ρ -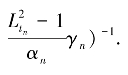 可见‖xn-p‖≤M1,所以{xn}有界,进一步可得{yn},{f(xn)},{T(tn)xn},{T(tn)yn}均有界.
可见‖xn-p‖≤M1,所以{xn}有界,进一步可得{yn},{f(xn)},{T(tn)xn},{T(tn)yn}均有界.
从而
令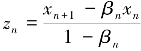 ,则
,则
由于{T(t)∶t ∈R+}是一致渐近规则的,且![]() ,所以
,所以
‖xn-T(tn)xn‖≤‖xn-xn+1‖+‖xn+1-T(tn)xn‖→0.
进而,对∀t ∈R+,有
另一方面,由引理2 可知
若记M2=sup‖xn-p‖2,整理上式得
由引理5,不妨设um为Tm的唯一不动点.于是
um-xn=αm(f(um)-xn)+(1-αm)[T(tm)um-xn]
所以
其中M3=sup{‖xn-T(tm)xn‖+2Ltm‖xn-um‖,n ≥0}.因此
由条件(ⅱ)可得
又![]() =p,所以
=p,所以![]() sup〈f(p)-p,j(xn-p)〉≤0 记λn=
sup〈f(p)-p,j(xn-p)〉≤0 记λn= αn,则由引理4 可知,
αn,则由引理4 可知,![]() ‖xn-p‖=0,即数列{xn}强收敛于F(Γ)的一个点p ∈F(Γ).
‖xn-p‖=0,即数列{xn}强收敛于F(Γ)的一个点p ∈F(Γ).
设μ 是l∞上满足‖μ‖=1=μ(1)的连续线性泛函,则μ 是N 上的均值当且仅当
inf{an;n ∈N}≤μ(a)≤sup{an;n ∈N},∀a=(a1,a2,…)∈l∞.
如果以μn(an)代替μ(a),并且满足μn(an)=μn(an+1),则称均值μn为Banach 极限.
定义映射φ(y)=μn‖xn-y‖2,∀y ∈E,则φ(y)是连续凸的且φ(y)→∞(‖y‖→∞).若E 是自反的,则存在z ∈C 使得φ(z)=![]() φ(y)(见文献[5]、[12]).因此
φ(y)(见文献[5]、[12]).因此
显然,Cmin是E 的闭凸子集.
引理9 设E 是具有一致Gateaux 可微范数的实Banach 空间,C 是E 的非空闭凸子集.设{xn}是E 中的有界序列,μn是Banach 极限且z ∈C.则
等价于
μn〈y-z,J(xn-z)〉≤0,∀y ∈C.
引理10 设α 是一实数,(x0,x1,…)∈l∞且对Banach 极限满足μn(xn)≤α.若![]() sup(xn+1-xn)≤0,则
sup(xn+1-xn)≤0,则![]() sup xn≤α.
sup xn≤α.
引理11 设{an}为一非负实数序列且满足以下条件:
an+1≤(1-θn)an+σn,n ≥0,
其中{θn}是(0,1)中的序列且{σn}是实数列使得
则![]() =0.
=0.
Takahashi 为了研究有限族非扩张的强收敛定理及其应用问题,引入了Wn映射的定义:
其中{Ti,i=1,2,…,N}是非扩张映射,由Takahashi[34] 可知,Wn是非扩张的并且![]() .
.
定理12 设E 是对偶E∗的光滑的严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一族非扩张映射,映射Wn由(1)定义使得F=Cmin∩F(Wn)≠∅,f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射.设{xn},{yn},{zn}由
所定义,{αn},{βn},{γn},{λn},{εn}为(0,1)中的实数列,且满足
则序列{xn}强收敛于{Ti∶C→C,i=1,2,…,N}的公共不动点p,其中p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的唯一解.
证明 由于{Ti,i=1,2,…,N}是非扩张映射,由Takahashi[8] 可知,Wn是非扩张的并且![]() .设p ∈F,由Wn的非扩张性,可知
.设p ∈F,由Wn的非扩张性,可知
对于∀n ≥0,由Wn的非扩张性和f 的压缩性,可知
记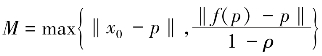 ,则‖xn-p‖≤M,所以{xn}有界,进一步可得{yn},{zn},{Wnxn},{Wnyn},{f(xn)}均有界.(www.chuimin.cn)
,则‖xn-p‖≤M,所以{xn}有界,进一步可得{yn},{zn},{Wnxn},{Wnyn},{f(xn)}均有界.(www.chuimin.cn)
下面将说明‖xn+1-xn‖→0.
令xn+1=βnxn+(1-βn)wn,则有
且
‖Wn+1yn+1-Wnyn‖≤‖yn+1-yn‖+‖Wn+1yn-Wnyn‖.
又因为yn=εnxn+(1-εn)Wnzn,所以有
同时
‖xn-Wnzn‖≤‖xn-Wnxn‖+‖Wnxn-Wnzn‖.
故可得
又因为Ti和Un,m都是非扩张映射,从而可得
其中,M1=max{‖xn‖,![]() ‖TN-iUn,N-(i+1)xn‖}.
‖TN-iUn,N-(i+1)xn‖}.
令vn=Un,N-1xn,vn+1=Un+1,N-1xn,则有
进而有
因此则有
同理可得
其中L1=max{‖yn‖,![]() ‖TN-iUn,N-(i+1)yn‖}.
‖TN-iUn,N-(i+1)yn‖}.
其中L2=max{![]() }.从而由条件(ⅰ),(ⅱ)和(ⅲ),得
}.从而由条件(ⅰ),(ⅱ)和(ⅲ),得
由引理7 得![]() sup‖wn-xn‖=0,因此有
sup‖wn-xn‖=0,因此有
‖xn+1-xn‖=| 1-βn| ‖wn-xn‖→0.
最后将说明{xn}强收敛于p ∈F.
由于p ∈F=Cmin∩F(Wn),由Cmin的定义,可知μn‖xn-p‖2=![]() ,再由引理1 可得
,再由引理1 可得
μn〈f(p)-p,j(xn-p)〉≤0.
由于J 是弱一致连续的对偶映象,从而可得
故序列{〈f(p)-p,j(xn-p)〉}满足引理10 的条件.因此必有
另一方面,由引理4 可知
若记M2=sup‖xn-p‖2,整理上式得
令 ,由于{xn}是有界的,由以及条件(ⅰ)再根据引理11,可得
,由于{xn}是有界的,由以及条件(ⅰ)再根据引理11,可得![]() ‖xn-p‖=0,即序列{xn}强收敛于Ti∶C→C,i=1,2,…,N 的公共不动点p,可知p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的解.
‖xn-p‖=0,即序列{xn}强收敛于Ti∶C→C,i=1,2,…,N 的公共不动点p,可知p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的解.
下面说明p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的唯一解.假设 ∈F 是该变分不等式的另一解,则有
∈F 是该变分不等式的另一解,则有
将两式相加,可得‖p- ‖2≤ρ‖p-
‖2≤ρ‖p- ‖2,0 < ρ < 1,所以p=
‖2,0 < ρ < 1,所以p=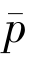 ,即变分不等式解的唯一性得证.
,即变分不等式解的唯一性得证.
定理13 设E 是具有对偶E∗的光滑的严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一族非扩张映射,映射Wn由(1)定义使得F=Cmin∩F(Wn)≠∅,f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射.如果定义序列
xn+1=αnf(xn)+βnxn+γnWnxn,
其中{αn},{βn},{γn}为(0,1)中的实数列,且满足
则序列{xn}强收敛于{Ti∶C→C,i=1,2,…,N}的公共不动点p,其中p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的唯一解.
定理14 设E 是具有对偶E∗的光滑的严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一族非扩张映射,映射Wn由(1)定义使得F=Cmin∩F(Wn)≠∅,f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射.如果定义序列
其中{αn},{βn},{γn},{εn}为(0,1)中的实数列,且满足
则序列{xn}强收敛于{Ti∶C→C,i=1,2,…,N}的公共不动点p,其中p 是变分不等式〈f(p)-p,j(y-p)〉≤0,∀y ∈F 的唯一解.
证明 由于{Ti,i=1,2,…,N}是非扩张映射,由Takahashi 可知,Wn是非扩张的并且![]() .设p ∈F,由Wn的非扩张性,可知
.设p ∈F,由Wn的非扩张性,可知
‖yn-p‖=‖εnxn+(1-εn)Wnxn-p‖≤‖xn-p‖.
对于∀n ≥0,由f 的压缩性,可知
记M=max{‖x0-p‖,![]() },则‖xn-p‖≤M,所以{xn}有界,进一步可得{yn},{Wnxn},{Wnyn},{f(xn)}均有界.
},则‖xn-p‖≤M,所以{xn}有界,进一步可得{yn},{Wnxn},{Wnyn},{f(xn)}均有界.
令xn+1=βnxn+(1-βn)wn,则有
又因为yn=εnxn+(1-εn)Wnxn,所以有
可得
再类似于定理13,得证.
定理15 设E 是具有对偶E∗的光滑的严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.设Tn∶C→C 是一族非扩张映射使得F=∩n≥1F(Tn)(nmodN)≠∅.设Q∶C→F 是一个阳光非扩张的,f∶C→C 是具有压缩因子ρ ∈(0,1)的压缩映射.若序列{xn}由x1∈C 迭代产生
xn+1=αnf(xn)+βnxn+γnTnxn
其中序列{xn}满足条件(C),{αn},{βn},{γn}是[0,1] 中的非负实数列[0,1],且
则序列xn强收敛于 =Q(f(
=Q(f(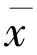 ))∈F 且
))∈F 且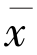 是如下变分不等式的唯一解
是如下变分不等式的唯一解
证明 首先说明{xn}是有界的.不妨取p ∈F,由于Tn(nmodN)是非扩张的,因此有
‖Tnxn-p‖=‖Tnxn-Tnp‖≤‖xn-p‖.
对于∀n ≥0,根据映射Tn和f 的映射,有
因此,{xn}是有界的,从而可得{Tnxn}和{f(xn)}也有界.
因为![]() ,所以‖xn+1-Tnxn‖.因为序列{xn}是有界的,所以存在{xn}的子序列{xnk}和w ∈C 使得xnk→w,又因为{xn}满足条件(C),所以w ∈F.
,所以‖xn+1-Tnxn‖.因为序列{xn}是有界的,所以存在{xn}的子序列{xnk}和w ∈C 使得xnk→w,又因为{xn}满足条件(C),所以w ∈F.
因为Q 是阳光非扩张的,f 是压缩映射,所以Q(f)是压缩的,故Q(f)有唯一的不动点,且Q(f)的不动点正是f 的不动点.若令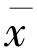 是f 的不动点,则有
是f 的不动点,则有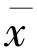 =f(
=f( )=Q(f(
)=Q(f( ))∈F,因为J(x)是弱连续的,所以有
))∈F,因为J(x)是弱连续的,所以有
同时
令M3=sup‖xn- ‖2,则有
‖2,则有
其中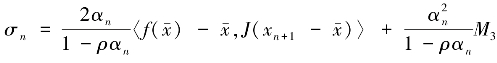 .若令λn=
.若令λn=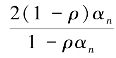 则可推出
则可推出![]() =0,即序列{xn}强收敛于Tn的公共不动点.
=0,即序列{xn}强收敛于Tn的公共不动点.
根据Q 的性质以及上面的推导可知, 是变分不等式的解.下面将说明它是变分不等式的唯一解.
是变分不等式的解.下面将说明它是变分不等式的唯一解.
假设 ∈F 是变分不等式的另一个解.因为
∈F 是变分不等式的另一个解.因为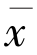 也是变分不等式的解,所以〈f(
也是变分不等式的解,所以〈f(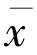 )-
)- ,j(y-
,j(y- )〉≤0,∀y ∈F.同时有
)〉≤0,∀y ∈F.同时有
另一方面,对于 ∈F,因为
∈F,因为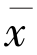 ∈F,所以
∈F,所以
将这两式相加,可得
即
因此
因为ρ ∈(0,1)所以可推出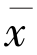 =
=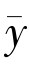 ,解的唯一性获证.
,解的唯一性获证.
若在定理15 中,令f ≡u 为一个常数函数,则有下面的推论:
推论 设E 是具有对偶E∗的光滑的严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.设Tn∶C→C 是一族非扩张映射使得F=∩n≥1F(Tn)(nmodN)≠∅.设Q∶C→F 是一个阳光非扩张的,f ≡u ∈C 为常数函数.若序列{xn}由x1∈C 迭代产生
xn+1=αnu+βnxn+γnTnxn
其中序列{xn}满足条件(C),{αn},{βn},{γn}是[0,1] 中的非负实数列[0,1],且
则序列xn强收敛于 =Q(f(
=Q(f( ))∈F 且
))∈F 且 是如下变分不等式的唯一解
是如下变分不等式的唯一解
定理16 设E 为实自反Banach 空间,有弱连续的对偶映射J,C 为E 的非空闭凸子集.Tn∶C→C 为一族非扩张映射,F=∩n≥1F(Tn)≠∅为C 的单面非扩张收缩,Q 为单面非扩张收缩,f∶C→C 为具有系数ρ 的压缩映射.设{xn},{yn}由下式所定义
且{xn}满足条件(A).设{αn},{βn},{γn}为(0,1)中的实数列,且满足
则{xn}有界,且强收敛于Tn的公共不动点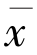 =Q(f(
=Q(f(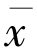 )),其中
)),其中 是变分不等式〈f(
是变分不等式〈f( )-
)-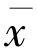 ,j(y-
,j(y- )〉≤0,∀y ∈F 的唯一解.
)〉≤0,∀y ∈F 的唯一解.
证明 设p ∈F,由Tn的非扩张性,可知
对于∀≥0n,由Tn的非扩张性和f 的压缩性,可知
记 ,则‖xn-p‖≤M,所以{xn}有界.进一步可得{yn},{Tnxn},{Tnyn},{f(xn)}均有界.由于{xn}满足条件(A),所以‖xn+1-Tnxn‖→0.由于E 是自反的,{xn}是有界的,所以存在{xn}的子序列{xnk}使得{xnk}弱收敛到w.由于{xn}满足条件(A),所以w ∈F.
,则‖xn-p‖≤M,所以{xn}有界.进一步可得{yn},{Tnxn},{Tnyn},{f(xn)}均有界.由于{xn}满足条件(A),所以‖xn+1-Tnxn‖→0.由于E 是自反的,{xn}是有界的,所以存在{xn}的子序列{xnk}使得{xnk}弱收敛到w.由于{xn}满足条件(A),所以w ∈F.
设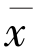 =Q(f(
=Q(f(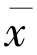 )),由于J(x)是弱连续的,Q 为单面非扩张收缩,利用引理1 可知
)),由于J(x)是弱连续的,Q 为单面非扩张收缩,利用引理1 可知
另一方面,由引理3 可知
若记M2=sup‖xn- ‖2,整理上式,则可得
‖2,整理上式,则可得
令 因为
因为![]() ≤0,同时利用引理2,可知
≤0,同时利用引理2,可知![]() =0,即数列{xn}强收敛于Tn的公共不动点.由Q的性质可知,
=0,即数列{xn}强收敛于Tn的公共不动点.由Q的性质可知, 是变分不等式〈f(
是变分不等式〈f(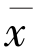 )-
)- ,j(y-
,j(y- )〉≤0 的解.假设
)〉≤0 的解.假设 ∈F 是该变分不等式的另一解,则有
∈F 是该变分不等式的另一解,则有
将两式相加,可得 =
= ,即
,即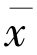 的唯一性得证.
的唯一性得证.
定理17 设E 为具有一致Gateaux 可微范数的Banach 空间,K 为E 的一个非空闭凸子集,T∶K→K 为非扩张映射且F(T)∩Kmin≠∅.如果αn,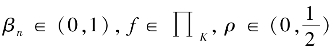 ,并满足下列条件:
,并满足下列条件:
则由式
定义的迭代序列{xn}有界,且{xn}强收敛于T 的某个不动点p.
证明 设p ∈F(T)∩Kmin,由T 的非扩张性得
记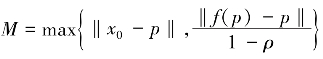 ,由数学归纳法得‖xn-p‖≤M,即{xn}为有界序列.
,由数学归纳法得‖xn-p‖≤M,即{xn}为有界序列.
由于![]() 和p=Tp,则由引理1 得
和p=Tp,则由引理1 得
μn〈f(p)-p,J(xn-p)〉≤0.
又因为正规对偶映像J∶E→2E∗在具有一致Gateaux 可微范数的Banach 空间E 上是单值的,且在E 的任意有界子集上由E 的范数拓扑到E∗的弱∗拓扑是一致连续的,则由(ⅱ)可得
即序列{〈f(p)-p,J(xn-p)〉}满足引理2 中的条件,所以
另一方面,因为f ∈∏K,且压缩系数![]() ,由引理3 得
,由引理3 得
整理上式得
取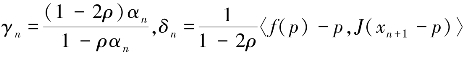 ,由(ⅰ)可得γn∈(0,1)且
,由(ⅰ)可得γn∈(0,1)且
由引理5 得![]() ‖xn-p‖=0,即序列{xn}强收敛于不动点p ∈F(T).
‖xn-p‖=0,即序列{xn}强收敛于不动点p ∈F(T).
定理18 设E 为具有一致Gateaux 可微范数的Banach 空间,K 为E 的一个非空闭凸子集,T∶K→K 为非扩张映射且F(T)∩Kmin≠∅.如果αn,βn∈(0,1),f ∈∏K,并满足下列条件:
则由式
定义的迭代序列{xn}有界,且{xn}强收敛于T 的某个不动点p.
证明 设p ∈F(T)∩Kmin,由式(4)得
可得‖xn-p‖≤M,即{xn}为有界序列.
另一方面,因为f ∈∏K,压缩系数ρ ∈(0,1),由引理3 得
记![]() ,并整理上式得
,并整理上式得
取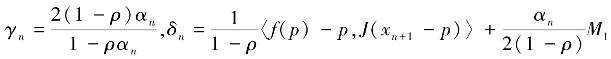 ,由(ⅰ)得
,由(ⅰ)得
因此![]() ‖xn-p‖=0,即序列{xn}强收敛于不动点p ∈F(T).
‖xn-p‖=0,即序列{xn}强收敛于不动点p ∈F(T).
定理19 设E 为具有一致Gateaux 可微范数的Banach 空间,K 为E 的一个非空闭凸子集,T∶K→K 为非扩张映射且F(T)∩Kmin≠∅.如果αn,βn∈(0,1),f ∈∏K,并满足下列条件:
则由式
定义的迭代序列{xn}有界,且{xn}强收敛于T 的某个不动点p.
证明 由定理18得{xn},{f(xn)},{Txn}有界.记M2≥max{‖f(xn)-xn‖,‖Txn-xn‖,‖xn-p‖},则
‖xn+1-xn‖≤αn‖f(xn)-xn‖+(1 -αn)βn‖Txn-xn‖≤(αn+βn)M2,
由(ⅰ)和![]() 可得
可得![]() ‖xn+1-xn‖=0.由定理2 得{xn}强收敛于不动点p ∈F(T).
‖xn+1-xn‖=0.由定理2 得{xn}强收敛于不动点p ∈F(T).
另一方面,如果![]() βn< 1,令γn=(1 -αn)βn,n ≥0,并定义xn+1=γnxn+(1-γn)zn,则
βn< 1,令γn=(1 -αn)βn,n ≥0,并定义xn+1=γnxn+(1-γn)zn,则
由T 的非扩张性得
由(ⅰ)及{f(xn)},{Txn}的有界性,得
由引理4 得![]() ‖zn-xn‖=0.又因为xn+1-xn=(1-γn)(zn-xn),所以
‖zn-xn‖=0.又因为xn+1-xn=(1-γn)(zn-xn),所以![]() ‖xn+1-xn‖=0.由定理2 得{xn}强收敛于不动点p ∈F(T).
‖xn+1-xn‖=0.由定理2 得{xn}强收敛于不动点p ∈F(T).
定理20 设E 为具有一致Gateaux 可微范数的实Banach 空间,E∗为E的对偶空间,K 为E 的一个非空闭凸子集,T1,T2,…,TN∶K→K 为非扩张映象且F ∩Kmin≠∅.如果αn,βn∈(0,1),f ∈∏K,并满足下列条件:
则由式
定义的迭代序列{xn}强收敛到T1,T2,…,TN的某个公共不动点p.
证明 首先,证明序列{xn}有界.设p ∈F ∩Kmin,则
类似地,递推可得
因此{xn}有界,进一步可得{f(xn)}和{Wnxn}有界.
其次,证明![]() ‖xn+1-xn‖=0.令γn=(1-αn)βn,n ≥0,则由(ⅰ)和(ⅱ)得
‖xn+1-xn‖=0.令γn=(1-αn)βn,n ≥0,则由(ⅰ)和(ⅱ)得
如果定义xn+1=γnxn+(1-γn)zn,则得
由此可得
因为Ti和Un,N为非扩张映象,则得
其中常数![]() ,n ≥1},并且
,n ≥1},并且
因此,有
得
得
由条件(ⅰ)αn→0 和(ⅲ)![]() =0,得
=0,得
由引理3 得
并且
最后,证明{xn}强收敛到p ∈F.因为![]() 和p=Tp,由引理1 得
和p=Tp,由引理1 得
μn〈f(p)-p,J(xn-p)〉≤0.
由于正规对偶映象J∶E→2E∗在一致Gateaux 可微范数的Banach 空间E 上是单值的,且在E 的任意有界子集上由E 的范数拓扑到E∗的弱拓扑是一致连续的,则由(11)得
即序列{〈f(p)-p,J(xn-p)〉}满足引理2 中的条件,所以
另一方面,由于f ∈∏K,且压缩系数ρ ∈(0,1),由引理4 得
整理可得(不妨记![]()
其中 .由
.由
(ⅰ)得
由引理5 得
即序列{xn}强收敛于不动点p ∈F(T).
定理21 设E 为具有一致Gateaux 可微范数的实Banach 空间,E∗为E的对偶空间,K 为E 的一个非空闭凸子集,T1,T2,…,TN∶K→K 为非扩张映象且F ∩Kmin≠∅.如果αn,βn∈(0,1),f ∈∏K,并满足下列条件:
则由定理20 定义的迭代序列{xn}强收敛到T1,T2,…,TN的某个公共不动点p.
定理22 设E 为具有一致Gateaux 可微范数的实Banach 空间,E∗为E的对偶空间,K 为E 的一个非空闭凸子集,T∶K→K 为非扩张映象且F(T)∩Kmin≠∅.如果αn,βn∈(0,1),f ∈∏K,并满足下列条件:
则由式定理20 定义的迭代序列{xn}强收敛到T 的某个不动点p.
有关不动点与零点的迭代逼近及应用的文章

布劳威尔不动点定理是代数拓扑的早期成就,还是更一般的不动点定理的基础,在泛函分析中尤其重要.1904年,首先由Piers Bohl 证明n=3 的情况(发表于《纯粹及应用数学期刊》 之内).1909年,鲁伊兹·布劳威尔(L.E.Brouwer)再次证明.1910年,雅克·阿达马提供一般情况的证明,而布劳威尔在1912年提出另一个不同的证明.这些早期的证明皆属于非构造性的间接证明,与数学直觉主义理想......
2023-10-20

变分不等式是非线性互补问题的推广,它的提出统一了优化问题和均衡问题的研究,并且在数学领域内作为大量数学问题实际求解的统一框架.变分不等式广泛应用于工程优化,经济学和交通运输的平衡问题,对数学各个领域、计算机科学等方面都产生了巨大的影响.经典变分问题的推广和发展,将经典变分问题的约束条件放松为某些单边约束(即用不等式代替等式)的变分方法.它是研究偏微分方程、最佳控制和其他领域的一个十分有用的工具,也......
2023-10-20

设X 和Y 是两个线性赋范空间,其范数为‖·‖X 和‖·‖Y.令V,W分别是X,Y 的子集,F:V→W 是一映射.(ⅰ)直接问题是指由x∈V 来确定y=F(x),(即,由起因得出结论);(ⅱ)反问题是对任意的y∈W 通过y=F(x)来决定x∈V,(即,由结论推出起因);(ⅲ)映射F 被称为直接映射.关于反问题(也称逆问题)的研究,早期的工作可追溯到20 世纪20年代美国的Hadamard 教授在研......
2023-10-20

数学里到处要解方程,诸如代数方程、函数方程、微分方程等,种类繁多,形式各异.但是它们常能改写成f(x)=x 的形状,这里x 是某个适当的空间X 中的点,f 是从X 到X 的一个映射或运动.把每一点x 移到点f(x),方程f(x)=x 的解恰好就是在f 这个运动之下被留在原地不动的点,故称不动点.即这个函数映射到其自身一个点.于是,解方程的问题就转化成了找不动点这个几何问题.不动点问题实际上就是各种......
2023-10-20

分裂可行问题Split Feasibility Problem(SEP)是由Censor 和Elfving 在1994 首先提出的,该问题描述如下:寻找一个点x使得其中C 和Q 分别是Hilbert 空间H1和H2的非空闭凸子集,A 是由H1到H2的有界线性算子.在过去20年,许多学者都对分裂可行问题的数值逼近进行了研究提出了若干算法,比如Byrne 展示了他们的CQ 算法,杨庆之介绍了松弛CQ算......
2023-10-20

下面将给出几个关于第(1)类非扩张映象在Hilbert 空间上的定义和定理.定理1(Browder-Petryshyn)设H 是一个Hilbert 空间,C 为Hilbert 空间H 的非空有界闭凸子集.设T∶C→C 使第(1)类非扩张型映象,则T 在C中存在不动点.通常用F(T)来表示T 的不动点集,即F(T)={x ∈C∶Tx=x}.定理2(Browder)设X 是一致凸Banach 空间......
2023-10-20

除了前面两节介绍的在Hilbert 空间和Banach 空间中关于伪压缩映射的一些不动点定理之外,伪压缩映射的不动点定理还可以通过其他的方式来体现,比如通过空间的构造,利用投影的混合算法实现序列的收敛性等.称T 为渐近λ-严格伪压缩映象,如果存在常数λ ∈[0,1),使得称T 为渐近伪压缩映象,如果存在常数使得〈T nx-T ny,x-y〉≤kn‖x-y‖2,n ≥1,x,y ∈C.设H 为一实H......
2023-10-20

,cn)是依赖于参数c0,c1,…,cn的初等函数.用P(x,c0,c1,…,cn)来近似表示f,要求选择一组参数使误差最小.这就是寻求极小问题的解.当参数给出最小误差时,就把叫作f在P(x,c0,c1,…,cn)所构成的函数类中的一个最佳逼近元;数值P叫作f借助于函数P(x,c0,c1,…......
2023-10-20
相关推荐