数学里到处要解方程,诸如代数方程、函数方程、微分方程等,种类繁多,形式各异.但是它们常能改写成f(x)=x 的形状,这里x 是某个适当的空间X 中的点,f 是从X 到X 的一个映射或运动.把每一点x 移到点f(x),方程f(x)=x 的解恰好就是在f 这个运动之下被留在原地不动的点,故称不动点.即这个函数映射到其自身一个点.于是,解方程的问题就转化成了找不动点这个几何问题.不动点问题实际上就是各种......
2025-09-30
设(X,d)是一完备的度量空间,T 是X 的自映像.T 称为非扩张映象(以后称为第(1)类非扩张型映象),如果
d(Tx,Ty)≤d(x,y)∀x,y ∈X.
非扩张映象是Banach 压缩映象的一种自然的推广,这种映象在近代许多数学分支,其中特别是在非线性半群、遍历理论和单调算子理论有许多重要的应用.一般说来,非扩张映象不一定存在不动点,所以下面将介绍非扩张映象不动点的存在性.先介绍非扩张型映象的分类.值得注意的是,若非扩张映象T∶X→X 有不动点,则它未必是唯一的(如恒等映射)并且由xn+1=Txn定义的序列{xn}也可能不强收敛于T 的不动点.
设(X,d)是一完备的度量空间,T 是X 的自映象.如果满足下面的一条件(m),m=1,2,…,5 则称T 是属于第(m)类的非扩张型映象.
其中a,b,c ≥0,且a+2b+2c≤1.
或等价于
其中a,b,c 为x,y 的非负函数且a(x,y)+2[b(x,y)+c(x,y)]≤1.![]()
第(1)类非扩张型映像为通常的非扩张映像,第(2)类非扩张型映像为Kannan 型非扩张映象.这两类映象分别是第(3)类映象当b=c=0,a≤1 和a=c=0,b≤时的特例.第(3)类和第(4)类非扩张映象有时称为平均非扩张映象.显然第(1)类映象至第(4)类映象都是第(5)类映象的特例.
对于第(1)类非扩张型映象,记C 为Hilbert 空间H 的非空子集,‖·‖表示范数,则有如下的定义:
若映射T∶C→C 满足条件
‖Tx-Ty‖≤‖x-y‖,∀x,y ∈C,
则称T 为非扩张的映射.
若映射T∶C→C 满足条件
‖Tx-Ty‖2≤‖x-y‖2-‖(I-T)x-(I-T)y‖2,∀x,y ∈C,
则称T 为严格非扩张的映射.
若映射T∶C→C 满足条件
F(T)≠∅,‖Tx-p‖≤‖x-p‖,∀x ∈C,p ∈F(T),
则称T 为拟非扩张的映射.
若映射T∶C→C 满足条件
2‖Tx-Ty‖2≤‖Tx-y‖2+‖Ty-x‖2,∀x,y ∈C,
则称T 为非传播的映射,即(https://www.chuimin.cn)
‖Tx-Ty‖2≤‖x-y‖2+2〈x-Tx,y-Ty〉,∀x,y ∈C.
若存在常数α ∈[0,1] 使得映射T∶C→C 满足条件
‖Tx -Ty‖2≤‖x -y‖2+α‖(I -T)x -(I -T)y‖2+2〈x -Tx,y -Ty〉,∀x,y ∈C,
则称T 为α 强伪非传播的映射.
称映射T∶C→C 是Lipschitz 连续的,若存在常数L>0 使得
‖Tx-Ty‖≤L‖x-y‖,∀x,y ∈C.
若映射T∶C→C 满足条件
‖Tx-Ty‖≤‖x-y‖,∀x ∈C,y ∈F(T),
则称T 为半非扩张映射.显然,若T 为非扩张的映射,则T 为半非扩张的映射,但逆命题并不成立.
设E 为一实Banach 空间,若E 中存在序列{xn}弱收敛到x,使得J(xn)依范数弱收敛到J(x),则称E 具有弱连续对偶映射.
设E 为一实Banach 空间,Tn∶C→C 为一族非扩张映射,{xn}弱收敛到x,且xn+1-Tnxn→0 时,x ∈(F),称{xn}满足条件(A).
设C 为Banach 空间E 的非空闭凸子集,T∶C→C,若![]() ‖x-Tx‖≤‖x -y‖,有‖Tx -Ty‖≤‖x -y‖,∀x,y ∈C,称T 满足条件(C).可见若T满足条件(C),则T是非扩张的.设C ⊆E 为有界凸的,Q∶E→C 为一映射.若Q(tx+(1 -t)Q(x))=Q(x),称Q 是单面的.若Q∶E→E,且Q2=Q,则称Q 是一个收缩.如果Q 是一个收缩,则有Q(z)=z,∀z ∈R(Q),其中R(Q)是Q 的值域.
‖x-Tx‖≤‖x -y‖,有‖Tx -Ty‖≤‖x -y‖,∀x,y ∈C,称T 满足条件(C).可见若T满足条件(C),则T是非扩张的.设C ⊆E 为有界凸的,Q∶E→C 为一映射.若Q(tx+(1 -t)Q(x))=Q(x),称Q 是单面的.若Q∶E→E,且Q2=Q,则称Q 是一个收缩.如果Q 是一个收缩,则有Q(z)=z,∀z ∈R(Q),其中R(Q)是Q 的值域.
若从E 到C 存在一个单面非扩张收缩,称C 为E 的单面非扩张收缩.
若Q∶C→F 是一个单面非扩张收缩,则F 是C 的单面非扩张收缩,又因为f 为压缩映射,从而Q(f)是压缩的.由Banach 压缩定理可知,Q(f)有唯一不动点,记作 ,即
,即 =Q(f(
=Q(f( )).
)).
设 (0,β)表示E 中以0 为心,β 为半径的闭球.定义一映象r∶X→
(0,β)表示E 中以0 为心,β 为半径的闭球.定义一映象r∶X→ 如下:
如下:
这一映象r 称为X 到 (0,β)上的保核收缩(映象).对于保核收缩映象,有如下的结果:
(0,β)上的保核收缩(映象).对于保核收缩映象,有如下的结果:
定理 设r 是X 到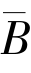 (0,β)上的保核收缩映象.
(0,β)上的保核收缩映象.
(ⅰ)如果X 是Hilbert 空间,则r 是第(1)类的非扩张映象.
(ⅱ)如果X 是Banach 空间,则r 是Lip 映象,更确切地说,r 满足下面的条件:
‖r(x)-r(y)‖≤2‖x-y‖,∀x,y ∈X.
相关文章

数学里到处要解方程,诸如代数方程、函数方程、微分方程等,种类繁多,形式各异.但是它们常能改写成f(x)=x 的形状,这里x 是某个适当的空间X 中的点,f 是从X 到X 的一个映射或运动.把每一点x 移到点f(x),方程f(x)=x 的解恰好就是在f 这个运动之下被留在原地不动的点,故称不动点.即这个函数映射到其自身一个点.于是,解方程的问题就转化成了找不动点这个几何问题.不动点问题实际上就是各种......
2025-09-30

,cn)是依赖于参数c0,c1,…,cn的初等函数.用P(x,c0,c1,…,cn)来近似表示f,要求选择一组参数使误差最小.这就是寻求极小问题的解.当参数给出最小误差时,就把叫作f在P(x,c0,c1,…,cn)所构成的函数类中的一个最佳逼近元;数值P叫作f借助于函数P(x,c0,c1,…......
2025-09-30

布劳威尔不动点定理是代数拓扑的早期成就,还是更一般的不动点定理的基础,在泛函分析中尤其重要.1904年,首先由Piers Bohl 证明n=3 的情况(发表于《纯粹及应用数学期刊》 之内).1909年,鲁伊兹·布劳威尔(L.E.Brouwer)再次证明.1910年,雅克·阿达马提供一般情况的证明,而布劳威尔在1912年提出另一个不同的证明.这些早期的证明皆属于非构造性的间接证明,与数学直觉主义理想......
2025-09-30

至今为止,世界上已有几十种用于成组技术的机械零件编码系统,应用最广的是奥匹兹分类编码系统。该系统是1964年西德Aachen 工业大学H.OPITZ 教授领导开发的,很多国家以它为基础建立了各自的分类编码系统,如日本的KK-3 系统以及我国的JLBM-1 系统。图9-2JLBM-1 分类编码系统编码示例回转类零件——锥套 材料:45 钢(锻件);非回转类零件——连接板 材料:HT150......
2025-09-29

E 为一实Banach 空间,E为E 的对偶空间,〈·,·〉表示广义对偶对,称J∶E→2E为正规对偶映象,如果Jx={f ∈E∶〈x,f 〉=‖x‖2=‖f ‖2},x ∈E.今后均用j 表示单值赋范对偶映射.设E 为一实Banach 空间,E为E 的对偶空间,C 为E 的一个闭凸子集.若S={x ∈E,‖x‖=1}为E 的单位球面,对任意的x,y ∈S,一致存在,则称E 的范数是一致Gateau......
2025-09-30

,N 是一族严格非扩张映射使得 假设α=inf{αi}>0,则存在非扩张映射Γ∶C→C 使得.证明设αi,i=1,2,…,N 是[0,1] 内的一组实数,且满足令由于Ti是非扩张的,所以由文献[20] 可知,Γ 是有意义的且这表明Γ 是非扩张的.下面将说明.......
2025-09-30

所谓的零件分类成组,就是按照一定的相似准则,将产品种类繁多的零件归并成为几个具有相似特征的零件族。零件分类成组方法目前可分为视检法、生产流程分析法和编码分类法。......
2025-09-29

1)西点的分类西点的分类标准目前尚未统一。按点心的温度分类,可分为常温点心、冷点心和热点心。按西点的用途分类,可分为零售类点心、酒会点心、自助餐点心、宴会点心和茶点。清酥类点心的口味有咸甜之分,是西点中常用的一类点心。该类点心口味清甜,适用于午餐、晚餐的餐后或非用餐时食用。2)西点的特点西点以其用料讲究、口感丰富、造型独特等众多优点,在西餐饮食中起着重要的作用。......
2025-09-29
相关推荐