不动点及零点的迭代逼近及应用

2023-10-20 理论教育版权反馈

【摘要】：除了前面两节介绍的在Hilbert 空间和Banach 空间中关于伪压缩映射的一些不动点定理之外,伪压缩映射的不动点定理还可以通过其他的方式来体现,比如通过空间的构造,利用投影的混合算法实现序列的收敛性等.称T 为渐近λ-严格伪压缩映象,如果存在常数λ ∈[0,1),使得称T 为渐近伪压缩映象,如果存在常数使得〈T nx-T ny,x-y〉≤kn‖x-y‖2,n ≥1,x,y ∈C.设H 为一实H

除了前面两节介绍的在Hilbert 空间和Banach 空间中关于伪压缩映射的一些不动点定理之外,伪压缩映射的不动点定理还可以通过其他的方式来体现,比如通过空间的构造,利用投影的混合算法实现序列的收敛性等.

称T 为渐近λ-严格伪压缩映象,如果存在常数λ ∈[0,1),使得

〈T nx-T ny,x-y〉≤kn‖x-y‖2,∀n ≥1,x,y ∈C.

设H 为一实Hilbert 空间,其内积和范数分别表示为〈·,·〉和‖·‖,C为H 的一个非空闭凸子集.以xn→x 和xn⇀x 分别表示序列{xn}强和弱收敛到x.对任意x ∈H,在C 中存在唯一的最近点PCx,即

‖x-PCx‖≤‖x-y‖,∀y ∈C,

称PC为H 到C 上的度量投影.从文献[53]可知,PC是非扩张的,且u=PCx的充分必要条件是

〈x-u,u-y〉 ≥0,∀y ∈C.

称T 是一致L-Lipschitz 连续的,如果存在L>0,使得

‖T nx-T ny‖≤L‖x-y‖,∀x,y ∈C,n ∈N.

引理1　设C 为Hilbert 空间H 的非空闭凸子集,T∶C→C 为渐近伪压缩映象.如果T 是一致L-Lipschitz 连续的,则Fix(T)为闭凸集.

引理2　设C 为Hilbert 空间H 的非空闭凸子集,T∶C→C 为渐近伪压缩映象.如果T 是一致L-Lipschitz 连续的,{xn}⊂C 且xn⇀x,xn-Txn→0,则x ∈Fix(T).

引理3　在Hilbert 空间H 中,下列不等式成立:

(ⅰ)‖x＋y‖2≤‖x‖2＋2〈y,(x＋y)〉,∀x,y ∈H;

(ⅱ)‖tx＋(1 -t)y‖2=t‖x‖2＋(1 -t)‖y‖2 -t(1 -t)‖x-y‖2,∀t ∈[0,1],∀x,y ∈H.

引理4　设C 为Hilbert 空间H 的非空闭凸子集,对任意x,y,z ∈H 和给定的a ∈R,则∏C为闭凸集,其中∏C={v ∈C∶‖y -v‖2≤‖x -v‖2＋〈z,v〉＋a}.

设(X,d)为一完备度量空间,称f∶X→X 为压缩映象:如果存在系数r ∈(0,1),使得

‖f(x)-f(y)‖≤r‖x-y‖,∀x,y ∈X.

Meir-Keeler 压缩映象:如果对任意ε>0,存在δ>0,当d(x,y)<ε＋δ 时,有

d(f(x),f(y))< ε,∀x,y ∈X.

Meir-Keeler 压缩映象包含压缩映象,是压缩映象的一种推广形式,且有如下结论:

引理5　设f 是完备度量空间(X,d)中的Meir-Keeler 压缩映象,则f 存在唯一不动点.

引理6　设K 为Banach 空间E 的凸子集,f∶K→K 为Meir-Keeler 压缩映象,则对任意ε>0,存在r ∈(0,1),当‖x-y‖ ≥ε 时,有‖f(x)-f(y)‖≤r‖x-y‖成立.

设{Cn}为H 的非空闭凸子集序列,N 为正整数集.如下定义H 的s-LinCn子集:x ∈s-LinCn当且仅当存在{xn}⊂H 并满足xn→x 和xn∈Cn,∀n ∈N.类似地,定义H 的w-LsnCn子集:y ∈w-LsnCn当且仅当存在{Cni}⊂{Cn},{yi}⊂H 并满足yi→y 和yi∈Cni,∀i ∈N.如果C0⊂H且C0=s-LinCn=w-LsnCn,称{Cn}收敛到C0,记为C0=M-limnCn.具有该极限性质最简单的例子是呈现包含关系的递减序列{Cn},比如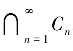 pagenumber_ebook=100,pagenumber_book=93 .

引理7　设{Cn}为Hilbert 空间H 的非空闭凸子集序列,如果C0=M-limnCn存在且不为空集,则对任意x ∈H,序列{PCnx}强收敛到{PC0x}.

定理1　设C 为Hilbert 空间H 的非空闭凸子集,f∶C→C 为Meir-Keeler 压缩映象,T∶C→C 为一致L-Lipschitz 连续的渐近伪压缩映象且Fix(T)≠∅.如果0 < a≤αn≤βn≤b 且对给定x1∈C,C1=C,则由式

定义的黏滞迭代序列{xn}强收敛到q ∈Fix(T),且q=PFix(T)f(q).

证明　由引理1 和PC的非扩张性,可知PFix(T)f 是定义在C 上的M eir-Keeler 压缩映象.由引理5,PFix(T)f 存在唯一不动点,记q=PFix(T)f(q).

首先,证明Cn是闭凸集且Fix(T)⊂Cn.由式(6)和引理4 易得Cn是闭凸集.

另一方面,由于Fix(T)⊂C1=C,不妨假设Fix(T)⊂Ck,k ≥1.对任意p ∈Fix(T)⊂Ck,得

因为

结合条件a≤αn≤βn≤b,得

其中θn=[qn(1＋(qn-1)βn)-1]M＋2(qn＋1)en,不难验证θn→0(n→∞).取n=k 即得p ∈Ck＋1.因此,对任意n ≥1,有Fix(T)⊂Cn＋1⊂Cn.

其次,证明=q.

因为是定义在C 上的Meir-Keeler 压缩映象,则存在唯一不动点设zn=PCnf(q),n ∈N,由于M-limnCn且Fix(T)⊂Cn＋1⊂Cn,则得

(反证法)如果xn→/ q,则有‖xn-q‖>0.设ε>0且sup‖xn-q‖>ε,由Meir-Keeler 压缩映象的定义,存在δ>0,sup‖xn-q‖>ε＋δ 且‖x-y‖ < ε＋δ 满足

‖f(x)-f(y)‖ < ε,x,y ∈C.(www.chuimin.cn)

另一方面,由引理6 可知,存在r ∈(0,1),当‖x-y‖≥ε＋δ 时,有

‖f(x)-f(y)‖ < r‖x-y‖,x,y ∈C.

考虑如下两种情形:(Ⅰ)存在n1>n0使得‖xn1-q‖ < ε＋δ,则得

‖xn1＋1-zn1＋1‖≤‖f(xn1)-f(q)‖ < ε,

进一步得

‖xn1＋1-q‖≤‖xn1＋1-zn1＋1‖＋‖zn1＋1-q‖ < ε＋δ.

这表明

(Ⅱ)对任意n ≥n0都有‖xn-q‖≥ε＋δ 成立,则得

‖f(xn)-f(q)‖ < r‖xn-q‖,n ≥n0.

进一步得

可得

在假设xn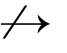 pagenumber_ebook=103,pagenumber_book=96 q 的条件下,由情形(Ⅰ)和(Ⅱ)分别得到两个相互矛盾的结论.因此=q.由于xn＋1=PCn＋1f(xn),所以

〈f(xn)-xn＋1,xn＋1-y〉 ≥0,∀y ∈Cn＋1.

又因为Fix(T)⊂Cn＋1,进一步得〈f(q)-q,q-y〉 ≥0,∀y ∈Fix(T),即q=PFix(T)f(q).

最后,证明q ∈Fix(T).既然xn→q(n→∞),则

得xn＋1∈Cn＋1⊂Cn,则

另一方面,因为

利用yn=(1-αn)xn＋αnT nzn可得

由于a≤αn≤βn≤b 且a>0,b ∈(0,L-2,存在正整数n0使得

整理得

取极限进一步得

又因为T 是一致L-Lipschitz 连续的,并且

所以得

因此得xn→q ∈Fix(T).

定理2　设C 为Hilbert 空间H 的非空闭凸子集,f∶C→C 为Meir-Keeler 压缩映象,T∶C→C 为一致L-Lipschitz 连续的渐近伪压缩映象且Fix(T)≠∅.如果0 < a≤αn≤βn≤b 且b ∈,对给定x1∈C,Q1=C,如下定义{xn}:

其中 θn=[qn(1＋ (qn-1)βn)-1]M＋ 2(qn＋ 1)en且M=sup{‖xn-p‖2∶p ∈Fix(T)}< ∞,则{xn}强收敛到q ∈Fix(T),且q=PFix(T)f(q).

证明　对任意n ≥1,Cn和Qn是H 的闭凸子集,且Fix(T)⊂Cn.由于x1∈C,Fix(T)⊂Q1=C,不妨假设xk∈C,Fix(T)⊂Qk.因为Fix(T)⊂Ck∩Qk,存在唯一的xk＋1=PCk∩Qkf(xk),所以

〈f(xk)-xk＋1,xk＋1-y〉 ≥0,∀y ∈Ck∩Qk.

进一步得〈f(xk)-xk＋1,xk＋1-y〉≥0,∀y ∈Fix(T),即Fix(T)⊂Qk＋1.因此,Fix(T)⊂Qn.

另一方面,由于是定义在C 上的Meir-Keeler 压缩映象,则存在唯一不动点设zn=PQnf(q),n ∈N,因为Fix(T)⊂Qn＋1⊂Qn,则由引理7 得zn→q=.又因为xn=PQnf(xn-1),类似定理1 可得xn→q,且q=PFix(T)f(q).

设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.不妨定义:

任意x ∈H 和rn⊂(0,∞),其中T∶C→C 是连续伪压缩映射,A∶C→H 是连续单调映射.由上一章的引理可知Frn和Trn都是非扩张的且是单值的.

定理3　设C 是一致光滑严格凸的实Hilbert 空间H 的非空有界闭凸子集.设T∶C→C 是连续伪压缩映射A∶C→H 是连续单调映射.令S={S(s)∶0≤s < ∞}是C 上的非扩张半群使得以及=0.如果实数序列{αn},{βn},{γn},为[0,a),a ∈[0,1)中的实数序列,rn⊂(0,∞),>0 且满足F=F(S)∩F(T)∩VI(C,A)≠∅,映射Trn和Frn由上定义.序列{xn}由如下混合算法产生

则序列{xn}强收敛于z0=PFx0.

不动点及零点的迭代逼近及应用

相关推荐