Banach空间伪压缩映象的不动点定理

E 为一实Banach 空间,E∗为E 的对偶空间,〈·,·〉表示广义对偶对,称J∶E→2E∗为正规对偶映象,如果

Jx={f ∗∈E∗∶〈x,f ∗〉=‖x‖2=‖f ∗‖2},∀x ∈E.

今后均用j 表示单值赋范对偶映射.

设E 为一实Banach 空间,E∗为E 的对偶空间,C 为E 的一个闭凸子集.若S={x ∈E,‖x‖=1}为E 的单位球面,对任意的x,y ∈S,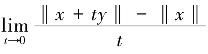一致存在,则称E 的范数是一致Gateaux 可微的.

若映射T∶C→C 满足条件

‖Tx-Ty‖≤‖x-y‖,∀x,y ∈C,

则称T 为非扩张的映射.

称映射A∶D(A)⊂E→E∗为单调的,对任意的x,y ∈D(A),如果下面的不等式成立:

〈x-y,Ax-Ay〉 ≥0.

其中D(A)表示算子A 的定义域,则称映射A∶D(A)⊂E→E∗为α 强单调的.若存在一个正实数α>0 使得对于任意的x,y ∈D(A),

〈x-y,Ax-Ay〉 ≥α‖Ax-Ay‖2.

显然,单调映射包含α 逆强单调映射.

设μ 是l∞上满足‖μ‖=1=μ(1)的连续线性泛函,则μ 是N 上的均值当且仅当

inf{an;n ∈N}≤μ(a)≤sup{an;n ∈N},∀a=(a1,a2,…)∈l∞.

如果以μn(an)代替μ(a),并且满足μn(an)=μn(an＋1),则称均值μn为Banach 极限.

定义映射φ(y)=μn‖xn-y‖2,∀y ∈E,则φ(y)是连续凸的且φ(y)→∞(‖y‖→∞).若E 是自反的,则存在z ∈C 使得φ(z)=因此

显然,Cmin是E 的闭凸子集.

引理1　设E 是具有一致Gateaux 可微范数的实Banach 空间,C 是E 的非空闭凸子集.设{xn}是E 中的有界序列,μn是Banach 极限且z ∈C,则

等价于

μn〈y-z,J(xn-z)〉≤0,∀y ∈C.

引理2　设α 是一实数,(x0,x1,…)∈l∞ 且对Banach 极限满足μn(xn)≤α.若 则.

引理3　设{an}为一非负实数序列且满足以下条件:

an＋1≤(1-θn)an＋σn,n ≥0,

其中{θn}是(0,1)中的序列且{σn}是实数列,使得

则=0.

Takahashi 为了研究有限簇非扩张的强收敛定理及其应用问题,引入了Wn映射的定义:

其中{Ti,i=1,2,…,N}是非扩张映射,由Takahashi 可知,Wn是非扩张的并且.

引理4　设{an}均为非负实数列,对任意λn∈[0,1],若存在正整数N 使得

an＋1≤(1-θn)an＋σn,∀n ≥N.

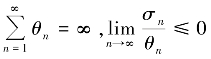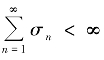其中或,则.

引理5　设{xn}和{zn}是Banach 空间中的有界序列,{βn}是[0,1]中的序列且满足如下条件:

假设

xn＋1=βnxn＋(1-βn)zn,n ≥0,

和

则=0.

引理6　设E 为一实Banach 空间,E∗为E 的对偶空间,J∶E→2E∗为正规对偶映像,则对任意的x,y ∈E,有

‖x＋y‖2≤‖x‖2＋2〈y,j(x＋y)〉,∀j(x＋y)∈J(x＋y).

Zegeye 介绍了如下的映射:

任意的x ∈H 和rn⊂(0,∞),其中T∶C→C 是一个连续伪压缩映射,A∶C→H 是一个连续单调映射.

引理7　Zegeye 设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令T∶C→C,是一严格连续伪压缩映射.Tr由上式定义,则如下结论成立:

(ⅰ)Tr是单值的;

(ⅱ)Tr是严格非扩张映射,即

〈Trx-Try,JTrx-JTry〉≤〈Trx-Try,Jx-Jy〉;

(ⅲ)F(Tr)=F(T);

(ⅳ)F(T)是闭凸的.

引理8　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.映射∏C∶E→C 是正则投影.假设x ∈E,则x0=∏Cx 等价于

〈z-x0,Jx-Jx0〉≤0,∀z ∈C.

我们可以类似定义一簇伪压缩算子对应的映射:

对任意的x ∈E 和rn⊂(0,∞),其中Ti∶C→C 是一簇连续伪压缩映射.

其中{Tirn,i=1,2,…,N}由上定义,且是非扩张映射.由Takahashi 可知,Wn是非扩张的,并且.

引理9　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一族严格非扩张映射使得≠∅.假设α=inf{αi}>0,则存在非扩张映射Γ∶C→C 使得.

证明　设αi,i=1,2,…,N 是[0,1]内的一组实数,且满足令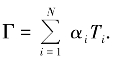 由于Ti是非扩张的,所以由文献[20]可知,Γ 是有意义的,且

这表明Γ 是非扩张的.下面将说明.首先,从Γ 是非扩张的推导中可知 ⊂F(Γ).现在将说明F(Γ)⊂ 令x ∈F(Γ),p ∈,则有

注意到Ti是非扩张的且αi,i=1,2,…,N 是[0,1]内的一组实数,这意味着〈Tix -x,j(x -p)〉=0,即Tix=x,i=1,2,…,N.从而,因此这就说明.

称序列{xn}满足条件(C):设E 是一个实Banach 空间,Tn∶C→C 是一簇非扩张映射,若序列{xn}弱收敛于x 且xn-Tnxn→0,则x ∈F,其中F=∩n≥1F(Tn).

假设C ⊆E 是有界闭凸子集,称映射Q∶E→C 为阳光的,若Q(tx＋(1-t)Q(x))=Q(x); 称映射Q∶E→E 是压缩的映射,当且仅当Q2=Q.若Q 是压缩的,则Q(z)=z,∀z ∈R(Q),其中R(Q)是Q 的值域.

引理10　设C 是光滑Banach 空间E 的非空子集.Q∶E→C 是一个压缩映射.J 是常规对偶映射,则如下几条等价:

(ⅰ)Q 是阳光非扩张的;

(ⅱ)〈x-Q(x),J(y-Q(x))〉≤0,∀x ∈E,y ∈C.

定理1　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射.对每个有界的序列xn和每个Banach 极限,假设Cmin由上定义且满足 ∩Cmin≠∅.设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和Wn由上定义.若序列xn由下式产生

其中{αn},{βn},{γn},{εn}为(0,1)中的实数例,且满足

则{xn}有界,且强收敛于Ti∶C→C,i=1,2,…,N 的公共不动点.

证明　由于{Ti,i=1,2,…,N}是伪压缩映射,由Takahashi 可知,Wn是非扩张的并且.设p ∈F,由Wn的非扩张性,可知

‖yn-p‖=‖εnxn＋(1-εn)Wnxn-p‖≤‖xn-p‖.

对于∀n ≥0,由f 的压缩性,可知

记,则‖xn-p‖≤M0,所以{xn}有界,进一步可得{yn},{Wnxn},{Wnyn},{f(xn)}均有界.

下面将说明‖xn＋1-xn‖→0.令xn＋1=βnxn＋(1-βn)wn.则有

又因为yn=εnxn＋(1-εn)Wnxn,所以有

又因为Tirn和Un,m都是非扩张映射,从Wn的定义可得

其中.

令vn=Un,N-1xn,vn＋1=Un＋1,N-1xn,un=TNrnvn,un＋1=TNrn＋1vn＋1,由Tirn的定义,则有

在第一式中令y=un＋1,在第二式中令y=un,则有

将两式相加,可得

因此,有下式成立

为不失一般性,假设b 是一个实数,使得rn>b>0,∀n ∈N.因此有

其中‖Ti,rnUn,i-1xn‖＋‖Un,i-1xn‖}.由于vn=Un,N-1xn,vn＋1=Un＋1,N-1xn,故

重复刚才的几步,可得类似的结果

因此可得

由于

再由Tirn的定义重复之前的步骤,得

其中M2=max{M1,sup{‖T1rnxn‖＋‖xn‖}}.进一步可得

从而

由定理条件可知,

由引理5 得=0,因此有

‖xn＋1-xn‖=| 1-βn| ‖wn-xn‖→0.

最后将说明{xn}强收敛于∩Cmin.由Cmin的定义,可知,再由引理1 可得

μn〈f(p)-p,j(xn-p)〉≤0.

由于J 是弱一致连续的对偶映象,可得

从而序列{〈f(p)-p,j(xn-p)〉}满足引理2 的条件.因此必有

另一方面,由引理2．4 可知

若记M3=sup‖xn-p‖2,整理上式得

令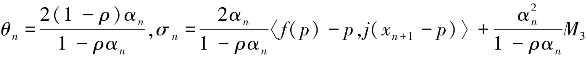,由于{xn}是有界的,由(13)和(14)以及条件(ⅰ)再根据引理3,可得=0,即序列{xn}强收敛于Ti∶C→C,i=1,2,…,N 的公共不动点p.

定理2　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射.对每个有界的序列xn和每个Banach 极限,假设Cmin由上定义且满足∅.设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和Wn由上定义.若序列xn由下式产生

其中{αn},{βn},{γn},{εn}为(0,1)中的实数列,且满足

则{xn}有界,且强收敛于Ti∶C→C,i=1,2,…,N 的公共不动点.

证明　由序列的定义可得

注意到序列{xn}和{Wnxn}的有界性,再根据定理条件,可得‖xn＋1-xn‖→0.类似于上面定理1,则可得该定理结论.

若在定理1 和定理2 中令f ≡u 为一常数函数,则可得如下推论.

推论1　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射.对每个有界的序列xn和每个Banach 极限,假设Cmin由上定义且满足∅.{Tirn,i=1,2,…,N}和Wn由上定义.若序列xn由下式产生

其中{αn},{βn},{γn},{εn}为(0,1)中的实数列,且满足

则{xn}有界,且强收敛于Ti,i=1,2,…,N 的公共不动点.

若在上面的定理中只考虑一个伪压缩映射,则可得下面的定理.

定理3　设C 是一致光滑严格凸的实Banach 空间E 的一个非空闭凸子集.令T∶C→C 是一个连续伪压缩映射.设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Trn由下式定义

对每个有界的序列xn和每个Banach 极限,假设Cmin由上定义且满足F=F(T)∩Cmin≠∅.{Tirn,i=1,2,…,N}和Wn由上定义.若序列xn由下式产生

其中{αn},{βn},{γn},{εn}为(0,1)中的实数列,且满足

则{xn}有界,且强收敛于T 的不动点.

证明　只需在Wn的定义中令αni=1,再由上面的定理1 和定理2 就可得该结论.

定理4　设C 是光滑严格凸的、自反的且具有一致Gateaux 可微范数的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射,Ai∶C→E∗,i=1,2,…,N 是一簇连续单调映射,使得 设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和{Firn,i=1,2,…,N}由上定义.若序列xn由下式产生:

其中{αn},{βn},{γn},{λn}为(0,1)中的实数列,且满足

则{xn}有界且强收敛于且是变分不等式≤0,∀y ∈F 的唯一解.

证明　首先说明{xn}是有界的.不妨取p ∈F,因为Firn是非扩张的,所以将得到

对于∀n ≥0,由于Firn,Tirn都是非扩张的且f 的压缩性,可知

所以{xn}有界,进一步可得{Tirnyn},{Firnxn},{yn},{f(xn)}均有界.

下面将说明‖xn＋1-xn‖→0.首先考虑

令vin=Firnxn,vin＋1=Firn＋1xn＋1,根据Firn的定义,我们可得

在第一式中令y=vin＋1,在第二式中令y=vin,则将得到

两式相加,则得到

由于AiA#,i=1,2,…,N 是单调映射,这表明

因此将得到

即

为不失一般性,假设b 是一个实数使得rn>b>0,∀n ∈N.因此有

其中,K=sup{‖vn＋1-xn＋1‖}.

从而有

另一方面,令un=Tirnyn,un＋1=Tirn＋1yn＋1,则可得

在第一式中令y∶=un＋1,在第二式中令y∶=un,可得

将上面两式相加,又因为Ti,{i=1,2,…,N}是伪压缩的,因此有

进一步可得

从而

其中,M=sup{‖un-yn‖}.

令xn＋1=βnxn＋(1-βn)zn,则有

由上面几个式子可得

注意到条件(ⅱ)和(ⅳ),将得到

再由引理4 可得

因此

‖xn＋1-xn‖=| 1-βn| ‖zn-xn‖→0.

从而

‖yn＋1-yn‖→0,‖un＋1-un‖→0,‖vn＋1-vn‖→0.

另外,由于xn＋1=αnf(xn)＋βnxn＋γnun,yn=λnxn＋(1-λn)vn,对∀p ∈F,由Ai的单调性和Tirn的非扩张性以及‖·‖2 的凸性可得(www.chuimin.cn)

因此有

因为αn→0,所以

‖xn-vn‖→0.

类似的,可以得到

‖xn-un‖→0.

从而

‖yn-xn‖=| 1-λn| ‖xn-vn‖→0,

‖yn-un‖≤‖yn-xn‖＋‖xn-un‖→0.

由于序列{xn}是有界的,因此存在{xn}的子序列{xnk}以及一个点w ∈C 使得xnk→w.又因为xn→vn,所以vnk→w.下面将说明w ∈F.

因为vn=Firnxn,根据映射Firn的定义,可得

令vt=tv＋(1-t)w,t ∈[0,1],∀v ∈C,可得

因为xnk-vnk→0,所以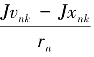→0,又因为Ai是单调的,所以有

从而

〈v-w,Aivt〉 ≥0.

若t→0,由Ai的连续性可得到〈v-w,Aiw〉 ≥0,即w ∈VI(C,Ai)和w ∈F2.

类似地,因为un=Tirnyn,由映射Tirn的定义,则有

令vt=tv＋(1 -t)w,t ∈[0,1],∀v ∈C.因为Ti是伪压缩的,所以有

因为ynk-unk→0,所以Junk-Jynk→0,故

从而有

〈w-vt,Tivt〉 ≥〈w-vt,Jvt〉.

〈v-w,Tivt〉≤〈v-w,Jvt〉.

若t→0,由Ti的连续性,可得〈v-w,Tiw-Jw〉 ≥0,∀v ∈C,这表明w=Tiw,即w ∈F(Ti),因此w ∈F1.从而w ∈F=F1∩F2.

因为 由引理8 可得

下面将说明由于un=Tirnyn,所以有

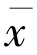其中,＋ 2ραn‖xn＋1-xn‖M1＋令θn=2αn(1 -ρ),则有=0,即序列{xn}强收敛于 ∈F.

由于

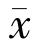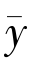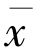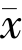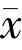这表明是变分不等式的解.下面将说明是该变分不等式的唯一解.假设 ∈F 是变分不等式的另一解.因为也是解,从而有(f -I),j(y-)〉≤0,∀y ∈F.又因为 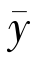∈F,所以有

另一方面,对于解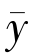 ∈F 来说,由于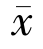∈F,所以

将上面两式相加,则有

因此

因为ρ ∈(0,1),所以可以得到,解的唯一性获证.

定理5　设C 是光滑严格凸的、自反的且具有一致Gateaux 可微范数的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射,Ai∶C→E∗,i=1,2,…,N 是一簇连续单调映射使得设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和{Firn,i=1,2,…,N}由上定义.若序列xn由下式产生:

其中{αn},{βn},{γn},为(0,1)中的实数列,且满足

则{xn}有界,且强收敛于且是变分不等式

的唯一解.在定理3 中取λn=0,则可得该结论.

如果在定理3 和定理4 中设f∶≡u ∈C 为一常数函数,则可得下面的推论.

推论2　设C 是光滑严格凸的、自反的且具有一致Gateaux 可微范数的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射,Ai∶C→E∗,i=1,2,…,N 是一簇连续单调映射使得 设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和{Firn,i=1,2,…,N}由上定义.若序列xn由下式产生x0∈C

其中,λn∈[0,1] 和{αn},{βn},{γn}是[0,1] 中的非负实数序列且满足

则序列xn强收敛于且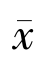是如下变分不等式的唯一解:

推论3　设C 是光滑严格凸的、自反的且具有一致Gateaux 可微范数的实Banach 空间E 的一个非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一簇连续伪压缩映射,Ai∶C→E∗,i=1,2,…,N 是一簇连续单调映射,使得设f 是一个具有压缩因子ρ ∈(0,1)的压缩映射.{Tirn,i=1,2,…,N}和{Firn,i=1,2,…,N}由上定义.若序列xn由下式产生:x0∈C

其中{αn},{βn},{γn}是[0,1] 中的非负实数序列,且满足

则序列xn强收敛于且是如下变分不等式的唯一解:

定理6　设C 是光滑严格凸的、自反的且具有一致Gateaux 可微范数的实Banach 空间E 的一个非空闭凸子集.令T∶C→C 是一个连续的伪压缩映射,A∶C→E 是一个连续的单调映射使得F=F(T)∩VI(C,A)≠∅,f∶C→C 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Trn和Frn由下式定义:x ∈E,rn∈(0,∞)

令序列xn由x0∈C 迭代生成

其中λn∈[0,1] 和{αn},{βn},{γn}是[0,1] 中的实数序列,且满足

则序列xn强收敛于且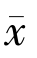是如下变分不等式的唯一解:

定理7　设E 是具有对偶E∗的光滑的、严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,m}是一簇连续伪压缩映射使得F ∩Cmin≠∅,f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射,Tirn和Wn如上所定义.设{xn}是由x0∈C 迭代生成的序列

其中{εn},{λn},{αn},{βn},{γn}是[0,1] 中的非负实数列且

则序列{xn}强收敛于Ti∶C→C,i=1,2,…,m 的公共不动点.

证明　首先说明{xn}是有界的.取p ∈F ∩Cmin,因为Wn是非扩张的,则有

对n ≥0,因为f 是压缩的,从(5)可得

因此,{xn}是有界的.进而可得{Wnxn},{Wnzn}和{yn},{f(xn)},{zn}都是有界的.

下面将说明

令xn＋1=βnxn＋(1-βn)wn,则有

因为yn=λnxn＋(1-λn)Wnzn,所以有

因此可得

又因为Tirn和Un,m都是非扩张映射,从Wn的定义可得

其中M=max{‖xn‖,‖Tm-i,rnUn,m-(i＋1)xn‖}.

令un=Tmrnvn,un＋1=Tmrn＋1vn＋1,vn=Un,m-1xn,vn＋1=Un＋1,m-1xn,由映射Tirn的定义可知

在上面两式中分别令y∶=un＋1和y∶=un,则有

将这两式相加,注意到Tm是伪压缩的,因此有

进而可得

为不失一般性,设存在某个常数b 使得rn>b>0,∀n ∈N,因此有

其中{‖Ti,rnUn,i-1xn‖＋‖Un,i-1xn‖}.

由于vn=Un,m-1xn,vn＋1=Un＋1,m-1xn,因此有

由Tirn的定义,重复以上步骤,可得

因此可得

从而可得

由Tirn的定义,可得

其中,M2=max{M1,sup{‖T1rnxn‖＋‖xn‖}},进而可得

同理可得

其中,‖Un,i-1zn‖},L2=max{L1,sup{‖T1rnzn‖＋‖zn‖}}.

从而由条件(ⅰ),(ⅱ)和(ⅲ),得

由引理5 得因此有‖xn＋1-xn‖=| 1 -βn|‖wn-xn‖→0.

最后将说明{xn}强收敛于p ∈F ∩Cmin.因为μn‖xn-p‖2= 由引理1 可得

由于J 是弱一致连续的对偶映象,从(23)可得

从而序列{〈f(p)-p,J(xn-p)〉}满足引理2．2 的条件.因此必有

另一方面,由于f 是具有压缩系数ρ ∈(0,1)的压缩映射,从引理6 可得

即

令 〈f(p)-p,J(xn＋1-p)〉＋由于{xn}是有界的,根据引理3,可得0,即序列{xn}强收敛于Ti∶C→C,i=1,2,…,m 的公共不动点.

定理8　设E 是具有对偶E∗的光滑的、严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令Ti∶C→C,i=1,2,…,m 是一族连续伪压缩映射使得F ∩Cmin≠∅.f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射,Tirn和Wn如上所定义.设{xn}是由x0∈C 迭代生成的序列

其中{εn},{λn},{αn},{βn},{γn}是[0,1] 中的非负实数列且

则序列{xn}强收敛于Ti∶C→C,i=1,2,…,m 的公共不动点.

证明　取p ∈F ∩Cmin,由式子(26)可得

注意序列{xn}和{Wnxn}的有界性,根据本定理条件(ⅰ)和(ⅱ),可得=0.再类似于定理7 的证明即可得到该定理的结果.

若在定理9 和定理10 中令f∶≡u ∈C 为一常数映射,则可得下面的推论.

推论4　设E 是具有对偶E∗的光滑的、严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令Ti∶C→C,i=1,2,…,m 是一族连续伪压缩映射使得F ∩Cmin≠∅,Tirn和Wn如(1)和(2)所定义.设xn是由x0∈C 迭代生成的序列

其中{εn},{λn},{αn},{βn},{γn}是[0,1] 中的非负实数列且

则序列{xn}强收敛于Ti∶C→C,i=1,2,…,m 的公共不动点.

定理9　设E 是具有对偶E∗的光滑的、严格凸的具有一致Gateaux 可微范数的自反实Banach 空间,C 是E 的非空闭凸子集.令T∶C→C 是连续伪压缩映射使得F(T)∩Cmin≠∅,f∶C→C 是具有压缩系数ρ ∈(0,1)的压缩映射.Trn由下式定义:x ∈C,rn∈(0,∞)

设序列{xn}由x0∈C 生成

其中{εn},{λn},{αn},{βn},{γn}是[0,1] 中的非负实数列且

则序列{xn}强收敛于T 的不动点.

定理10　设C 是Banach 空间E 的闭凸子集.令T∶C→C 是连续伪压缩映射,A∶C→H 是连续增生算子使得F(T)∩VI(C,A)≠∅.设Q∶C→F 是阳光非扩张的,f∶C→C 是具有压缩因子ρ ∈(0,1)的压缩映射.序列xn由x1∈C 生成

xn＋1=αnf(xn)＋βnxn＋γnTτnFτnxn

其中序列xn满足条件(C),{αn},{βn},{γn}是[0,1] 中的非负实数且

则序列xn收敛于且是如下变分不等式的唯一解:

证明　首先说明{xn}是有界的.不妨取p ∈F,则

对于∀n ≥0,因为Tτn和Fτn是非扩张的且f 是压缩的,所以有

因此,{xn}是有界的,从而可知{Fτnxn},{TτnFτnxn}和{f(xn)}都是有界的.

下面将说明‖xn＋1-xn‖→0.

令Un=TτnWn,Wn=Fτnxn,则有

其中K=sup{‖f(xn)‖＋‖Un‖∶n ∈N},L=‖xn‖＋‖Un‖∶n ∈N}.下面设‖Wn-Wn-1‖→0.

由于Wn=Fτnxn,Wn＋1=Fτn＋1xn＋1,根据Fτn的定义,有

在这两式中分别令y∶=Wn＋1和y∶=Wn,可得

将上面两式相加,有

由于A 是单调映射,这意味着

因此有

即

为了不失一般性,令b 是一个实数使得τn>b>0,∀n ∈N,则有

因此

由系数{αn},{βn},{τn}的限制条件可得

因此有

另一方面,因为Un=TτnWn,Un＋1=Tτn＋1Wn＋1,所以有

在这两式中分别令y∶=Un＋1和y∶=Un,则有

将两式相加,又因为T 是伪压缩的,所以有

因此

故

其中M1=sup{‖Un-Wn‖∶n ∈N}.再由{τn}的条件可得

又因为xn=αn-1f(xn-1)＋βn-1xn-1＋γn-1Tτn-1Fτn-1xn-1,因此

再由系数{αn},{βn}的条件可知

因为序列{xn}是有界的,所以存在{xn}的子序列{xnk}和w ∈C 使得xnk→w,又因为{xn}满足条件(C),因此w ∈F.

因为Q 是阳光非扩张的,且f 是压缩映射,所以Q(f)是压缩的.根据Banach 压缩定理,Q(f)具有唯一的不动点,且Q(f)的不动点正是f 的不动点.令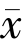 是f 的不动点,则有,因为J(x)是若连续的,所以

下面将说明xn→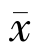∈F.

由于

令M2=sup‖xn-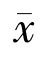‖2,所以

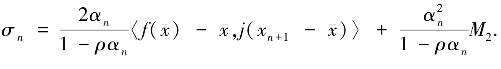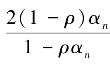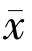其中若令λn=,则=0,即序列{xn}强收敛于∈F.

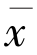根据Q 的性质可得 是上面变分不等式的解.现在将说明 是该变分不等式的唯一解.

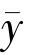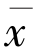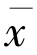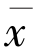假设∈F 是变分不等式的另一个解.因为 也是变分不等式的解,所以有〈f()-,j(y-)〉≤0,∀y ∈F.又因为 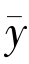∈F,所以有

另一方面,对于解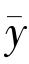 ∈F,因为 ∈F,所以

将两式相加,得

即

因此

因为ρ ∈(0,1)所以推出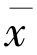=,解的唯一性得证.

定理11　设C 是Banach 空间E 的闭凸子集.令T∶C→C 是连续伪压缩映射,A∶C→H 是连续增生算子使得F(T)∩VI(C,A)≠∅.设Q∶C→F 是阳光非扩张的,f ≡u ∈C 为常数函数.序列xn由x1∈C 生成

其中序列xn满足条件(C),{αn},{βn},{γn}是[0,1] 中的非负实数且

则序列xn收敛于=Q(f(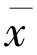))∈F 且 是如下变分不等式的唯一解: