Hilbert空间伪压缩映象的不动点定理

设C 是具有内积〈·,·〉 和范数‖·‖的实Hilbert 空间H 的闭凸子集.我们称映射A∶C→H 是单调的,当且仅当

〈x-y,Ax-Ay〉 ≥0,∀x,y ∈C.

称映射A∶C→H 为α 逆强单调的,若存在一个正实数α>0,使得

〈x-y,Ax-Ay〉 ≥α‖Ax-Ay‖2,∀x,y ∈C.

显然,单调映射包含α 逆强单调映射.单调映射是非线性映射中非常重要的一类映射.经典的变分不等式通常是指寻找一个点u ∈C 使得〈v-u,Au〉 ≥0,∀v ∈C.该变分不等式问题的解集通常记做VI(C,A).

称映射T 是伪压缩的,若∀x,y ∈C,

〈 Tx-Ty,x-y〉≤‖x-y‖2,∀x,y ∈C.

注意该不等式也可以等价写作

〈x-y-(Tx-Ty),x-y〉≤‖x-y‖2＋‖(I-T)x-(I-T)y‖2,∀x,y ∈C.

称映射T 是κ 严格伪压缩的,若存在常数0≤κ≤1 使得

〈x-y-(Tx-Ty),x-y〉≤‖x-y‖2-κ‖(I-T)x-(I-T)y‖2,∀x,y∈C.

若映射T∶C→C 满足条件

‖Tx-Ty‖≤‖x-y‖,∀x,y ∈C.

则称T 为非扩张的映射.显然,伪压缩映射包括严格伪压缩映射和非扩张映射.本书将以F(T)表示算子T 的不动点集,即F(T)={x ∈C∶Tx=x}.

称映射f∶C→C 为具有压缩因子的压缩映射,是指存在一个常数ρ ∈(0,1)使得

‖f(x)-f(y)‖≤ρ‖x-y‖,∀x,y ∈C.

引理1　设{an}为一非负实数序列且满足以下条件:

an＋1≤(1-θn)an＋σn,n ≥0,

其中{θn}是(0,1)中的序列且{σn}是实数列,使得

则an=0.

设C 是实Hilbert 空间H 的闭凸子集,称映射PC∶H→C 为测度投影.若对∀x ∈H,存在C 中的唯一点,记做PCx,使得

‖x-PCx‖≤‖x-y‖,∀y ∈C.

众所周知,PC是非扩张映射.

引理2　设C 是实Hilbert 空间H 的闭凸子集.令x ∈H,则PCx 具有如下的性质:

〈x-PCx,y-PCx〉≤0,∀x ∈H,y ∈C.

‖x-y‖2 ≥‖x-PCx‖2＋‖y-PCx‖2,∀x ∈H,y ∈C.

引理3　设C 是实Hilbert 空间H 的闭凸子集.令A∶C→H 是一个连续单调映射,T∶C→C 是一个连续伪压缩映射,定义映射Tr和Fr为如下形式:x ∈H,r ∈(0,∞)

则下面结论成立:

(ⅰ)Tr和Fr是单值的;

(ⅱ)Tr和Fr是严格非扩张映射,即

‖Trx-Try‖2≤〈Trx-Try,x-y〉,‖Frx-Fry‖2≤〈Frx-Fry,x-y〉;

(ⅲ)F(Tr)=F(T),F(Fr)=VI(C,A);

(ⅳ)F(T)和VI(C,A)是闭凸的.

引理4　设序列{xn}和{zn}是Hilbert空间中的有界序列,{βn}是[0,1]的序列且满足如下条件:

假设

xn＋1=βnxn＋(1-βn)zn,n ≥0,

和

则=0.

定理1　设K 为Hilbert 空间H 的非空闭凸子集,T∶K→K 为连续伪压缩映象且F(T)≠ϕ.设f∶K→K 是系数为ρ ∈(0,1)的压缩映象.对给定x0∈H,αn∈(0,1),rn∈(0,∞),如下定义{xn}:

其中A 是系数为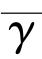的强正有界线性算子且 并满足下列条件:

则迭代序列{xn}强收敛到T 的某个不动点q,且满足〈(A -γf)q,q-w〉≤0,∀w ∈F(T).

证明　首先,证明序列{xn}有界.取p ∈F(T),记

由文献[11]引理2．6 可知p ∈F(Trn).由式(1)和文献[8]引理2．5 得

类似地,递推可得

因此{xn}有界,进一步可得{un},{Aun}和{f(xn)}有界.

其次,证明由序列定义得

其中,M1=sup{γ‖f(xn)‖＋‖Aun‖}.另一方面,由un=Trnxn∈K 和

由条件(ⅱ),不妨设rn≥k>0,得

其中M2=sup{‖un＋1-xn＋1‖}.由引理2 得

又因为‖xn-un‖≤‖xn-xn＋1‖＋αn‖γf(xn)-Aun‖,由条件(ⅰ)得

另一方面,由于{xn}有界,故存在一个弱收敛的子列{xni},不妨设xni⇀w.类似地,如果{uni}为{un}的一个弱收敛子列,则uni⇀w,且

记zt=tv＋(1-t)w,∀t ∈(0,1],v ∈K,得

且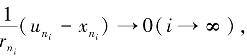 则

得

-〈Tzt,v-w〉 ≥-〈v-w,zt〉.

由T 的连续性可得

令v=Tw,得w=Tw,即w ∈F(T).

定义映象Φnx=tγf(x)＋(I-tA)Trnx,∀t ∈(0,1).对任意x,y ∈H,有

由于则Φn是压缩映象,故存在唯一的不动点.不妨设

xt=tγf(xt)＋(I-tA)Trnxt.

由于{xt}有界,所以

对给定w ∈F(T)=F(Trn),得

整理得

因为t ∈(0,1)且{xt}有界,故存在一个弱收敛子列xtj⇀q(tj→0).可知xtj→q,并且得q ∈F(T)=F(Trn).另一方面,

又因为Trn的非扩张性,不难验证

〈(I-Trn)x-(I-Trn)y,x-y〉 ≥0,∀x,y ∈H.

结合这两式得

将xt替换为xtj,由于(I-Trn)xtj→(I-Trn)q,则

因此

最后,证明{xn}强收敛到q ∈F(T)=F(Trn).

整理得

得=0.

定理2　设K 为Hilbert 空间H 的非空闭凸子集,T∶K→K 为连续严格伪压缩映象且F(T)≠ϕ.设f∶K→K 是系数为ρ ∈(0,1)的压缩映象,A 是系数为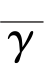的强正有界线性算子,且 对给定x0∈H,r ≥k>0,αn∈(0,1),如下定义{xn}:

且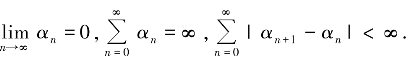则序列{xn}强收敛到T 的某个不动点q,且

〈(A-γf)q,q-w〉≤0,∀w ∈F(T).

引理5　设C 是实Hilbert 空间H 的一个有界非空闭凸子集.令Ti∶C→C,i=1,2,…,N 是一族严格非扩张映射使得 假设α=inf{αi}>0,则存在非扩张映射Γ∶C→C 使得.

证明　设αi,i=1,2,…,N 是[0,1] 内的一组实数,且满足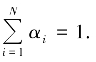令由于Ti是非扩张的,所以由文献[20] 可知,Γ 是有意义的且

注意到Ti是非扩张的且αi,i=1,2,…,N 是[0,1]内的一组实数,这意味着〈Tix -x,j(x -p)〉=0,即Tix=x,i=1,2,…,N.从而,因此这就说明了.

设C 是实Hilbert 空间H 的闭凸子集.令{Ai∶C→H,i=1,2,…,N}是一族连续单调映射,{Ti∶C→C,i=1,2,…,N}是一族连续伪压缩映射.Tirn∶E→C 和Firn∶E→C 是如下形式定义的映射:对x ∈E,rn∈(0,∞),

通过上面的引理可知Tirn和Firn都是有意义的,且它们都是非扩张的,F(Tirn)=F(Ti),F(Firn)=VI(C,Ai)是闭凸的.记,.

定理3　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一有限族连续的伪压缩映射,{Ai∶C→H,i=1,2,…,N}是一有限族连续单调映射使得F=F1∩F2≠∅,f∶C→C 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Tirn和Firn如上定义.令{xn}是由x0∈C 产生的序列

其中{αn},{βn},{γn},{εn}是[0,1] 中非负实数序列,μi≥0,σi≥0,i=1,2,…,N 和序列{un}⊂H 是一个很小的扰动使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

〈(f-I)w,y-w〉≤0,∀y ∈F.

证明　根据引理3 和引理5 可知,映射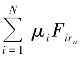和是有意义的.我们先证明{xn}是有界的.不妨取p ∈F,因为Firn,PC是非扩张的,所以有

对于n ≥0,因为Tirn和Firn是非扩张的且f 是压缩的,所以有

这表明

注意到条件(ⅳ),因此{xn}是有界的.相应的,{Firnxn},{Tirnyn}和{yn},{f(xn)}都是有界的.

下面将说明‖xn＋1-xn‖→0.由序列{yn}的定义可知

令vi,n=Firnxn,vi,n＋1=Firn＋1xn＋1,再根据映射Firn的定义,可得

在第一式中取y∶=vi,n＋1,在第二式中取y∶=vi,n,则有

将两式相加得

由于{Ai,i=1,2,…,N}是单调映射,这表明

因此

即

为不失一般性,不妨取b 是一个实数使得rn>b>0,∀n ∈N,则

其中,K=sup{‖vi,n＋1-xn＋1‖,i=1,2,…,N}.从而

另外,令wi,n=Tirnyn,wi,n＋1=Tirn＋1yn＋1,则得到

在第一式中取y∶=wi,n＋1,在第二式中取y∶=wi,n,则有

将这两个式相加,又因为{Ti,i=1,2,…,N}是伪压缩的,因此

进而

因此有

其中M=sup{‖wi,n-yn‖,i=1,2,…,N}.

令xn＋1=βnxn＋(1-βn)zn,则

由以上几个式子可得

注意条件(ⅱ)和(ⅲ),(ⅳ),因此有

所以由引理4 得

因此

‖xn＋1-xn‖=| 1-βn| ‖zn-xn‖→0.

从而

‖yn＋1-yn‖→0,‖wi,n＋1-wi,n‖→0,‖vi,n＋1-vi,n‖→0.

另外,由于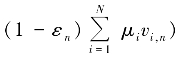,对∀p ∈F,由Ai的单调性和Tirn的非扩张性以及‖·‖2 的凸性,可得

因此有

由于αn→0,εn→0,故

‖xn-vi,n‖→0.

类似地,可得

‖xn-wi,n‖→0.

从而有

因为序列{xn}是有界的,故存在{xn}的子序列{xnk}和w ∈C 使得xnk若收敛到w.又因为xn→vi,n,因此vi,nk若收敛w.下面将说明w ∈F.

由于vi,n=Firnxn,根据映射Firn的定义,可得

令vt=tv＋(1-t)w,t ∈[0,1],∀v ∈C,有

因为{Ai,i=1,2,…,N}是单调的,又因为xnk-vi,nk→0,则有

从而有

〈v-w,Aivt〉 ≥0.

若t→0,根据Ai的连续性,则有〈v -w,Aiw〉 ≥0,即w ∈VI(C,Ai),因此w ∈F2.

类似地,因为wi,n=Tirnyn,根据映射Tirn的定义,有

令vt=tv＋(1 -t)w,t ∈[0,1],∀v ∈C.因为{Ti,i=1,2,…,N}是伪压缩映射,因此有

因为ynk-wi,nk→0,所以

从而

〈w-vt,Tivt〉 ≥〈w-vt,vt〉,

即

〈v-w,Tivt〉≤〈v-w,vt〉.(www.chuimin.cn)

若t→0,根据Ti的连续性,有〈v-w,Tiw-w〉≤0,∀v ∈C,可推出w=Tiw,即w ∈F(Ti),因此w ∈F1.从而w ∈F=F1∩F2.

记x∗=PFf(w),则 x∗ ∈ F 是满足如下式子的唯一点:infx∈F‖x -f(w)‖=‖x∗-f(w)‖.由引理1,可得〈f(w)-x∗,y -x∗〉≤0,∀y ∈ C.若取 y=f(w),则〈f(w)-x∗,f(w)-x∗〉≤0,故 f(w)=x∗.

利用空间H 上范数的弱下半连续性,有

这意味着

因此

在上面两式中分别取z∶=w 和z∶=x∗,则得

将这两式相加,可得〈x∗-w,x∗-w〉≤0,即‖w-x∗‖2≤0,因此w=x∗.再结合

可知序列xn→w=PFf(w)且w 是如下变分不等式的解

下面将说明w 是上面变分不等式的唯一解.

不妨假设∈F 是该变分不等式的另一个解,即

在

中令z∶=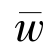,而在

中令z∶=w,则有

将两式相加,得

因此

因为ρ ∈(0,1)所以可推出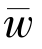=w,变分不等式的解的唯一性获证.

定理4　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一有限族连续的伪压缩映射,{Ai∶C→H,i=1,2,…,N}是一有限族连续单调映射,使得F=F1∩F2≠ϕ,f∶C→C 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Tirn和Firn如上定义.令{xn}是由x0∈C 产生的序列

其中{αn},{βn},{γn},{λn}A#{εn}是[0,1] 中非负实数序列,μi≥0,σi≥0,i=1,2,…,N 和序列{un}⊂H 是一个很小的扰动,使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

〈(f-I)w,y-w〉≤0,∀y ∈F.

证明　不妨取p ∈F,因为Firn,PC是非扩张的,因此有

对于n ≥0,因为Tirn和Firn是非扩张的且f 是压缩的,所以有

这表明

注意到条件(ⅳ),因此,{xn}是有界的,进而可知{Firnxn},{Tirnyn}和{yn},{f(xn)},PC(εnun＋(1-εn)都是有界的.

下面将说明‖xn＋1-xn‖→0.记则有

重复定理3 中的过程,则得到

因此

类似于定理1 的证明过程,可得该定理的结论.

若在定理3 和定理4 中取f∶≡u ∈C 为一个常数函数,则可得下面的推论.

推论1　设C 一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一有限族连续的伪压缩映射,{Ai∶C→H,i=1,2,…,N}是一有限族连续单调映射使得F=F1∩F2≠∅,u ∈C 是一个常数函数.Tirn和Firn如上定义.令{xn}是由x0∈C 产生的序列

其中{αn},{βn},{γn},{εn}是[0,1] 中的非负实数序列,μi≥0,σi≥0,i=1,2,…,N 以及序列{un}⊂H 是一个很小的扰动且满足下面的条件

则序列{xn}强收敛于w=PFu 且是下面变分不等式的唯一解:

推论2　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令{Ti∶C→C,i=1,2,…,N}是一有限族连续的伪压缩映射,{Ai∶C→H,i=1,2,…,N}是一有限族连续单调映射使得F=F1∩F2≠∅,u ∈C 是一个常数函数.Tirn和Firn如上定义.令{xn}是由x0∈C 产生的序列

其中{αn},{βn},{γn},{λn},{εn}是[0,1] 中非负实数序列,μi≥0,σi≥0,i=1,2,…,N 和序列{un}⊂H 是一个很小的扰动,使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

注记　若{un}⊂C,则定理1 和定理2 中的序列将变成reduces to

在相同的条件下,结论仍然成立.

若考虑单个伪压缩映射、单个单调映射,不妨定义映射Tr和Fr为如下形式:x ∈H,rn∈(0,∞)

定理5　设C 为一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令T∶C→C 是一连续的伪压缩映射,A∶C→H,是一连续单调映射使得F=F(T)∩VI(C,A)≠∅,f∶C→C 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Trn和Frn如上定义.令{xn}是由x0∈C 产生的序列

其中,{αn},{βn},{γn},{εn}是[0,1] 中非负实数序列,使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

〈(f-I)w,y-w〉≤0,∀y ∈F.

证明　先证明{xn}是有界的.不妨取p ∈F,因为Firn是非扩张的,所以有

对于n ≥0,因为Trn和Frn是非扩张的且f 是压缩的,所以有

这表明

因此{xn}是有界的.相应的{Frnxn},{Trnyn}和{yn},{f(xn)}都是有界的.

下面将说明‖xn＋1-xn‖→0.由序列{yn}的定义可知

令vn=Frnxn,vn＋1=Frn＋1xn＋1,再根据映射Frn的定义,可得

在上面两式中分别取y∶=vn＋1和y∶=vn,则有

将两式相加得

由于A 是单调映射,这表明

因此

即

为不失一般性,不妨取b 是一个实数使得rn>b>0,∀n ∈N,则

其中K=sup{‖vn＋1-xn＋1‖}.从而

另外,令wn=Trnyn,wn＋1=Trn＋1yn＋1,则得到

在上面两式中分别取y∶=wn＋1和y∶=wn,则有

将这两个式相加,又因为T 是伪压缩的,因此

进而

因此有

其中M=sup{‖wn-yn‖,i=1,2,…,N}.

令xn＋1=βnxn＋(1-βn)zn,则

由以上几个式子可得

注意条件(ⅱ)和(ⅲ),(ⅳ),因此有

所以由引理得

因此

‖xn＋1-xn‖=| 1-βn| ‖zn-xn‖→0.

从而

‖yn＋1-yn‖→0,‖wn＋1-wn‖→0,‖vn＋1-vn‖→0.

另外,由于xn＋1=αnf(xn)＋βnxn＋γnwn,yn=εnxn＋(1-εn)vn,对∀p ∈F,由A 的单调性和Trn的非扩张性以及‖·‖2 的凸性,可得

因此有

由于αn→0,εn→0,故

‖xn-vn‖→0.

类似地可得

‖xn-wn‖→0.

从而有

‖yn-xn‖≤| (1-εn)| ‖xn-vn‖→0,

‖yn-wn‖≤‖yn-xn‖＋‖xn-wn‖→0.

因为序列{xn}是有界的,故存在{xn}的子序列{xnk}和w ∈C 使得xnk若收敛于w.又因为xn→vn,因此vnk弱收敛于w.下面将说明w ∈F.

由于vn=Frnxn,根据映射Frn的定义,可得

令vt=tv＋(1-t)w,t ∈[0,1],∀v ∈C,有

因为A 是单调的,又因为xnk-vnk→0,所以

从而有

〈v-w,Avt〉 ≥0.

若t→0,根据Ai的连续性,则有〈v-w,Aw〉 ≥0,即w ∈VI(C,A).

类似地,因为wn=Trnyn,根据映射Trn的定义,有

令vt=tv＋(1 -t)w,t ∈[0,1],∀v ∈C.因为T 是伪压缩映射,因此有〈wnk-vt,Tvt〉 ≥〈wnk-vt,Tvt〉＋〈vt-wnk,Twnk〉 -

因为ynk-wnk→0,所以

从而

〈w-vt,Tvt〉 ≥〈w-vt,vt〉,

即

〈v-w,Tvt〉≤〈v-w,vt〉.

若t→0,根据Ti的连续性,有〈v -w,Tw-w〉≤0,∀v ∈C,可推出w=Tw,即w ∈F(T),从而w ∈F=F(T)∩VI(C,A).

记x∗=PFf(w),则x∗∈F 是满足如下式子的唯一点:f(w)‖=‖x∗-f(w)‖.由引理1,可得〈f(w)-x∗,y-x∗〉≤0,∀y ∈C.若取y=f(w),则〈f(w)-x∗,f(w)-x∗〉≤0,故f(w)=x∗.

利用空间H 上范数的弱下半连续性,有

这意味着

因此

〈z-x∗,x∗-f(w)〉 ≥0,∀z ∈C.

〈z-w,w-f(w)〉 ≥0,∀z ∈C.

在第一式总取z∶=w 在第二式中取z∶=x∗,则得

〈w-x∗,x∗-f(w)〉 ≥0,∀z ∈C.

〈x∗-w,w-f(w)〉 ≥0,∀z ∈C.

将这两式相加,可得〈x∗-w,x∗-w〉≤0,即‖w-x∗‖2≤0,因此w=x∗.再结合

可知序列xn→w=PFf(w)且w 是如下变分不等式的解:

〈z-w,(f-I)w〉≤0,∀z ∈C.

下面将说明w 是上面变分不等式的唯一解.

不妨假设∈F 是该变分不等式的另一个解,即

在

〈z-w,(f-I)w〉≤0,∀z ∈C

中令z∶=,而在

中令z∶=w,则有

将两式相加,得

因此

因为ρ ∈(0,1),所以可推出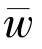=w,变分不等式的解的唯一性获证.

定理6　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令T∶C→C 是一连续的伪压缩映射,A∶C→H,是一连续单调映射使得F=F(T)∩VI(C,A)≠∅,f∶C→C 是一个具有压缩因子ρ ∈(0,1)的压缩映射.Trn和Frn如上定义.令{xn}是由x0∈C 产生的序列

xn＋1=αnf(xn)＋βnxn＋γnTrnFrnxn,

其中{αn},{βn},{γn}是[0,1] 中非负实数序列,使得

则序列{xn}强收敛于w=PFf(w),且w 是如下变分不等式的唯一解:

〈(f-I)w,y-w〉≤0,∀y ∈F.

证明　只需在定理3 中取εn=0,则可得到该结论.

若在定理7 和定理8 中取f∶≡u ∈C 为一个常数函数,则可得下面的定理.

定理7　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令T∶C→C 是一连续的伪压缩映射,A∶C→H 是一连续单调映射,使得F=F(T)∩VI(C,A)≠∅,u ∈C 是一个常数函数.Trn和Frn如上定义.令{xn}是由x0∈C 产生的序列

其中{αn},{βn},{γn},{εn}是[0,1] 中非负实数序列,使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

〈u-w,y-w〉≤0,∀y ∈F.

定理8　设C 是一致光滑严格凸的实Hilbert 空间H 的非空闭凸子集.令T∶C→C 是一连续的伪压缩映射,A∶C→H,是一连续单调映射,使得F=F(T)∩VI(C,A)≠∅,u ∈C 是一个常数函数.Trn和Frn如上定义.令{xn}是由x0∈C 产生的序列

xn＋1=αnu＋βnxn＋γnTrnFrnxn,

其中{αn},{βn},{γn}是[0,1] 中非负实数序列,使得

则序列{xn}强收敛于w=PFf(w)且w 是如下变分不等式的唯一解:

〈(u-w,y-w〉≤0,∀y ∈F.