非线性算子的性质及应用

2025-09-30 理论教育版权反馈

【摘要】：非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.设E1和E2时两个实Banach 空间,D E1.设A∶D→E2为非线性的.定义1设x0∈D.若ε>0,δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而

非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.

设E1和E2时两个实Banach 空间,D ⊆E1.设A∶D→E2为非线性的.

定义1　设x0∈D.若∀ε>0,∃δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而与x0∈D 无关,则称A 在D 上一致连续.

显然,A 在x0∈D 连续的充分必要条件是:对任何xn∈D,xn→x0,都有Axn→Ax0.

定义2　若A 将D 中的任何有界集变为E2中的有界集,则称A 在D 上有界.

众所周知,对于线性算子来讲,连续性与有界性是等价的.但是对于非线性算子,则没有这样的等价关系.

定义3　若A 将D 中任何有界集S 映成E2的列紧集A(S)(即A(S)是相对紧集,亦即它的闭包是E2中的紧集),则称A 是映D 入E2的紧算子.

显然,A 在D 上紧的充要条件是:对于D 中任何有界序列{xn},必有子序列{xnk}存在,使得序列{Axnk}在E2中收敛.另外,紧算子必有界.

定义4　若算子A∶D→D2连续,而且又是紧的,则称A 是映D 入E2的全连续算子.

定理1　设An∶D→E2全连续(n=1,2,…),A∶D→E2.如果对于D 中任何有界集S,当n→∞时,‖Anx -Ax‖都一致趋于零,那么A∶D→E2全连续.

关于全连续算子,介绍下面两个常用的一般性定理.

定理2　设A∶D→E2且D 是E1中有界集,则下列三个结论是等价的:

(ⅰ)A∶D→E2全连续;(https://www.chuimin.cn)

(ⅱ)∀ε>0,∃Aε∶D→Eε连续有界,使得对于一切x ∈D 均有‖Ax-Aεx‖ < ε,这里Eε是E2的某个有限维子空间;

(ⅲ)A 可以表示为 pagenumber_ebook=27,pagenumber_book=20 其中An∶D→En(0)连续有界,En(0)表示E 的某个有限维子空间,且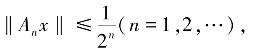∀x ∈D.

Frechet 微分和Frechet 算子的概念是应用上用得最多的微分和导算子的概念．下面介绍一下Frechet 微分．

定义5　设E1和E2是Banach 空间,D 是E1中某开集,A∶D→E2,x0∈D.若∃B(E1→E2),使得

A(x0＋h)-Ax0=Bh＋ω(x0,h),

其中ω(x0,h)=o(‖h‖),即

则称算子A 在点x0处Frechet 可微,Bh 叫作A 在x0处对于h 的Frechet 微分,记为d[A(x0)h];算子B 叫作A 在x0点的Frechet 导算子,记做A′(x0).

明显的,Frechet 微分概念对于算子的要求是较强的,在讨论算子的某些问题时,可将条件减弱,从而得到较弱的微分和导算子的概念,即Gateaux 微分和Gateaux 算子概念.这种微分和导算子的概念是方向导数概念的推广.

定义6　设A∶D→E2,D 是E1中的开集,x0∈D.若对任何h ∈E1,极限

都存在,则称算子A 在点x0处Gateaux 可微,极限叫作A 在x0处的Gateaux 微分,记为D[A(x0)h];若Gateaux 微分表示为D[A(x0)h]=Bh,则称算子B 叫作A 在x0点的Gateaux 导算子.

注意,若A 在x0处具有有界线性的Gateaux 微分,则一般不能推出A 在x0处Frechet 可微.

非线性算子的性质及应用

相关推荐