首页理论教育ANSYSWorkbench17.0热应力基本理论实例演练

ANSYSWorkbench17.0热应力基本理论实例演练

2023-10-20 理论教育版权反馈

【摘要】：为了进一步了解热应力的概念、产生原因、约束方式及求解原理，下面用材料力学的方法讨论几个简单的热应力例子。即棒1受压应力σ1的作用，相应的应变，缩短量；棒2受拉应力σ2的作用，相应的应变，缩短量。棒1的最终伸长量为棒2的最终伸长量为注意上两式中，ε1、σ1、ε2、σ2包含有符号，拉应力为正号，压应力为负号。

为了进一步了解热应力的概念、产生原因、约束方式及求解原理，下面用材料力学的方法讨论几个简单的热应力例子。

1.棒两端约束时的热应力问题

长度为l、直径为d的圆棒，两端固定在刚体壁处，不能沿长度自由度伸缩，如图11-1所示。

当棒由初始温度t₀冷却到t₁时，在自由状态下，棒的缩短量为∆l=α（t₀−t₁）l。

其中，∆l是无约束时棒与壁之间应出现的间隙。由于棒两端是固定的，因此刚体壁对棒产生拉伸作用，拉伸力为P，故棒内的拉伸应力为

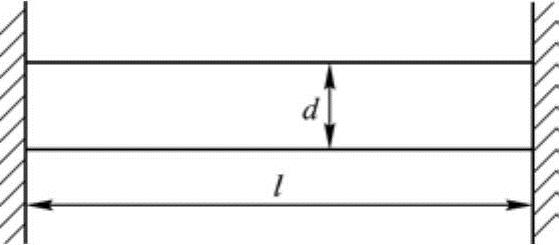
图11-1 预应力模型

另外，棒被拉伸后，其应变及相应的应力是

式（11-3）与式（11-5）应相等，由此解出

将式（11-6）代回式（11-3），得到棒的热应力值为

σ=εE（t₀−t₁）=αEt （11-7）

其中，t表示温度的变化。式（11-7）对于圆棒加热也是适用的，只是此时棒受压缩，σ为负值。

2.两根长度相同的棒互相约束

图11-2所示为两根长度都等于l但材料不同的棒连接在一起，不能相对移动，也不发生弯曲。两棒的初始温度都等于t₀，最终温度分别为t₁和t₂，且棒内的温度均匀分布。(www.chuimin.cn)

图11-2 两个棒相互约束

为了讨论方便，不妨假设t₁＞t₂及α₁＞α₂（下标1和2分别对应棒1和棒2）。

如果两棒之间是没有相互约束的，则棒1的自由膨胀量∆l₁=α₁（t₁−t₀）l，棒2的自由膨胀量∆l₂=α₂（t₂−t₀）l。

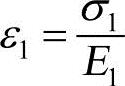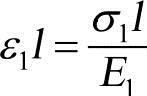故∆l₁＞∆l₂，但由于两棒固定在一起，长度方向不能相对移动，因此棒1的实际膨胀值小于自由膨胀值，而棒2的实际膨胀值大于自由膨胀值。即棒1受压应力σ₁的作用，相应的应变，缩短量；棒2受拉应力σ₂的作用，相应的应变，缩短量。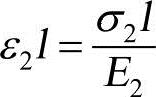

棒1的最终伸长量为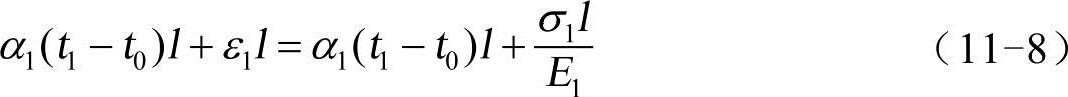

棒2的最终伸长量为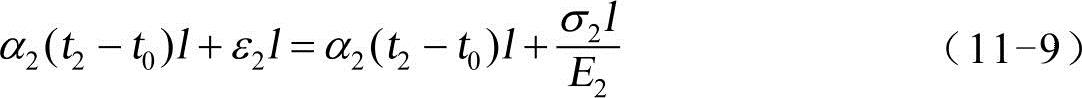

注意上两式中，ε₁、σ₁、ε₂、σ₂包含有符号，拉应力为正号，压应力为负号。由于两棒长度保持相等，故有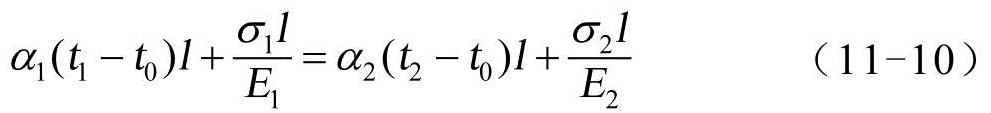

此时两棒处于平衡状态，因无其他外力作用，棒1所受的压缩力与棒2所受到的拉伸力相等，即

σ₁A₁=σ₂A₂ （11-11）

式中，A₁、A₂分别为棒1与棒2的横截面积。

由式（11-8）和式（11-9）联立解得

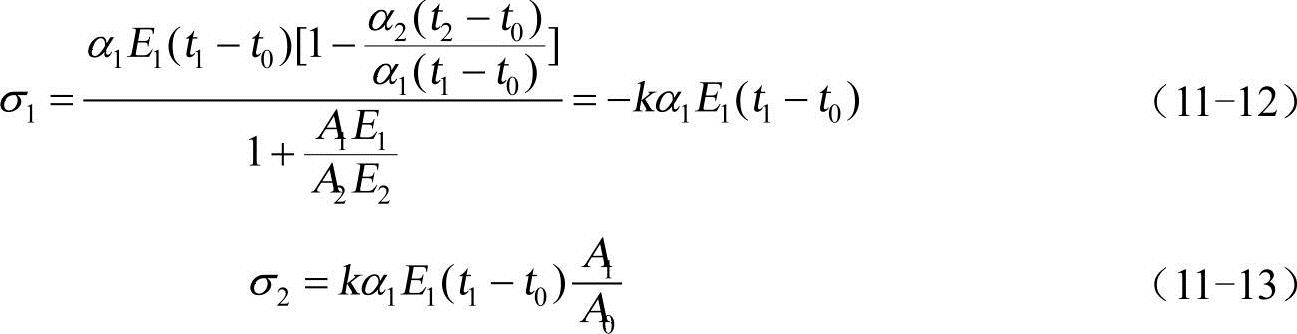
其中，k值为

k称为约束系数，若k＞0，则σ₁＜0、σ₂＞0，棒1为压应力，棒2为拉应力；若k＜0，则σ₁＞0、σ₂＜0。

以上讨论的是两棒长度相等的情形，如果两棒长度不相等，只要是相互约束的，就可按与上相同的原理求解。