【摘要】:基本概念①温度场温度场是指某一时刻空间各点温度的总称。傅里叶定律傅里叶在实验研究导热过程的基础上,把热流矢量和温度梯度联系起来,得到q=λgradt 上式就是1822年由傅里叶提出的导热基本定律的数学表达式,亦称为傅里叶定律。傅里叶定律确定了热流密度矢量和温度梯度的关系。
(1)基本概念
①温度场
温度场是指某一时刻空间各点温度的总称。一般地说,它是时间和空间的函数,对直角坐标系即:
t=f(x,y,z,τ) (1-9)
式中t——温度;
x,y,z——直角坐标系的空间坐标;
τ——时间。
式(1-9)表示物体的温度在x,y,z三个方向和在时间上都发生变化的三维非稳态温度场。如果温度场不随时间而变化,即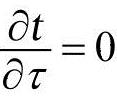 ,则为稳态温度场,这时,t=f(x,y,z,τ)。如果稳态温度场仅和两个或一个坐标有关,则称为二维或一维稳态温度场。一维稳态温度场可表示为:
,则为稳态温度场,这时,t=f(x,y,z,τ)。如果稳态温度场仅和两个或一个坐标有关,则称为二维或一维稳态温度场。一维稳态温度场可表示为:
t=f(x) (1-10)
它是温度场中最简单的一种情况,例如高宽远大于其厚度的大墙壁内的导热就可以认为是一维导热。具有稳态温度场的导热过程叫作稳态导热。温度场随时间变化的导热过程叫作非稳态导热。
②等温面与等温线
同一时刻,温度场中所有温度相同的点连接所构成的面叫作等温面。不同的等温面与同一平面相交,则在此平面上构成一簇曲线,称为等温线。在同一时刻任何给定地点的温度不可能具有一个以上的不同值,所以两个不同温度的等温面或两条不同温度的等温线绝不会彼此相交。它们或者是物体中完全封闭的曲面(线),或者就终止于物体的边界上。
在任何时刻,标绘出物体中的所有等温面(线),就给出了物体内的温度分布情形,亦即给出了物体的温度场。所以,习惯上物体的温度场用等温面图或者等温线图来表示。图1-3就是用等温线图表示温度场的示例。
③温度梯度
在等温面上,不存在温度差异,因此,沿着等温面不可能有热量的传递。热量传递只发生在不同的等温面之间。自等温面上的某点出发,沿着不同方向到达另一等温面时,将发现单位距离的温度变化,即温度的变化率,具有不同的数值。自等温面上某点到另一个等温面,以该点法线方向的温度变化率为最大。沿该点法线方向,数值也正好等于这个最大温度变化率的矢量称为温度梯度,用gradt表示,正向(符号取正)是朝着温度增加的方向,如图1-4所示。
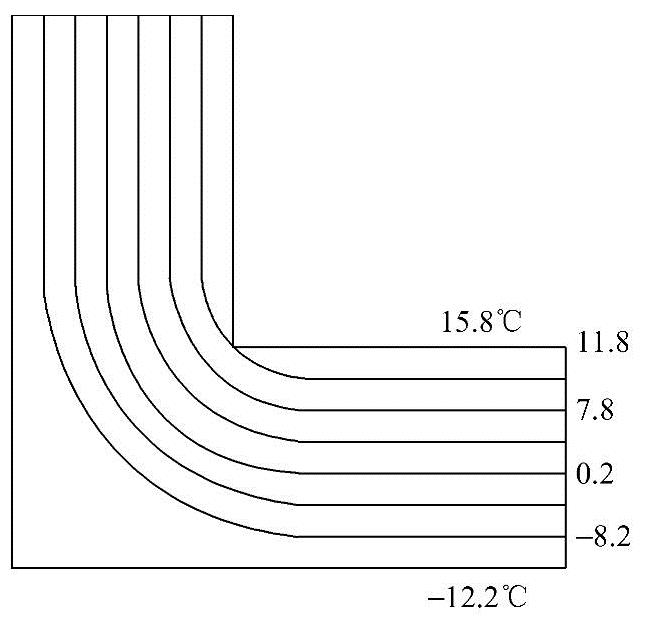
图1-3 房屋墙角内的温度场
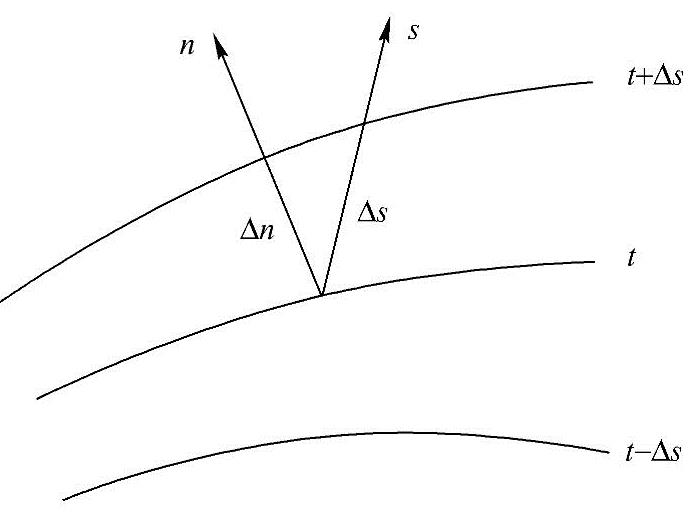
图1-4 温度梯度
 (www.chuimin.cn)
(www.chuimin.cn)
式中,n为法线方向上的单位矢量,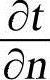 为沿着法线方向温度的方向导数。温度梯度在直角坐标系三个坐标轴上的分量分别为
为沿着法线方向温度的方向导数。温度梯度在直角坐标系三个坐标轴上的分量分别为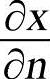 、
、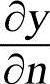 、
、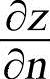 。而且
。而且

式中,i、j和k分别为三个坐标轴方向的单位矢量。温度梯度的负值,−gradt称为温度降度,它是与温度梯度数值相等而方向相反的矢量。
④热流密度矢量
单位时间单位面积上所传递的热量称为热流密度。在不同方向上,热流密度的大小是不同的。与定义温度梯度相类似,等温面上某点以通过该点最大热流密度的方向为方向,数值上也正好等于沿着该方向热流密度的矢量称为热流密度矢量。其他方向的热流密度都是热流矢量在该方向的分量。热流密度矢量q在直角坐标系三个坐标轴上的分量为qx、qy、qz。而且:
q=qxi+qyj+qzk (1-13)
式中,i、j、k分别为三个坐标方向的单位矢量。
(2)傅里叶定律
傅里叶在实验研究导热过程的基础上,把热流矢量和温度梯度联系起来,得到
q=−λgradt(W/m2) (1-14)
上式就是1822年由傅里叶提出的导热基本定律的数学表达式,亦称为傅里叶定律。式中的比例系数λ称为导热系数。
式(1-14)说明,热流密度矢量和温度梯度位于等温面的同一法线上,但指向温度降低的方向,如图1-5所示,式中的负号表示热流矢量的方向与温度梯度的方向相反,永远顺着温度降低的方向。
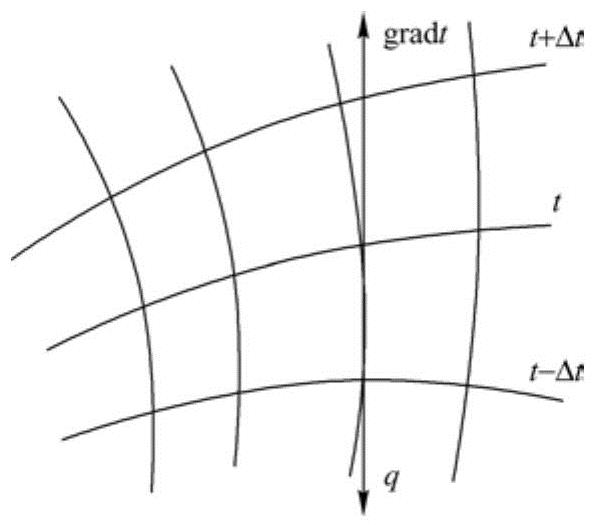
图1-5 热流密度矢量和温度梯度
按照傅里叶定律和式(1-12)和(1-13)可以看出,热流密度矢量x、y和z轴的分量应为

值得指出的是,式(1-14)和式(1-15)中隐含着一个条件,就是导热系数在各个不同方向是相同的。这种导热系数与方向无关的材料称为各向同性材料。
傅里叶定律确定了热流密度矢量和温度梯度的关系。因此要确定热流矢量大小,就必须知道温度梯度,亦即物体内的温度场。

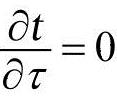 ,则为稳态温度场,这时,
,则为稳态温度场,这时,

 (www.chuimin.cn)
(www.chuimin.cn)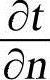 为沿着法线方向温度的方向
为沿着法线方向温度的方向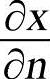 、
、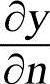 、
、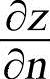 。而且
。而且








相关推荐