第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.注意到1～8的自然数列中处于“中心”对称位置上的两个自然数，其和都等于8+1=9，我们共有4对这样的自然数1，8；2，7；3，6和4，5，在每对自然数中随意选取一个自然数，将这4个自然数随意排序，余下的4个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于8+1=9.比如我们取7，3，4，8，1，5，6，2这样的顺序，相应的自......
2023-10-20
同基因8阶二次兼完美幻方的产生幻中之幻
【摘要】：任何一个8阶二次兼完美幻方都可以以下四组共16个（包括其本身）对称变换各得到一个同基因的8阶二次兼完美幻方：为方便起见，标志①～⑧依次表示已知的8阶二次兼完美幻方的第1行至第8行，以从左到右的顺序表示其在新幻方中的行数.四组对称变换如下，在以下每一个行变换后，列亦要做同样的对称变换.Ⅰ.⑴①②③④ ⑤⑥⑦⑧⑵④③②① ⑧⑦⑥⑤⑶①③②④ ⑤⑦⑥⑧⑷④②③① ⑧⑥⑦⑤Ⅱ.⑴②①④③ ⑥⑤⑧⑦⑵③④①
任何一个8阶二次兼完美幻方都可以以下四组共16个（包括其本身）对称变换各得到一个同基因的8阶二次兼完美幻方：
为方便起见，标志①～⑧依次表示已知的8阶二次兼完美幻方的第1行至第8行，以从左到右的顺序表示其在新幻方中的行数.四组对称变换如下，在以下每一个行变换后，列亦要做同样的对称变换.
Ⅰ.⑴①②③④ ⑤⑥⑦⑧
⑵④③②① ⑧⑦⑥⑤
⑶①③②④ ⑤⑦⑥⑧
⑷④②③① ⑧⑥⑦⑤
Ⅱ.⑴②①④③ ⑥⑤⑧⑦
⑵③④①② ⑦⑧⑤⑥
⑶②④①③ ⑥⑧⑤⑦
⑷③①④② ⑦⑤⑧⑥
Ⅲ.⑴①⑥⑦④ ⑤②③⑧
⑵⑤②③⑧ ①⑥⑦④
⑶④⑥⑦① ⑧②③⑤
⑷⑧②③⑤ ④⑥⑦①(www.chuimin.cn)
Ⅳ.⑴②⑤⑧③ ⑥①④⑦
⑵⑥①④⑦ ②⑤⑧③
⑶③⑤⑧② ⑦①④⑥
⑷⑦①④⑥ ③⑤⑧②
比如，对8阶二次兼完美幻方C1按对称变换Ⅰ.⑵，我们有与其同基因的8阶二次兼完美幻方C7，如图19-17所示.
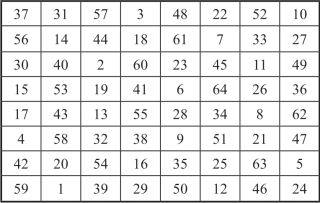
图19-17 同基因8阶二次兼完美幻方C7
按对称变换Ⅳ.⑵，我们有与C1同基因的8阶二次兼完美幻方C8，如图19-18所示.
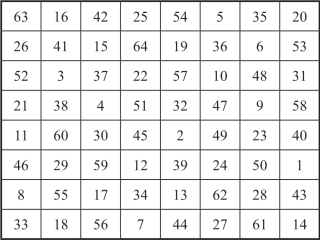
图19-18 同基因8阶二次兼完美幻方C8
8阶二次兼完美幻方C1，C7与C8相应行，列，对角线由相同元素成，所以它们是同基因的8阶二次兼完美幻方.
读者可按所列其他对称变换或读者自己发现的对称变换，由一个已知的8阶二次兼完美幻方去得到一个同基因的8阶二次兼完美幻方.
如果采取类似的方式去获取一个属于你自己的8阶二次兼完美幻方，在探索过程中只需检测方阵A与方阵B相同行，列及对角线同一位置上两个元素乘积之和是否等于126，即可预判所得结果是否一个8阶二次兼完美幻方，不必等到出了结果再去验算.
有关幻中之幻的文章
- 详细阅读
-
构造6个异基因8阶二次兼完美幻方-《幻中之幻详细阅读
⑴先构造头一对8阶二次兼完美幻方.第一步，由8组0～7的自然数构造一个非正规的8阶完美幻方，如图19-1方阵1A所示.图19-1方阵A1由8组1～8的自然数构造一个非正规的8阶完美幻方，如图19-2方阵B1所示.图19-2方阵B1但要保证方阵A1，方阵B1对应行，列，对角线上相同位置上元素乘积之和都为126.第二步，方阵A1的元素乘以8，再加上方阵B1相同位置上的数字，就得到方阵C1.方阵C1......
2023-10-20
- 详细阅读
-
4阶最完美幻方：幻中之幻详细阅读
第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2023-10-20
-
最完美的8阶最简单幻方—幻中之幻详细阅读
第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.第1列按自上而下的顺序安装自然数1～8，第2列按自下而上的顺序安装自然数9～16，第3列按自上而下的顺序安装自然数17～24，第4列按自下而上的顺序安装自然数25～32；第8列按自下而上的顺序安装自然数33～40，第7列按自上而下的顺序安装自然数41～48，第6列按自下而上的顺序安装自然数49～56，第5列按自上而下的顺序安装自然数57～6......
2023-10-20
-
构造5阶易位完美幻方：幻中之幻详细阅读
从1～9的自然数中任意选定5个数，比如1，3，6，5，8，它们的和是23.任意选定另外5个数，使它们的和亦是23，比如9，2，7，1，4.1，3，6，5，8，各取5次，仿照构造完美幻方的两步法[1]，得到一个不连续数的五阶完美幻方，其幻方常数为是23.其基方阵如图2-12所示，所得不连续数的5阶完美幻方，如图2-13所示.图2-125阶基方阵图2-13不连续数的5阶完美幻方9，2，7，1，4.......
2023-10-20
-
构造完美7阶幻方-幻中之幻详细阅读
第一步，由构造对称完美幻方的两步法[1]得到的一个7阶对称完美幻方，其幻方常数是175.中心对称位置上两个元素之和都等于50.其基方阵A如图5-9所示，7阶对称完美幻方如图5-10所示.图5-97阶基方阵A图5-107阶对称完美幻方上述7阶对称完美幻方其所有数都加10，得一个新的由11～59的自然数组成的非正规的7阶对称完美幻方B，如图5-11所示.图5-11非正规的7阶对称完美幻方B第二步......
2023-10-20
- 详细阅读
相关推荐