如何借助于两步法去构造奇数n=2m+1（m为m≠3t+1t＝0，1，2，…的自然数）阶完美或对称完美的砍尾巴幻方？......
2023-10-20
幻中之幻-9阶二次兼对称幻方
【摘要】：这里共得到了9个9阶二次幻方.还能得到更多的9阶二次幻方吗？
若要构造一个9阶二次幻方，首先要解决的一个问题是，1～81如何平均分成9组，且使每组9个数的和相等，其平方和亦相等.
第一步，寻找构成基方阵A的3个3×9方阵.
⑴构成基方阵A的第一个3×9方阵A1.
图18-1是1个3×3的方阵，每行3个数字之和都等于15.
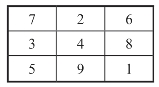
图18-1 3×3的方阵
图18-2是1个1×9的方阵，9个数字之和等于324.
图18-2 1×9的方阵
图18-3是1个由图18-1 3×3的方阵衍生的3×9方阵，每行9个数字之和都等于45.
图18-3 衍生的3×9方阵
图18-4是1个3×9方阵，由图18-3各列的3个数都加上图18-2同列的数所得.
图18-4 构成基方阵A的3×9方阵A1
图18-4每行9个数字之和都等于369，其平方和都等于20049.
⑵构成基方阵A的第二个3×9方阵A2.
图18-1 3×3方阵各行向右顺移一个位置得1个新的3×3的方阵，如图18-5所示.
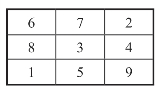
图18-5 右移所得3×3方阵
图18-6是1个由图18-5 3×3的方阵衍生的3×9方阵，每行9个数字之和都等于45.
图18-6 衍生的3×9方阵
图18-7是1个3×9方阵，由图18-6各列的3个数都加上图18-2同列的数所得.
图18-7 构成基方阵A的3×9方阵A2
图18-7每行9个数字之和都等于369，其平方和都等于20049.
⑶构成基方阵A的第三个3×9方阵A3.
图18-5 3×3方阵各行向右顺移一个位置又得1个新的3×3的方阵，如图18-8所示.
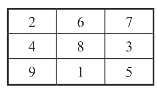
图18-8 再次右移所得3×3方阵
图18-9是1个由图18-8 3×3的方阵衍生的3×9方阵，每行9个数字之和都等于45.
图18-9 衍生的3×9方阵
图18-10是1个3×9方阵，由图18-9各列的3个数都加上图18-2同列的数所得.
图18-10 构成基方阵A的3×9方阵A3
图18-10每行9个数字之和都等于369，其平方和都等于20049.
第二步，构造基方阵A.
图18-4方阵A1，图18-7方阵A2和图18-10方阵A3从上到下依次排在一起组成1个9×9方阵，称为基方阵A，如图18-11所示.
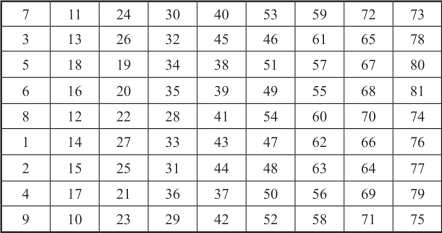
图18-11 基方阵A
基方阵A每行9个数字之和都等于369，其平方和都等于20049.
第三步，分段的列变换.
基方阵A上方3×9方阵A1，下方3×9方阵A3做列交换得方阵B，列变换的方式由方阵B中浅灰格显示，如图18-12所示.
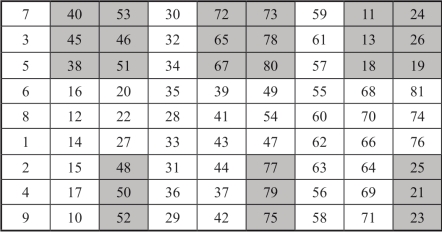
图18-12 方阵B
第四步，方阵B各行顺移得方阵C，顺移的方式由方阵C中浅灰格显示，如图18-13所示.
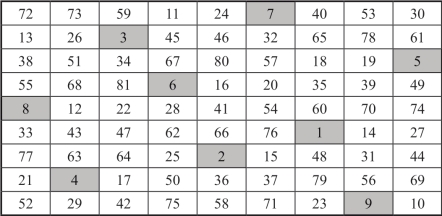
图18-13 方阵C
方阵C是一个9阶二次幻方，其本身是一个对称幻方，幻方常数为369，各个数字平方后所得幻方的幻方常数为20049.为了让读者有一个清晰的印象，各个数字平方后所形成的幻方如图18-14所示.
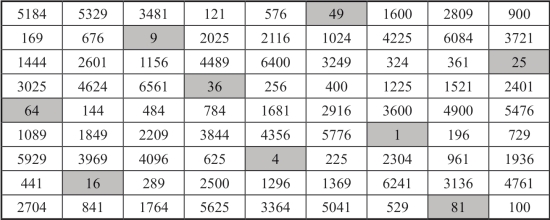
图18-14 二次幻方C各个数字平方后所形成的幻方
用类似的方法可以得到多少个不同的9阶二次幻方？(www.chuimin.cn)
由9阶二次幻方C，通过把上方三行整体平移至底部，就产生另一个9阶二次幻方D，如图18-15所示.
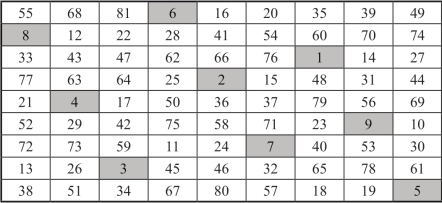
图18-15 9阶二次幻方D
9阶二次幻方D各个数字平方后所形成的幻方如图18-16所示.
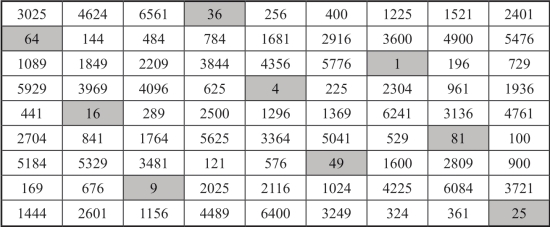
图18-16 二次幻方D各个数字平方后所形成的幻方
由9阶二次幻方D，通过把上方三行整体平移至底部，就产生不同的又一个9阶二次幻方E，如图18-17所示.
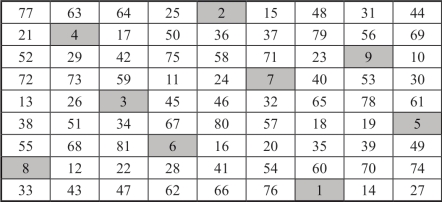
图18-17 9阶二次幻方E
由9阶二次幻方C，通过把左方三列整体平移至右方，就产生不同的另一个9阶二次幻方F，如图18-18所示.
图18-18 9阶二次幻方F
由9阶二次幻方F，通过把左方三列整体平移至右方，就产生不同的又一个9阶二次幻方G，如图18-19所示.
图18-19 9阶二次幻方G
对9阶二次幻方D，9阶二次幻方E作类似于对9阶二次幻方C所作的右移可得另外4个不同的9阶二次幻方，你能写出并验证它们确是9阶二次幻方吗？这里共得到了9个9阶二次幻方.还能得到更多的9阶二次幻方吗？
能.若第一步时我们选取不同的3×3方阵则可得出另外9个9阶二次幻方，为免赘述起见我们只列出一个9阶二次幻方构造过程的图形而不再重复那些说明.
第一步，寻找构成基方阵A的3个3×9方阵.
⑴
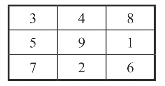
图18-20 3×3的方阵
图18-21 1×9的方阵
图18-22 衍生的3×9方阵
图18-23 构成基方阵A的3×9方阵A1
⑵
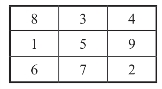
图18-24 3×3的方阵
图18-25 衍生的3×9方阵
图18-26 构成基方阵A的3×9方阵A2
⑶
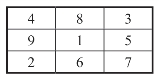
图18-27 3×3的方阵
图18-28 衍生的3×9方阵
图18-29 构成基方阵A的3×9方阵A3
第二步，
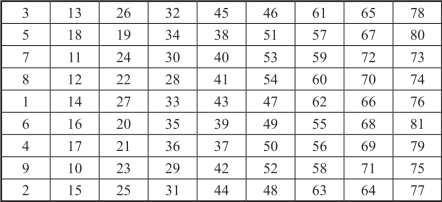
图18-30 基方阵A
第三步，
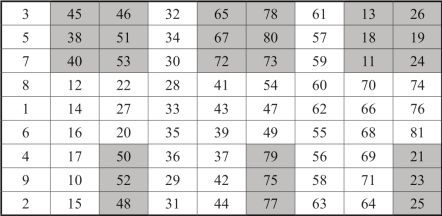
图18-31 方阵B
第四步，
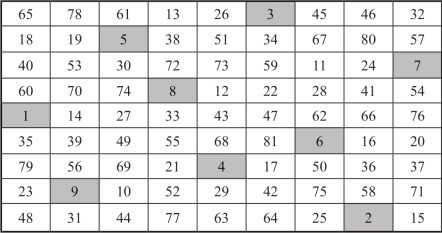
图18-32 9阶二次幻方H
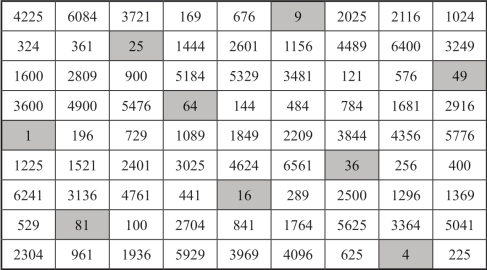
图18-33 二次幻方H各个数字平方后所形成的幻方
第一步时我们有6种不同的选取3×3方阵的方法，所以我们可得到6×9=54个不同的9阶二次幻方.你能造出一个与上述不同的9阶二次幻方并验证它们确是9阶二次幻方吗？更进一步地除了上述6种不同的选取3×3方阵的方法外还有其他的选取具有同样特性的3×3方阵的方法，这些3×3方阵用类似的方法能造出9阶二次幻方吗？试试看并记得加以验证.在这个过程中你一定会感受到正在攀登幻方领域高峰的快感与乐趣的.
有关幻中之幻的文章
- 详细阅读
-
幻中之幻：构造9阶空间对称幻立方的方法详细阅读
第一步，根据文[1]中构造对称幻方的两步法，构造一个由1～81的自然数组成的9阶对称幻方的基方阵A，按自然数的顺序安装各列基数随后的8个数，得基方阵A如图12-27所示.图12-27基方阵A记基方阵A位于第i行第j列的元素为a（i，j）其中i，j＝1，2，…B9的基数及基方阵B3，B4，…））2=18432个不同的9阶对称幻方，它们来自18432个不同的9阶基方阵，由这些不同的9阶基方阵出发就可分别得出同样数目的不同9阶空间对称的幻立方.......
2023-10-20
-
同基因8阶二次兼完美幻方的产生幻中之幻详细阅读
任何一个8阶二次兼完美幻方都可以以下四组共16个（包括其本身）对称变换各得到一个同基因的8阶二次兼完美幻方：为方便起见，标志①～⑧依次表示已知的8阶二次兼完美幻方的第1行至第8行，以从左到右的顺序表示其在新幻方中的行数.四组对称变换如下，在以下每一个行变换后，列亦要做同样的对称变换.Ⅰ.⑴①②③④ ⑤⑥⑦⑧⑵④③②① ⑧⑦⑥⑤⑶①③②④ ⑤⑦⑥⑧⑷④②③① ⑧⑥⑦⑤Ⅱ.⑴②①④③ ⑥⑤⑧⑦⑵③④①......
2023-10-20
-
4阶最完美幻方：幻中之幻详细阅读
第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2023-10-20
-
阶完美或对称完美的砍尾巴幻方：幻中之幻详细阅读
）2=2=518400个不同的7阶幻方，7阶完美幻方.48·8=384个不同的7阶对称完美幻方.显然由两步法得到的7阶砍尾巴幻方、7阶完美的砍尾巴幻方，7阶对称完美的砍尾巴幻方比原先得到的幻方，完美幻方，对称完美幻方多得多.......
2023-10-20
-
21阶对称完美幻方的构造方法：幻中之幻详细阅读
，21），以c（i，j）记方阵C位于第i行第j列的元素（其中i，j=1，2，…，21）.取c（i，j）=·21（其中i，j=1，2，…......
2023-10-20
-
奇数阶空间对称完美幻立方：幻中之幻详细阅读
的自然数）阶空间对称完美幻立方的三步法[10]：第一步，按文[1]构造奇数n=2m+1（m为m≠3t+1t＝0，1，2，…的自然数）阶对称完美幻方方法的第一步，构造n×n基方阵A.基方阵A位于第i行，第j列的元素为a（i，j）（i，j=1，2，…，n-1第三步，与构造空间完美幻立方步骤的第三步相同，即第k个截面的基方阵Bk第i行的元素按余函数r的规则右移r（i=1，2，…的自然数）阶空间对称完美幻立方.......
2023-10-20
-
阶最完美幻方->幻中之幻：8阶完美幻方详细阅读
第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.注意到1～8的自然数列中处于“中心”对称位置上的两个自然数，其和都等于8+1=9，我们共有4对这样的自然数1，8；2，7；3，6和4，5，在每对自然数中随意选取一个自然数，将这4个自然数随意排序，余下的4个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于8+1=9.比如我们取7，3，4，8，1，5，6，2这样的顺序，相应的自......
2023-10-20
相关推荐