从1～9的自然数中任意选定5个数，比如1，3，6，5，8，它们的和是23.任意选定另外5个数，使它们的和亦是23，比如9，2，7，1，4.1，3，6，5，8，各取5次，仿照构造完美幻方的两步法[1]，得到一个不连续数的五阶完美幻方，其幻方常数为是23.其基方阵如图2-12所示，所得不连续数的5阶完美幻方，如图2-13所示.图2-125阶基方阵图2-13不连续数的5阶完美幻方9，2，7，1，4.......
2023-10-20
21阶对称完美幻方的构造方法：幻中之幻
【摘要】：，21），以c（i，j）记方阵C位于第i行第j列的元素（其中i，j=1，2，…，21）.取c（i，j）=·21（其中i，j=1，2，…
第一步，把1～21的自然数排成三行7列，使每行7个数字之和都等于77，3×7长方阵如图10-6所示.
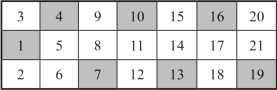
图10-6 3×7长方阵
把各行的7个数字随意排序，比如第一行的7个数字从左到右按4，3，10，20，16，15，9排列，称为基本行1；第二行的7个数字从左到右按5，1，11，21，17，14，8排列，称为基本行2；第三行的7个数字从左到右按6，2，12，19，18，13，7排列，称为基本行3.若排成一个3×7长方阵如图10-7所示.
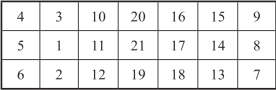
图10-7 由基本行组成的3×7长方阵
第二步，构造21阶对称的基方阵A.
从左到右依次取基本行1：4，3，10，20，16，15，9共三次作为基方阵A的第一行，第一行的元素向左顺移两个位置得第二行，第二行的元素向左顺移两个位置得第三行，依此类推直至得出第7行.
从左到右依次取基本行2：5，1，11，21，17，14，8共三次作为基方阵A的第8行，第8行的元素向左顺移两个位置得第9行，第9行的元素向左顺移两个位置得第10行，依此类推直至得出第14行.
从左到右依次取基本行3：6，2，12，19，18，13，7共三次作为基方阵A的第15行，第15行的元素向左顺移两个位置得第16行，第16行的元素向左顺移两个位置得第17行，依此类推直至得出第21行.
21阶对称的基方阵A如图10-8所示.
图10-8 对称的基方阵A
第三步，做对称的基方阵A的转置方阵B.对称的转置方阵B如图10-9所示.
(www.chuimin.cn)
图10-9 对称的转置方阵B
第四步，做对称的方阵C.
以b（i，j）记转置方阵B位于第i行第j列的元素（其中i，j=1，2，…，21），
以c（i，j）记方阵C位于第i行第j列的元素（其中i，j=1，2，…，21）.
取c（i，j）=（b（i，j）－1）·21（其中i，j=1，2，…，21）.
对称的方阵C如图10-10所示.
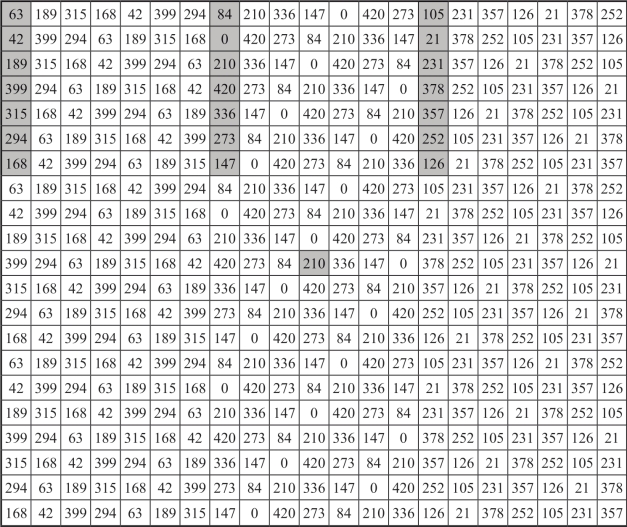
图10-10 对称的方阵C
第五步，对称的基方阵A与对称的方阵C对应元素相加所得的对称方阵D，就是一个21阶对称完美幻方如图10-11所示.
图10-11 21阶对称完美幻方
图10-11是一个由1～441的自然数组成的21阶对称完美幻方，其幻方常数为4641.每行每列上21个数字之和都等于4641，对角线或泛对角线上21个数字之和亦都等于4641.中心对称位置上两个数字之和都等于442.
有兴趣的读者可把图10-7由基本行组成的3×7长方阵各行都向右顺移一个位置得一个新的3×7数字长方阵，观察其有什么特点，你将会从中领会到如何选定基本行才可使基方阵A成为一个对称方阵，进而通过五步法得到一个属于你自己的21阶正规的对称完美幻方.
有关幻中之幻的文章
- 详细阅读
-
构造完美7阶幻方-幻中之幻详细阅读
第一步，由构造对称完美幻方的两步法[1]得到的一个7阶对称完美幻方，其幻方常数是175.中心对称位置上两个元素之和都等于50.其基方阵A如图5-9所示，7阶对称完美幻方如图5-10所示.图5-97阶基方阵A图5-107阶对称完美幻方上述7阶对称完美幻方其所有数都加10，得一个新的由11～59的自然数组成的非正规的7阶对称完美幻方B，如图5-11所示.图5-11非正规的7阶对称完美幻方B第二步......
2023-10-20
-
阶完美或对称完美的砍尾巴幻方：幻中之幻详细阅读
）2=2=518400个不同的7阶幻方，7阶完美幻方.48·8=384个不同的7阶对称完美幻方.显然由两步法得到的7阶砍尾巴幻方、7阶完美的砍尾巴幻方，7阶对称完美的砍尾巴幻方比原先得到的幻方，完美幻方，对称完美幻方多得多.......
2023-10-20
- 详细阅读
-
4阶最完美幻方：幻中之幻详细阅读
第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2023-10-20
-
阶最完美幻方->幻中之幻：8阶完美幻方详细阅读
第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.注意到1～8的自然数列中处于“中心”对称位置上的两个自然数，其和都等于8+1=9，我们共有4对这样的自然数1，8；2，7；3，6和4，5，在每对自然数中随意选取一个自然数，将这4个自然数随意排序，余下的4个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于8+1=9.比如我们取7，3，4，8，1，5，6，2这样的顺序，相应的自......
2023-10-20
-
构造12阶最完美砍尾幻方，惊叹幻中之幻！详细阅读
按构造双偶数阶最完美幻方的三步法先构造一个12阶最完美幻方，再仿照同一个三步法构造一个由尾数组成的12阶最完美幻方，两个幻方对应的元素结合所得就是一个12阶最完美的砍尾巴幻方.构造12阶最完美幻方的过程如图4-13，图4-14和图4-15所示.图4-1312阶基方阵A图4-14行变换后所得方阵B图4-1512阶最完美幻方图4-15是一个正规的12阶最完美幻方，其每一行，每一列上的12个数字之......
2023-10-20
-
7阶空间完美幻立方的构造方法：幻中之幻详细阅读
，7）个截面.⑴⑵⑶⑷⑸⑹⑺图14-25以i轴为法线方向的7个截面表示的7阶空间完美幻立方图14-18至图14-24表示的数字立方阵C与图14-25是同一个空间完美幻立方.图14-25中各个截面的列就是数字立方阵C所表示的空间完美幻立方的纵列.上述三步法中第一步有（7！......
2023-10-20
相关推荐