自己动手试一试，探索一下如何？注意，用于构造每一个7阶非正规完美幻方的各组的数字，在安装基方阵时处于何列是随意的，7阶非正规完美幻方B1，B2，B3，B4和B5随意组合所得亦是一个7×35的完美幻矩形.那么借助构造完美幻方的两步法我们能构造出多少个不同的7×35的完美幻矩形，你能算出这个数目吗？为便于读者阅读，第一步中给出的组序号的长方形是最简单的，其一般形式在本章第三节中给出.......
2023-10-20
完美幻矩形：幻中之幻
【摘要】：如何构造×的完美幻矩形，其中m为m≠3t+1t=0，1，2，…，2m-1）取遍1～的自然数，取与上述×的长方阵，第i行的元素a（i，j）（j=1，2，…，2m+1）对应组的数，即第a（i，j）（j=1，2，…）个不同的×的完美幻矩形.
如何构造（2m+1）×（2m－1）（2m+1）的完美幻矩形，其中m为m≠3t+1 t=0，1，2，…的自然数.这个完美幻矩形由从左到右2m-1个2m+1阶完美幻方组合而成.
第一步，把1～（2m-1）（2m+1）2的自然数按从小到大均分为（2m-1）（2m+1）组，为确定从左到右各个（2m+1）阶完美幻方都各由那几组数构成，把各组的序号按特定的方式排成一个（2m-1）×（2m+1）的长方阵，记其位于第i行，第j列的元素为a（i，j）（i=1，2，…，2m-1；j=1，2，…，2m+1）
a(i,j)=(2m-1)·cj+dr(m-1+(i+j))(i,j=1,2,…,2m-1)
a(i,2m)=(2m-1)·c2m+dr(m+i)（i=1,2,…,2m-1）
a(i,2m+1)=(2m-1)·c2m+1+dr(m-i)（i=1,2,…,2m-1）
其中r（t）为余函数，
（n=2m-1，m，t是自然数，t|n表示t被n整除，q（t）表示t除以n的余数）(www.chuimin.cn)
Cj（j=1，2，…，2m+1）取遍0～2m的自然数，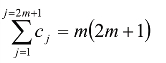
dk（k=1，2，…，2m-1）取遍1～（2m－1）的自然数，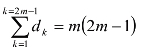
取与上述（2m－1）×（2m+1）的长方阵，第i行的元素a（i，j）（j=1，2，…，2m+1）对应组的数，即第a（i，j）（j=1，2，…，2m+1）组的数，按照构造完美幻方的两步法构造从左到右第i（i=1，2，…，2m-1）个完美幻方.
第二步，把第一步得到的2m－1个2m+1阶完美幻方，随意组合就是一个的完美幻矩形.
还要提及的是构造完美幻方的两步法中关于基方阵A中间一列的限制是完全没有必要的，所以借助构造完美幻方的两步法我们应能构造出（（2m-1）！）·（（2m）！）·（（2m+1）！）个不同的（2m+1）×（2m-1）（2m+1）的完美幻矩形.
有关幻中之幻的文章
- 详细阅读
- 详细阅读
-
构造完美的4×8幻矩形：幻中之幻详细阅读
这个最完美幻矩形由左，右两个4阶最完美幻方组合而成.第一步，把1～32的自然数按从小到大均分为8组，按从小到大的顺序把每组的第一个数排列如图7-1所示.图7-1取第1，2和第7，8组的数，按照构造最完美幻方的三步法构造左边那个最完美幻方.此处各组的数字是按自然数顺序排列的.基方阵A1如图7-2所示，基方阵A1行变换后所得方阵B1如图7-3所示，而4阶非正规最完美幻方C1如图7-4所示.图7-24......
2023-10-20
- 详细阅读
- 详细阅读
-
《幻中之幻》：奇数阶完美幻立方详细阅读
的自然数）阶空间完美幻立方的三步法[10]：第一步，按文[11]构造奇数n=2m+1（m为m≠3t+1t=0，1，2，…的自然数）阶完美幻方方法的第一步，构造n×n基方阵A.基方阵A位于第i行，第j列的元素为a（i，j）（i，j=1，2，…）2种不同的选择，其第二步各列基数及随后共n个数的安装顺序有n！的自然数）阶空间完美幻立方.......
2023-10-20
- 详细阅读
-
奇数阶空间对称完美幻立方：幻中之幻详细阅读
的自然数）阶空间对称完美幻立方的三步法[10]：第一步，按文[1]构造奇数n=2m+1（m为m≠3t+1t＝0，1，2，…的自然数）阶对称完美幻方方法的第一步，构造n×n基方阵A.基方阵A位于第i行，第j列的元素为a（i，j）（i，j=1，2，…，n-1第三步，与构造空间完美幻立方步骤的第三步相同，即第k个截面的基方阵Bk第i行的元素按余函数r的规则右移r（i=1，2，…的自然数）阶空间对称完美幻立方.......
2023-10-20
相关推荐