第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.第1列按自上而下的顺序安装自然数1～8，第2列按自下而上的顺序安装自然数9～16，第3列按自上而下的顺序安装自然数17～24，第4列按自下而上的顺序安装自然数25～32；第8列按自下而上的顺序安装自然数33～40，第7列按自上而下的顺序安装自然数41～48，第6列按自下而上的顺序安装自然数49～56，第5列按自上而下的顺序安装自然数57～6......
2025-09-30
阶完美或对称完美的砍尾巴幻方：幻中之幻
【摘要】：）2=2=518400个不同的7阶幻方，7阶完美幻方.48·8=384个不同的7阶对称完美幻方.显然由两步法得到的7阶砍尾巴幻方、7阶完美的砍尾巴幻方，7阶对称完美的砍尾巴幻方比原先得到的幻方，完美幻方，对称完美幻方多得多.
你很自然会想到，要构造一个7阶完美或对称完美的砍尾巴幻方必须先构造一个7阶完美或对称完美幻方，再仿照同一个两步法构造一个由尾数组成的完美或对称完美幻方，两个幻方对应的元素结合所得就是一个7阶完美或对称完美的砍尾巴幻方.
由构造对称完美幻方的两步法[]1得到的一个7阶对称完美幻方，其幻方常数是175.中心对称位置上两个元素之和都等于50.其基方阵A如图3-1所示，对称完美幻方如图3-2所示.
图3-1 7阶基方阵A
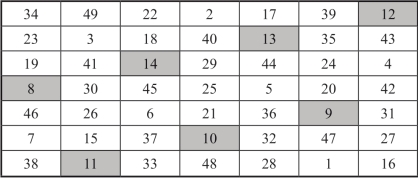
图3-2 7阶对称完美幻方
从1～9的自然数任意选定7个数，比如1，1，2，3，4，5，6各取7次，仿照构造完美幻方的两步法，得到一个由7组相同数字组成的7阶完美幻方，其幻方常数是22.其基方阵如图3-3所示，完美幻方如图3-4所示.
图3-3 7阶基方阵A
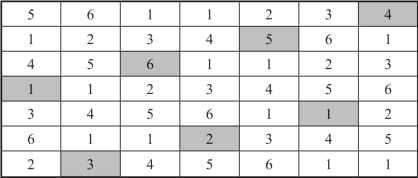
图3-4 7组相同数字组成的7阶完美幻方
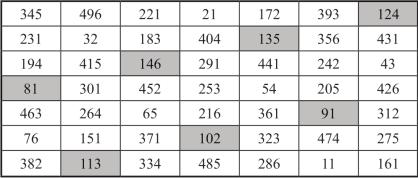
把图3-4的数字作为新幻方的个位数，图3-2相应位置上数字的个位数作为新幻方的十位数，而其十位数作为新幻方的百位数，图3-4与图3-2结合所得就是一个7阶完美的砍尾巴幻方，如图3-5所示.
(https://www.chuimin.cn)
图3-5 7阶完美的砍尾巴幻方
图3-5是一个幻方常数为1772的7阶完美砍尾巴幻方，砍尾巴后所得方阵图3-2是一个幻方常数为175的由自然数1～49组成的7阶对称完美幻方.
组成图3-4的数1，1，2，3，4，5，6是从1～9的自然数中可重复地随意抽取的.如果想造出一个7阶对称完美砍尾巴幻方，这7个数必须是中心对称的数列（即处于中心对称位置上的两个数其和都是中位数的2倍），最简单的情形是取7个连续的自然数，比如我们选2，3，4，5，6，7，8，仿照构造对称完美幻方的两步法，得到一个由7组相同数字组成7阶对称完美幻方，其幻方常数是35.其基方阵如图3-6所示，对称完美幻方如图3-7所示.
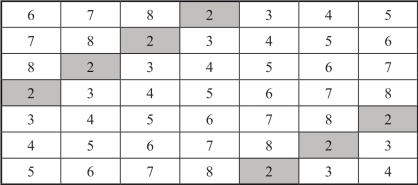
图3-6 7阶基方阵A
图3-7 7组相同数字组成的7阶对称完美幻方
把图3-7的数字作为新幻方的个位数，图3-2相应位置上数字的个位数作为新幻方的十位数，而其十位数作为新幻方的百位数，图3-7与图3-2结合所得就是一个7阶对称完美的砍尾巴幻方，如图3-8所示.
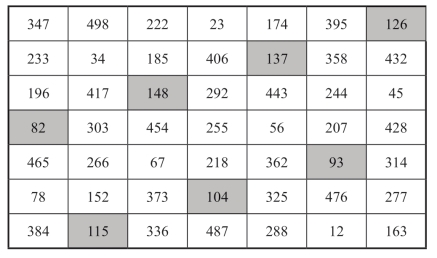
图3-8 7阶对称完美的砍尾巴幻方
图3-8是一个幻方常数为1785的7阶对称完美砍尾巴幻方，中心对称位置上两个元素之和都等于510.砍尾巴后所得方阵图3-2是一个幻方常数为175的由自然数1～49组成的7阶对称完美幻方.
用两步法可构造出（（6·5·4·3·2·1）！）2=（720）2=518400个不同的7阶幻方，7阶完美幻方.48·8=384个不同的7阶对称完美幻方.显然由两步法得到的7阶砍尾巴幻方、7阶完美的砍尾巴幻方，7阶对称完美的砍尾巴幻方比原先得到的幻方，完美幻方，对称完美幻方多得多.
相关文章
- 详细阅读
-
4阶最完美幻方：幻中之幻详细阅读
第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2025-09-30
-
12阶最完美幻方-幻中之幻详细阅读
第一步，安装12阶基方阵A.把1～144按从小到大均分为12组.注意到1～12的自然数列中处于“中心”对称位置上的两个自然数，其和都等于12+1=13，我们共有6对这样的自然数1，12；2，11；3，10；4，9；5，8和6，7，在每对自然数中随意选取一个自然数，将这6个自然数随意排序，余下的6个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于12+1=13.比如我们取5，7，10......
2025-09-30
-
佚名作者易位幻方：幻中之幻详细阅读
以下是《幻方及其他》一书中给出的易位幻方：图2-1佚名作者的易位幻方图2-2易位后的幻方人们对事物的认知都是建立在前人经验的基楚上的，为要找出构造易位幻方的方法，注意图2-1是一个最完美幻方，其幻方常数为242.特点是其每一行，每一列或每一条对角线或泛对角线上四个数的十位数之和都等于22，个位数之和亦都等于22.每一条对角线或泛对角线上间距两个位置的两个数字十位数之和都等于11，个位数之和亦都......
2025-09-30
-
平面幻中之幻：揭秘第一部分成果详细阅读
“平面的幻中之幻”与《你亦可以造幻方》（丛书“棘手而又迷人的数学”，科学出版社，2012.3）一起，系统地解决了平面主要类型幻方如何构造的问题.当然，其中一些存在或不排除存在其他方法，但许多是在这里第一次得到了解决.《你亦可以造幻方》一书中除了奇数阶基本幻方外，其他幻方由于对称性，完美性及更多的其他特性已可称为幻中之幻.本部分第一章讲述的最完美幻方顾名思义自然就是幻中之幻的瑰宝，而其他各章讲述的神......
2025-09-30
-
不完美的人才是完美人详细阅读
朋友陈红这几年过得不顺心，我想间接地给予她帮助，便邀请陈红跟我一起听励志讲座，这次讲座的主讲者是世界上最成功的励志大师之一。我问陈红，是否真的觉得那人很失败。在纸的背面，我写下了陈红的情况。陈红看完对比，脸煞白根本不愿开口说话，因为这样的对比无疑说明她是一个失败者，这触动了她最脆弱的神经。意识到了这一点之后，陈红终于能够接受自己作为失败者的一面，放下心中的包袱，开始新的生活。......
2025-09-29
-
如真似幻：探析电视剧文化详细阅读
为了有效管理影视剧的制作，在20世纪20年代出现了“制片人制”，这是一种电影工业流水线生产的管理模式。影视剧生产的制片人制就是以制片人为中心的一种管理体制，制片人具有很大的权力，掌控影视剧生产、经营的全过程，以便实现预定的盈利目标。对电视剧生产商来说，他的客户主要是电视台和网络播放平台。电视剧作为文化产品，在生产和消费上与工业品有很大的不同。电视剧的知识产权保护是确保电视剧生产者利益的非常重要的措施。......
2025-09-29
-
赏析电视剧文化如真似幻详细阅读
而到了90后这一代，聚在一起看电视剧的情形已经很少出现，他们往往是自己一个人在有空的时候看，不过大家仍会就电视剧收看感受进行交流，网络社区成了他们交流的主要平台。在针对大学生的一项调查中笔者发现，90后男生看电视剧要比女生少很多，有多名男生表示自己平时并不怎么看电视剧。90后对于韩剧、日剧和美剧都有比较多的接触，他们通过网络渠道观看电视剧，收看方式与老一辈有很大的区别。......
2025-09-29
相关推荐