第一步，安装12阶基方阵A.把1～144按从小到大均分为12组.注意到1～12的自然数列中处于“中心”对称位置上的两个自然数，其和都等于12+1=13，我们共有6对这样的自然数1，12；2，11；3，10；4，9；5，8和6，7，在每对自然数中随意选取一个自然数，将这6个自然数随意排序，余下的6个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于12+1=13.比如我们取5，7，10......
2025-09-30
7阶易位完美幻方构造方法
【摘要】：从1～9的自然数中任意选定7个数，比如7，5，8，6，3，1，2，它们的和是32.任意选定与上述7个数不完全相同的7个数，使它们的和亦是32，比如6，9，2，3，7，1，4.7，5，8，6，3，1，2，各取7次，仿照构造完美幻方的两步法，得到一个不连续数的7阶完美幻方，幻方常数是32.其基方阵如图2-20所示，所得不连续数的7阶完美幻方，如图2-21所示.图2-207阶基方阵图2-21不连续数
从1～9的自然数中任意选定7个数，比如7，5，8，6，3，1，2，它们的和是32.
任意选定与上述7个数不完全相同的7个数，使它们的和亦是32，比如6，9，2，3，7，1，4.
7，5，8，6，3，1，2，各取7次，仿照构造完美幻方的两步法，得到一个不连续数的7阶完美幻方，幻方常数是32.其基方阵如图2-20所示，所得不连续数的7阶完美幻方，如图2-21所示.
图2-20 7阶基方阵
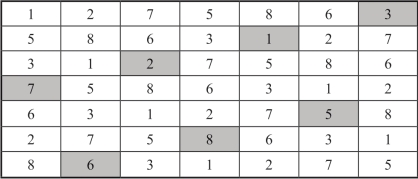
图2-21 不连续数的7阶完美幻方
6，9，2，3，7，1，4，各取7次，仿照构造完美幻方的两步法，得到另一个不连续数的7阶完美幻方，幻方常数是32.其基方阵如图2-22所示，所得不连续数的7阶完美幻方，如图2-23所示.
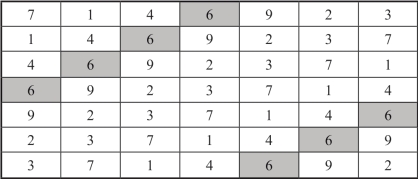
图2-22 7阶基方阵
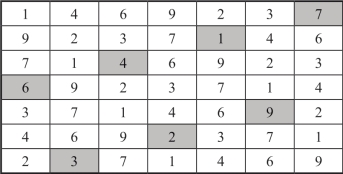
图2-23 不连续数的7阶完美幻方(https://www.chuimin.cn)
以图2-23的列作为行得另一个不连续数的7阶完美幻方，如图2-24所示.
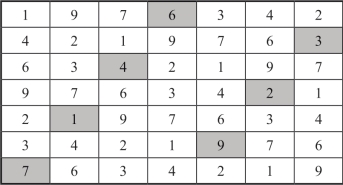
图2-24 不连续数的7阶完美幻方
把图2-21完美幻方中的数作为新幻方中两位数的十位数，图2-24完美幻方中相应位置上的数作为新幻方中两位数的个位数，得幻方常数为352的易位幻方.其每一行，每一列或每一条对角线或泛对角线上7个数之和都等于352.其每一行，每一列或每一条对角线或泛对角线上7个数的十位数之和以及个位数之和都等于32.它是一个易位完美幻方，如图2-25所示，易位后仍是一个完美幻方如图2-26所示.
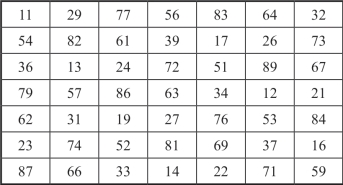
图2-25 幻方常数为352的7阶易位完美幻方
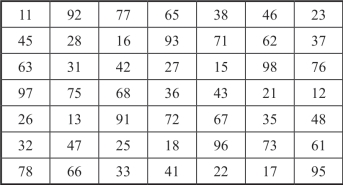
图2-26 易位后的完美幻方
注意，图2-21是仿照构造完美幻方的两步法对特殊数组构造的7阶完美幻方，而图2-23是仿照构造完美幻方的两步法对特殊数组构造的另一个7阶完美幻方，而图2-24以图2-23的列作为行，所得的易位完美幻方中就不会出现重复的数字.如果直接由图2-21与图2-23复合，期望进而得出易位幻方，结果只会是一个由重复数字组成的毫无意义的数字方阵.
你会构造更多的7阶易位完美幻方了吗？
相关文章
- 详细阅读
-
4阶最完美幻方：幻中之幻详细阅读
第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2025-09-30
-
构造双偶数最完美幻方的步骤详细阅读
，2m）.令cj=j-1，j=1，2，…，4m.对于第j列，若j为奇数，自上而下按ncj+dk（k＝1，2，…，n）的顺序安装相继的数至该列最下面的第n行；若j为偶数，自下而上按ncj+dk（k＝1，2，…）个不同的双偶数n=4m（m=1，2…为自然数）阶最完美幻方，其左半部分2m列中，任意选取若干列各自与与其相距2m列的相应列做列交换，所得仍是一个n=4m（m=1，2…为自然数）阶最完美幻方.......
2025-09-30
-
最完美的8阶最简单幻方—幻中之幻详细阅读
第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.第1列按自上而下的顺序安装自然数1～8，第2列按自下而上的顺序安装自然数9～16，第3列按自上而下的顺序安装自然数17～24，第4列按自下而上的顺序安装自然数25～32；第8列按自下而上的顺序安装自然数33～40，第7列按自上而下的顺序安装自然数41～48，第6列按自下而上的顺序安装自然数49～56，第5列按自上而下的顺序安装自然数57～6......
2025-09-30
-
佚名作者易位幻方：幻中之幻详细阅读
以下是《幻方及其他》一书中给出的易位幻方：图2-1佚名作者的易位幻方图2-2易位后的幻方人们对事物的认知都是建立在前人经验的基楚上的，为要找出构造易位幻方的方法，注意图2-1是一个最完美幻方，其幻方常数为242.特点是其每一行，每一列或每一条对角线或泛对角线上四个数的十位数之和都等于22，个位数之和亦都等于22.每一条对角线或泛对角线上间距两个位置的两个数字十位数之和都等于11，个位数之和亦都......
2025-09-30
-
踏步和栏杆扶手的构造方法详细阅读
图10.17踏步防滑条构造2）栏杆与扶手构造楼梯的防护构件是栏杆和扶手，通常设置于楼梯段和平台临空一侧，三股人流时两侧设扶手，四股人流时加中间扶手。图10.18透空式扶手方钢截面边长与圆钢的直径一般为15～25mm，栏杆钢条花格的间隙对居住建筑或儿童使用的楼梯均不宜超过110mm，同时为防止儿童攀爬，不应设水平横杆。图10.19钢化玻璃栏杆常用的楼梯栏杆多为钢构件，包括圆钢、钢管、方钢、扁钢等的组合。......
2025-09-30
-
提升二阶系统性能的方法探讨详细阅读
通过对二阶系统的分析可知，适当调整系统的阻尼比ζ和自然振荡频率ωn可以改善系统的动态性能，但是改善效果有限。图3-17二阶系统的微分负反馈控制系统的开环传递函数为系统的闭环传递函数为称ζk为等效阻尼比，即系统的误差传递函数为根据拉氏变换终值定理，可得由上可知，二阶系统在增加微分负反馈控制后，系统性能改善有以下3个方面。......
2025-09-29
-
划分子网和构造超网的方法详细阅读
在一个网络内划分出的网络称为子网。如果一个网络不划分子网，则子网掩码为默认子网掩码。例如，“202.117.68.0/18”表示前18 位是网络号和子网号，主机号14 位。给出采用VLSM 划分子网的过程。将原来的C 类地址，用主机号字段的1 位进行子网划分，产生两个子网，即202.117.144.0/25和202.117.144.128/25。拟选择202.117.144.160/27 作为部门乙的子网，202.117.144.192/27 作为部门丙和部门丁的子网继续进行划分。......
2025-09-30
相关推荐