为自然数）阶最完美幻方的三步法构造一个双偶数n=4m（m=1，2，…为自然数）阶最完美幻方.由于从1～9的自然数中可重复地任意选定其和相等的2m对数，作为尾数，每对尾数的和可从2～18中任意选择，比如选定其和为10，则尾数有92m种不同的选择，即每一个双偶数n=4m（m=1，2，…）个的不同的n=4m（m=1，2，…......
2023-10-20
构造双偶数最完美幻方的步骤
【摘要】：，2m）.令cj=j-1，j=1，2，…，4m.对于第j列，若j为奇数，自上而下按ncj+dk（k＝1，2，…，n）的顺序安装相继的数至该列最下面的第n行；若j为偶数，自下而上按ncj+dk（k＝1，2，…）个不同的双偶数n=4m（m=1，2…为自然数）阶最完美幻方，其左半部分2m列中，任意选取若干列各自与与其相距2m列的相应列做列交换，所得仍是一个n=4m（m=1，2…为自然数）阶最完美幻方.
第一步，安装n＝4m（m＝1，2，…为自然数）阶基方阵A.
注意到1～n的自然数列中处于“中心”对称位置上的两个自然数，其和都等于n+1，我们共有2m对这样的自然数，在每对自然数中随意选取一个自然数，将这2m个自然数随意排序依次记为dk（k＝1，2，…，2m），余下的2m个自然数记为dn-k+1（k＝1，2，…，2m），但必须满足条件dk+dn-k+1=n+1（k=1，2，…，2m）.
令cj=j-1，j=1，2，…，2m；cj=6m-j，j=2m+1，…，4m.对于第j列，若j为奇数，自上而下按ncj+dk（k＝1，2，…，n）的顺序安装相继的数至该列最下面的第n行；若j为偶数，自下而上按ncj+dk（k＝1，2，…，n）的顺序安装相继的数至该列最上面的第1行；所得到的n阶方阵叫作基方阵A，基方阵A的每一行数字之和都等于幻方常数
.
第二步，对基方阵A做行变换，基方阵A上半部分不变，第2m+1～4m行依次作为新方阵的第4m～2m+1行，所得方阵记为B.
第三步，方阵C偶数行左右两部分交换所得方阵记为C，n阶方阵C就是一个n阶最完美幻方.
n阶方阵C每一行，每一列上的n个数字之和都等于幻方常数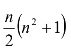
，对角线或泛对角线上n个数之和亦都等于
，对角线或泛对角线上，间距为2m个位置的2个数字之和都等于（n2+1）；任意位置上截取一个2×2的小方阵，其中4数之和都等于2（n2+1），所以方阵C是一个n=4m（m=1，2…为自然数）阶最完美幻方.(www.chuimin.cn)
用三步法可构造出22m（（2m）！）个不同的双偶数n=4m（m=1，2…为自然数）阶最完美幻方.不包括由每一个n=4m（m=1，2…为自然数）阶最完美幻方衍生出的n2个（包括这个n=4m阶最完美幻方）n=4m阶最完美幻方.
注意到每一个由三步法得到的n=4m（m=1，2…为自然数）阶最完美幻方，其左半部分2m列中，任意选取若干列各自与与其相距2m列的相应列做列交换，所得仍是一个n=4m（m=1，2…为自然数）阶最完美幻方.即得出22m－1个不同的n=4m阶最完美幻方（包括这个n=4m阶最完美幻方）.
又注意到每一个由三步法得到的n=4m阶最完美幻方，其左半部分2m列在左半部分中向右顺移，右半部分亦做相应的右移，所得仍是一个n=4m阶最完美幻方，即得出2m个不同的n=4m阶最完美幻方（包括这个n=4m阶最完美幻方）.
所以由三步法实际上可构造出22m（（2m）！）（22m-1）（2m）个不同的n=4m（m=1，2…为自然数）阶最完美幻方.
有关幻中之幻的文章
- 详细阅读
-
构造12阶最完美幻方详细阅读
第一步，构造一个12阶最完美幻方的过程如图6-10，图6-11和图6-12所示.图6-1010阶基方阵A图6-11行变换后所得方阵图6-1212阶最完美幻方上述12阶最完美幻方其所有数都加100，得一个新的由101～244的自然数组成的非正规的12阶最完美幻方B，如图6-13所示.图6-13非正规的12阶最完美幻方B第二步，从1～9的自然数中任意选定其和相等的六对数，比如7与2，8与1，1......
2023-10-20
-
构造最完美的幻方:双偶数n=4m阶幻中之幻详细阅读
为自然数）阶最完美幻方.由于从1～9的自然数中可重复地任意选定其和相等的2m对数，作为尾数，每对尾数的和可从2～18中任意选择，比如选定其和为10，则尾数有92m种不同的选择，同理每对首位数如选定其和为10，则首位数亦有92m种不同的选择.即每一个双偶数n=4m（m=1，2，…为自然数）阶最完美的掐头去尾幻方，亦即利用构造双偶数n=4m（m=1，2，…）个不同的n=4m（m=1，2，…......
2023-10-20
-
构造8阶易位最完美幻方的方法详细阅读
你应已猜到可以仿照构造最完美幻方的三步法去得到4阶易位最完美幻方.至于9阶或9阶以上易位幻方的构造，似乎可以利用上述方法去解决，但作者要指出的是，所得方阵会出现重复数字，乏味得很.作者想要告诉读者的是，当你遇到一个你感兴趣的幻方，在该类幻方的构造方法上，不论前人或别人已做到什么程度，你仍然可以按照自己的思路去探索，而必有所得，根据你对自己提出的不同层次的要求，得出不同层次的成果.......
2023-10-20
-
如何构造8阶最完美砍尾巴幻方详细阅读
按构造双偶数阶最完美幻方的三步法先构造一个8阶最完美幻方，再仿照同一个三步法构造一个由尾数组成的8阶最完美幻方，两个幻方对应的元素结合所得就是一个8阶最完美的砍尾巴幻方.构造8阶最完美幻方的过程如图4-7，图4-8和图4-9所示.图4-78阶基方阵A图4-8行变换后所得方阵B图4-98阶最完美幻方图4-9是一个正规的8阶最完美幻方，其每一行，每一列上的8个数字之和都等于260，对角线或泛对角......
2023-10-20
-
构造4阶最完美的砍尾巴幻方详细阅读
按构造双偶数阶最完美幻方的三步法先构造一个4阶最完美幻方，再仿照同一个三步法构造一个由尾数组成的最完美幻方，两个幻方对应的元素结合所得就是一个4阶最完美的砍尾巴幻方.构造4阶最完美幻方的过程如图4-1，图4-2和图4-3所示.图4-14阶基方阵A图4-2行变换后所得方阵B图4-34阶最完美幻方图4-3是一个正规的4阶最完美幻方，其每一行，每一列上的4个数字之和都等于34，对角线或泛对角线上的......
2023-10-20
- 详细阅读
-
构造一个8阶最完美的掐头去尾幻方详细阅读
第一步，构造一个8阶最完美幻方的过程如图6-1，图6-2和图6-3所示.图6-18阶基方阵A图6-2行变换后所得方阵图6-38阶最完美幻方上述8阶最完美幻方其所有数都加10，得一个新的由11～74的自然数组成的非正规的8阶最完美幻方B，如图6-4所示.图6-4非正规的8阶最完美幻方B第二步，从1～9的自然数中任意选定其和相等的四对数，比如7与4，2与9，5与6，8与3作为尾数，它们的和都是......
2023-10-20
相关推荐