第一步，安装4阶基方阵A.把1～16按从小到大均分为4组.注意到1～4的自然数列中处于“中心”对称位置上的两个自然数，其和都等于4+1=5，我们共有2对这样的自然数1，4和2，3，在每对自然数中随意选取一个自然数，将这2个自然数随意排序，余下的2个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于4+1=5.比如我们取2，4，1，3这样的顺序，相应的自然数5～8重新按2+4=6，4+......
2023-10-20
阶最完美幻方->幻中之幻：8阶完美幻方
【摘要】：第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.注意到1～8的自然数列中处于“中心”对称位置上的两个自然数，其和都等于8+1=9，我们共有4对这样的自然数1，8；2，7；3，6和4，5，在每对自然数中随意选取一个自然数，将这4个自然数随意排序，余下的4个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于8+1=9.比如我们取7，3，4，8，1，5，6，2这样的顺序，相应的自
第一步，安装8阶基方阵A.
把1～64按从小到大均分为8组.注意到1～8的自然数列中处于“中心”对称位置上的两个自然数，其和都等于8+1=9，我们共有4对这样的自然数1，8；2，7；3，6和4，5，在每对自然数中随意选取一个自然数，将这4个自然数随意排序，余下的4个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于8+1=9.比如我们取7，3，4，8，1，5，6，2这样的顺序，相应的自然数9～16重新按7+8=15，3+8=11，4+8=12，8+8=16，1+8=9，5+8=13，6+8=14，2+8=10排序；自然数17～24重新按7+2·8=23，3+2·8=19，4+2·8=20，8+2·8=24，1+2·8=17，5+2·8=21，6+2·8=22，2+2·8=18排序；自然数25～32重新按31，27，28，32，25，29，30，26排序；自然数33～40重新按39，35，36，40，33，37，38，34排序；自然数41～48重新按47，43，44，48，41，45，46，42排序；自然数49～56重新按55，51，52，56，49，53，54，50排序；自然数57～64重新按63，59，60，64，57，61，62，58排序.
与构造最简单的8阶最完美幻方三步法的第一步相同，第1列自上而下按7，3，4，8，1，5，6，2的顺序安装1～8的自然数，第2列自下而上按15，11，12，16，9，13，14，10的顺序安装自然数9～16，第3列自上而下按23，19，20，24，17，21，22，18的顺序安装自然数17～24，第4列自下而上按31，27，28，32，25，29，30，26的顺序安装自然数25～32；
第8列自下而上按39，35，36，40，33，37，38，34的顺序安装自然数33～40，第7列自上而下按47，43，44，48，41，45，46，42的顺序安装自然数41～48，第6列自下而上按55，51，52，56，49，53，54，50的顺序安装自然数49～56，第5列自上而下按63，59，60，64，57，61，62，58的顺序安装自然数57～64.所得到的8阶方阵叫作基方阵A，基方阵A的每一行数字之和都等于幻方常数260.如图1-12所示.
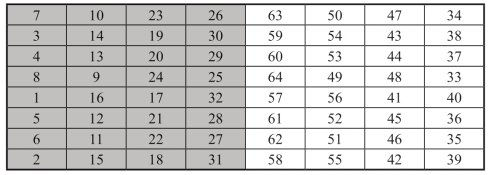
图1-12 8阶基方阵A
第二步，对基方阵A做行变换，基方阵A上半部分不变，第5，6，7，8行依次作为新方阵的第8，7，6，5行，所得方阵记为B.如图1-13所示.
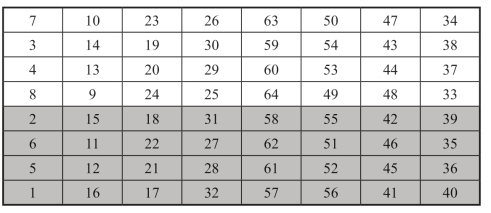
图1-13 行变换后所得方阵B
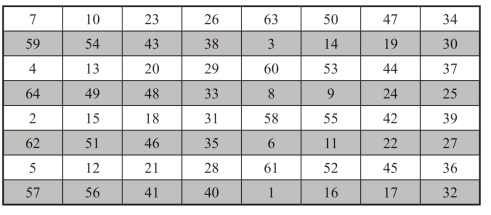
第三步，方阵B偶数行左右两部分交换所得方阵记为C，所得的8阶方阵C就是一个8阶最完美幻方.如图1-14所示.
(www.chuimin.cn)
图1-14 8阶最完美幻方
方阵C每一行，每一列上的8个数字之和都等于260，对角线或泛对角线上8个数之和亦都等于260，对角线或泛对角线上，间距为4个位置的2个数字之和都等于82+1=65；任意位置上截取一个2×2的小方阵，其中4数之和都等于2（82+1）=130，所以方阵C是一个8阶最完美幻方.
用三步法可构造出24（4·3·2·1）=384个不同的8阶最完美幻方.不包括每一个8阶最完美幻方可以衍生出的82=64个（包括这个8阶最完美幻方）8阶最完美幻方.
注意到每一个由三步法得到的8阶最完美幻方，如图1-14，其左半部分4列中，任意选取若干列各自与与其相距4列的相应列做列交换，所得仍是一个8阶最完美幻方.即得出24－1=15个不同的8阶最完美幻方（包括这个8阶最完美幻方）.作为一个例子，如图1-15所示.
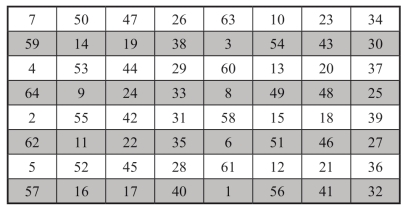
图1-15 对应列交换后所得8阶最完美幻方
又注意到每一个由三步法得到的8阶最完美幻方，如图1-14，其左半部分4列在左半部分中向右顺移，右半部分亦做相应的右移，所得仍是一个8阶最完美幻方.即得出4个不同的8阶最完美幻方（包括这个8阶最完美幻方）.作为一个例子，如图1-16所示.
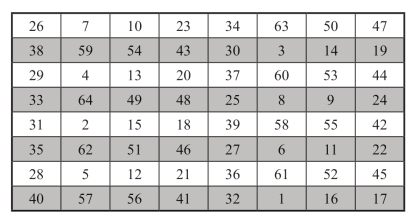
图1-16 左右两部分相应右移后所得8阶最完美幻方
所以由三步法实际上可构造出24（4·3·2·1）（24-1）·4=23040个不同的8阶最完美幻方.
有关幻中之幻的文章
- 详细阅读
- 详细阅读
-
最完美的8阶最简单幻方—幻中之幻详细阅读
第一步，安装8阶基方阵A.把1～64按从小到大均分为8组.第1列按自上而下的顺序安装自然数1～8，第2列按自下而上的顺序安装自然数9～16，第3列按自上而下的顺序安装自然数17～24，第4列按自下而上的顺序安装自然数25～32；第8列按自下而上的顺序安装自然数33～40，第7列按自上而下的顺序安装自然数41～48，第6列按自下而上的顺序安装自然数49～56，第5列按自上而下的顺序安装自然数57～6......
2023-10-20
-
12阶最完美幻方-幻中之幻详细阅读
第一步，安装12阶基方阵A.把1～144按从小到大均分为12组.注意到1～12的自然数列中处于“中心”对称位置上的两个自然数，其和都等于12+1=13，我们共有6对这样的自然数1，12；2，11；3，10；4，9；5，8和6，7，在每对自然数中随意选取一个自然数，将这6个自然数随意排序，余下的6个自然数的排序必须使处于“中心”对称位置上的两个自然数，其和都等于12+1=13.比如我们取5，7，10......
2023-10-20
-
构造5阶易位完美幻方：幻中之幻详细阅读
从1～9的自然数中任意选定5个数，比如1，3，6，5，8，它们的和是23.任意选定另外5个数，使它们的和亦是23，比如9，2，7，1，4.1，3，6，5，8，各取5次，仿照构造完美幻方的两步法[1]，得到一个不连续数的五阶完美幻方，其幻方常数为是23.其基方阵如图2-12所示，所得不连续数的5阶完美幻方，如图2-13所示.图2-125阶基方阵图2-13不连续数的5阶完美幻方9，2，7，1，4.......
2023-10-20
-
构造12阶最完美砍尾幻方，惊叹幻中之幻！详细阅读
按构造双偶数阶最完美幻方的三步法先构造一个12阶最完美幻方，再仿照同一个三步法构造一个由尾数组成的12阶最完美幻方，两个幻方对应的元素结合所得就是一个12阶最完美的砍尾巴幻方.构造12阶最完美幻方的过程如图4-13，图4-14和图4-15所示.图4-1312阶基方阵A图4-14行变换后所得方阵B图4-1512阶最完美幻方图4-15是一个正规的12阶最完美幻方，其每一行，每一列上的12个数字之......
2023-10-20
-
构造完美7阶幻方-幻中之幻详细阅读
第一步，由构造对称完美幻方的两步法[1]得到的一个7阶对称完美幻方，其幻方常数是175.中心对称位置上两个元素之和都等于50.其基方阵A如图5-9所示，7阶对称完美幻方如图5-10所示.图5-97阶基方阵A图5-107阶对称完美幻方上述7阶对称完美幻方其所有数都加10，得一个新的由11～59的自然数组成的非正规的7阶对称完美幻方B，如图5-11所示.图5-11非正规的7阶对称完美幻方B第二步......
2023-10-20
-
阶完美或对称完美的砍尾巴幻方：幻中之幻详细阅读
）2=2=518400个不同的7阶幻方，7阶完美幻方.48·8=384个不同的7阶对称完美幻方.显然由两步法得到的7阶砍尾巴幻方、7阶完美的砍尾巴幻方，7阶对称完美的砍尾巴幻方比原先得到的幻方，完美幻方，对称完美幻方多得多.......
2023-10-20
相关推荐