周期为2π的周期函数的傅里叶级数-高等数学

2023-10-19 理论教育版权反馈

【摘要】：叫作函数f的傅里叶系数.傅里叶级数：三角级数称为傅里叶级数，其中a0，a1，b1，…是傅里叶系数.问题一个定义在内的周期为2π的函数f，如果它在一个周期上可积，则一定可以作出f的傅里叶级数.然而，函数f的傅里叶级数是否一定收敛？

我们称函数系

为三角函数系.容易验证，三角函数系有下面的重要性质：如果m，n是正整数，则

三角函数系的这个性质称为三角函数系的正交性.

三角函数系中任何两个相同的函数的乘积在区间[-π，π]上的积分不等于零，即

问题设f（x）是周期为2π的周期函数，且能展开成三角级数：

那么系数a0，a1，b1，…与函数f（x）之间存在着怎样的关系？

假定三角级数可逐项积分，则

类似地，.

傅里叶系数：

系数a0，a1，b1，…叫作函数f（x）的傅里叶系数.

傅里叶级数：三角级数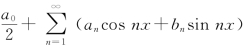 pagenumber_ebook=132,pagenumber_book=126 称为傅里叶级数，其中a0，a1，b1，…是傅里叶系数.

问题一个定义在（-∞，+∞）内的周期为2π的函数f（x），如果它在一个周期上可积，则一定可以作出f（x）的傅里叶级数.然而，函数f（x）的傅里叶级数是否一定收敛？如果它收敛，它是否一定收敛于函数f（x）？一般来说，这两个问题的答案都不是肯定的.

定理（收敛定理，狄利克雷充分条件）设f（x）是周期为2π的周期函数，如果它满足：在一个周期内连续或只有有限个第一类间断点，在一个周期内至多只有有限个极值点，则f（x）的傅里叶级数收敛，并且

当x是f（x）的连续点时，级数收敛于f（x）；

当x是f（x）的间断点时，级数收敛于.

例1 设f（x）是周期为2π的周期函数，它在[-π，π）内的表达式为

将f（x）展开成傅里叶级数.

解所给函数满足收敛定理的条件，它在点x=kπ（k=0，±1，±2，…）处不连续，在其他点处连续，从而由收敛定理知道f（x）的傅里叶级数收敛，并且当x=kπ时级数收敛于

当x≠k时级数收敛于f（x）.(www.chuimin.cn)

傅里叶系数计算如下：

于是f（x）的傅里叶级数展开式为

周期延拓：设f（x）只在[-π，π]上有定义，我们可以在[-π，π）或（-π，π]外补充函数f（x）的定义，使它拓广成周期为2π的周期函数F（x），在（-π，π）内，

例2 将函数

展开成傅里叶级数.

解所给函数在区间[-π，π]上满足收敛定理的条件，并且拓广为周期函数时，它在每一点x处都连续，因此拓广的周期函数的傅里叶级数在[-π，π]上收敛于f（x）.

傅里叶系数为

于是f（x）的傅里叶级数展开式为

正弦级数和余弦级数：

当f（x）为奇函数时，f（x）cos nx是奇函数，f（x）sin nx是偶函数，故傅里叶系数为

因此奇函数的傅里叶级数是只含有正弦项的正弦级数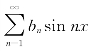 pagenumber_ebook=133,pagenumber_book=127 .

当f（x）为偶函数时，f（x）cos nx是偶函数，f（x）sin nx是奇函数，故傅里叶系数为

因此偶函数的傅里叶级数是只含有余弦项的余弦级数.

例3 设f（x）是周期为2π的周期函数，它在[-π，π）内的表达式为f（x）=x.将f（x）展开成傅里叶级数.

解首先，所给函数满足收敛定理的条件，它在点x=（2k+1）π（k=0，±1，±2，…）不连续，因此f（x）的傅里叶级数在函数的连续点x≠（2k+1）π收敛于f（x），在点x=（2k+1）π（k=0，±1，±2，…）收敛于

其次，若不计x=（2k+1）π（k=0，±1，±2，…），则f（x）是周期为2π的奇函数.于是

an=0（n=0，1，2，…），而

f（x）的傅里叶级数展开式为