泰勒级数：收敛条件与展开条件

2023-10-19 理论教育版权反馈

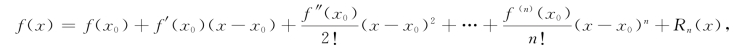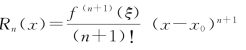【摘要】：泰勒多项式：如果f（x）在点x0的某邻域内具有各阶导数，则在该邻域内f（x）近似等于其中（ξ介于x与x0之间）.如果f（x）存在任意阶导数，且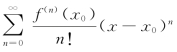的收敛半径为R，则于是成立的充分必要条件是：当|x-x0|＜R时，，即下面定理成立.定理设函数f（x）在点x0的某一邻域U（x0）内具有各阶导数，则f（x）在该邻域内能展开成泰勒级数的充分必要条件是f（x）的泰勒公式中余项Rn（x）当n→∞时极限为零，即麦

泰勒多项式：如果f（x）在点x0的某邻域内具有各阶导数，则在该邻域内f（x）近似等于 pagenumber_ebook=127,pagenumber_book=121 其中（ξ介于x与x0之间）.

如果f（x）存在任意阶导数，且 pagenumber_ebook=127,pagenumber_book=121 的收敛半径为R，则

于是

成立的充分必要条件是：当|x-x0|＜R时，，即下面定理成立.

定理设函数f（x）在点x0的某一邻域U（x0）内具有各阶导数，则f（x）在该邻域内能展开成泰勒级数的充分必要条件是f（x）的泰勒公式中余项Rn（x）当n→∞时极限为零，即

麦克劳林级数在泰勒级数中取x0=0，得

此级数称为f（x）的麦克劳林级数.(www.chuimin.cn)

展开式的唯一性：如果f（x）能展开成x的幂级数，则这种展开式是唯一的，它一定与f（x）的麦克劳林级数一致.

这是因为，如果f（x）在点x0=0的某邻域（-R，R）内能展开成x的幂级数，即

对一切x∈（-R，R）成立，根据幂级数在收敛区间内可以逐项求导，有

把x=0代入以上各式，得

应注意的问题：如果f（x）能展开成x的幂级数，那么这个幂级数就是f（x）的麦克劳林级数.但是，反过来，如果f（x）的麦克劳林级数在点x0=0的某邻域内收敛，它却不一定收敛于f（x）.因此，如果f（x）在x0=0处具有各阶导数，则f（x）的麦克劳林级数虽能作出来，但这个级数是否能在某个区间内收敛，以及是否收敛于f（x）却需要进一步考查.

泰勒级数：收敛条件与展开条件

相关推荐