幂级数收敛性及形式-高等数学

2025-09-30 理论教育版权反馈

【摘要】：函数项级数中简单而常见的一类级数就是各项都是幂函数的函数项级数，这种形式的级数称为幂级数，它的形式是其中常数a0，a1，a2，…叫作幂级数的系数.例如：，.注幂级数的一般形式是经变换t=x-x0就得.对于给定的幂级数，它的收敛域是怎样的呢？

函数项级数中简单而常见的一类级数就是各项都是幂函数的函数项级数，这种形式的级数称为幂级数，它的形式是

其中常数a0，a1，a2，…，an，…叫作幂级数的系数.

例如： pagenumber_ebook=123,pagenumber_book=117 ，

注幂级数的一般形式是

经变换t=x-x0就得.

对于给定的幂级数，它的收敛域是怎样的呢？

显然，当x=0时，幂级数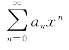 pagenumber_ebook=123,pagenumber_book=117 收敛于a0，这说明幂级数的收敛域总是非空的.再来考查幂级数

的收敛性.这个级数是等比级数，可以看成公比为x的几何级数.当|x|＜1时，它是收敛的；当|x|≥1时，它是发散的.因此它的收敛域为（-1，1），在收敛域内有

定理1（阿贝尔定理）如果级数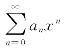 pagenumber_ebook=123,pagenumber_book=117 当x=x0（x0≠0）时收敛，则满足不等式|x|＜|x0|的一切x使该幂级数绝对收敛.反之，如果级数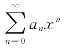当x=x0时发散，则满足不等式|x|＞|x0|的一切x使该幂级数发散.

简要证明设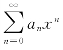 pagenumber_ebook=123,pagenumber_book=117 在点x0收敛，则有，于是数列有界，于是存在一个常数M，使得.因为

而当|x|＜|x0|时，等比级数 pagenumber_ebook=123,pagenumber_book=117 收敛，所以级数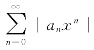收敛，也就是级数绝对收敛.

定理的第二部分可用反证法证明.

推论如果幂级数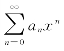 pagenumber_ebook=123,pagenumber_book=117 不是仅在点x=0一点处收敛，也不是在整个数轴上都收敛，则必有一个完全确定的正数R存在，使得

（1）当|x|＜R时，幂级数绝对收敛；

（2）当|x|＞R时，幂级数发散；

（3）当x=R与x=-R时，幂级数可能收敛也可能发散.(https://www.chuimin.cn)

正数R通常叫作幂级数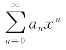 pagenumber_ebook=124,pagenumber_book=118 的收敛半径.开区间（-R，R）叫作幂级数的收敛区间.再由幂级数在x=±R处的收敛性就可以决定它的收敛域.幂级数的收敛域是（-R，R），[-R，R），（-R，R]，[-R，R]之一.

规定：若幂级数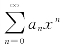 pagenumber_ebook=124,pagenumber_book=118 只在x=0收敛，则规定收敛半径R=0；若幂级数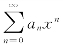对一切x都收敛，则规定收敛半径R=+∞，这时收敛域为（-∞，+∞）.

定理2 设幂级数 pagenumber_ebook=124,pagenumber_book=118 的所有系数an≠0，如果，其中an，an+1是幂级数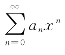相邻两项的系数，则该幂级数的收敛半径

求幂级数 pagenumber_ebook=124,pagenumber_book=118 收敛域的基本步骤：

（1）求出收敛半径R；

（2）判别常数项级数的收敛性；

（3）写出幂级数的收敛域.

例1 求幂级数

的收敛半径与收敛域.

解因为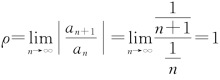 pagenumber_ebook=124,pagenumber_book=118 ，所以收敛半径为.

当x=1时，幂级数成为，是收敛的；

当x=-1时，幂级数成为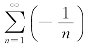 pagenumber_ebook=124,pagenumber_book=118 ，是发散的.因此，收敛域为（-1，1].

例2 求幂级数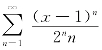 pagenumber_ebook=124,pagenumber_book=118 的收敛域.

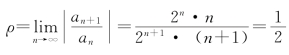解令t=x-1，上述级数变为.因为 pagenumber_ebook=124,pagenumber_book=118 ，所以收敛半径R=2.

当t=2时，级数成为 pagenumber_ebook=125,pagenumber_book=119 ，此级数发散；当t=-2时，级数成为，此级数收敛.因此级数的收敛域为-2≤t＜2，即-2≤x-1＜2，可得-1≤x＜3，所以原级数的收敛域为[-1，3）.