首页理论教育高等数学：正项级数及审敛法

高等数学：正项级数及审敛法

2025-09-30 理论教育版权反馈

【摘要】：各项都是正数或零的级数称为正项级数.易知正项级数的部分和数列{sn}是单调增加数列，即s1≤s2≤…

各项都是正数或零的级数称为正项级数.易知正项级数 pagenumber_ebook=118,pagenumber_book=112 的部分和数列{sn}是单调增加数列，即s1≤s2≤…≤sn≤…，根据数列的单调有界准则知，{sn}收敛的充分必要条件是{sn}有界.因此得到下述重要定理.

定理1 正项级数收敛的充分必要条件是它的部分和数列{sn}有界.

上述定理的重要性主要并不在于利用它来直接判别正项级数的收敛性，而在于它是证明下面一系列判别法的基础.

定理2（比较审敛法）设和都是正项级数，且un≤vn（k＞0，∀n≥N）.

（1）若收敛，则收敛；（2）若发散，则发散.

例1 证明级数 pagenumber_ebook=119,pagenumber_book=113 是发散的.

证明因为 pagenumber_ebook=119,pagenumber_book=113 ，而级数是发散的，根据比较审敛法可知所给级数也是发散的.

p-级数 pagenumber_ebook=119,pagenumber_book=113 ，其中常数p＞0.

其收敛性：当p＞1时收敛，当p≤1时发散.

定理3（比较审敛法的极限形式）设都是正项级数，

（1）当时，这两个级数有相同的敛散性；

（2）当时，若级数收敛，则级数收敛；

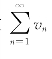（3）当时，若级数 pagenumber_ebook=119,pagenumber_book=113 发散，则级数发散.

例2 判别级数的敛散性.(https://www.chuimin.cn)

解因为 pagenumber_ebook=119,pagenumber_book=113 ，而级数发散，根据比较审敛法的极限形式，级数发散.

例3 判别级数 pagenumber_ebook=119,pagenumber_book=113 的敛散性.

解因为 pagenumber_ebook=119,pagenumber_book=113 ，而级数收敛，根据比较审敛法的极限形式，级数收敛.

定理4（比值审敛法，达朗贝尔判别法）若正项级数的后项与前项之比的极限等于ρ，即

则当ρ＜1时级数收敛；当 pagenumber_ebook=119,pagenumber_book=113 时级数发散；当ρ=1时级数可能收敛也可能发散，本判别法失效.

例4 判别级数的敛散性.

证明，比值审敛法失效.因为

而级数 pagenumber_ebook=120,pagenumber_book=114 收敛，所以由比较审敛法可知所给级数收敛.

定理5（根值审敛法，柯西判别法）设是正项级数，如果它的一般项un的n次根的极限等于ρ，即

则当ρ＜1时级数收敛；当ρ＞1（或时级数发散；当ρ=1时级数可能收敛也可能发散.

例5 证明级数是收敛的.

证明因，故根据根值审敛法，所给级数收敛.