首页理论教育常数项级数的概念与规定

常数项级数的概念与规定

2025-09-30 理论教育版权反馈

【摘要】：我们学习初等数学已经知道：有限个实数相加，其结果是一个实数.那么，“无限个实数相加”会出现什么样的结果呢？叫作（常数项）无穷级数，简称级数，记为，即式中的每一个数称为常数项级数的项，其中第n项un叫作级数的一般项或通项.提出问题：有限个数相加得到的是一个确定的和数，而无限个数相加得到的是什么？这需要从极限的观点给出规定.级数的前n项和称为级数的部分和.当n依次取1，2，3，…

我们学习初等数学已经知道：有限个实数相加，其结果是一个实数.那么，“无限个实数相加”会出现什么样的结果呢？在第一章我们提到《庄子·天下篇》“一尺之棰，日取其半，万世不竭”，即：.

这就是“无限个实数相加”的实例，我们知道它的和是1.还有如下“无限个实数相加”的表达式

可写作

也可写作

由此提出，“无限个实数相加”是否存在和？如果存在，和等于什么？无限个数相加，不能用有限个数相加的概念，必须建立新的理论.

一般地，给定一个数列u1，u2，u3，…，un，…，则由该数列构成的表达式u1+u2+u3+…+un+…叫作（常数项）无穷级数，简称级数，记为 pagenumber_ebook=115,pagenumber_book=109 ，即

式中的每一个数称为常数项级数的项，其中第n项un叫作级数的一般项或通项.

提出问题：有限个数相加得到的是一个确定的和数，而无限个数相加得到的是什么？怎样才算得到一个确定的和数？这需要从极限的观点给出规定.

级数的前n项和

称为级数的部分和.当n依次取1，2，3，…时，它们构成一个新的数列{sn}称为部分和数列.根据数列{sn}是否存在极限，我们引进级数（11.1.1）的收敛与发散的概念.

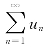定义如果级数的部分和数列{sn}有极限s，即，则称无穷级数 pagenumber_ebook=116,pagenumber_book=110 收敛，这时极限s叫作级数的和，并写成

如果{sn}没有极限，则称无穷级数发散.

当级数收敛时，其部分和sn是级数的和s的近似值，它们之间的差值

叫作级数 pagenumber_ebook=116,pagenumber_book=110 的余项.

例1 讨论等比级数（几何级数）(https://www.chuimin.cn)

的敛散性，其中a≠0，q叫作级数的公比.

解如果q≠1，则部分和

当|q|＜1时，因为，所以此时级数收敛，其和为.

当|q|＞1时，因为，所以此时级数发散.

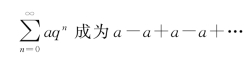如果|q|=1，则当q=1时，，因此级数发散；当q=-1时，级数 pagenumber_ebook=116,pagenumber_book=110 ，因为sn随着n为奇数或偶数而等于a或零，所以sn的极限不存在，从而这时级数也发散.

综上所述，级数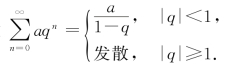 pagenumber_ebook=116,pagenumber_book=110

例2 证明级数

是发散的.

证明此级数的部分和为显然，，因此所给级数是发散的.

例3 判别无穷级数

的收敛性.

解由，得

所以，即该级数收敛，其和为1.