首页理论教育高数二第2版总习题十，曲线和曲面积分计算与化简

高数二第2版总习题十，曲线和曲面积分计算与化简

2023-10-19 理论教育版权反馈

【摘要】：1.填空.（1）第二类曲线积分化成第一类曲线积分是________，其中α、β、γ为有向曲线弧Γ上点（x，y，z）处的_________的方向角；（2）第二类曲面积分化成第一类曲面积分是_________，其中α、β、γ为有向曲面Σ上点（x，y，z）处_________的方向角.2.计算下列曲线积分：（1），其中L为由y=x及y=x2所围成区域的边界；（2），其中L为摆线x=a（t-sin t），

1.填空.

（1）第二类曲线积分化成第一类曲线积分是________，其中α、β、γ为有向曲线弧Γ上点（x，y，z）处的_________的方向角；

（2）第二类曲面积分 pagenumber_ebook=113,pagenumber_book=107 化成第一类曲面积分是_________，其中α、β、γ为有向曲面Σ上点（x，y，z）处_________的方向角.

2.计算下列曲线积分：

（1），其中L为由y=x及y=x2所围成区域的边界；

（2），其中L为摆线x=a（t-sin t），y=a（1-cos t）上对应t从0到2π的一段弧；

（3），其中Γ是曲线x=t，y=t2，z=t3上由t1=0到t2=1的一段弧；

（4），其中L为上半圆周（x-a）2+y2=a2，y≥0，沿逆时针方向；

（5），其中L为过（0，0），（0，1），（1，2）的圆周.

3.在过点O（0，0）与A（π，0）的曲线族y=a sin x（a＞0）中，求一条曲线L，使沿该曲线从点O到点A的积分值最小.

4.计算 pagenumber_ebook=113,pagenumber_book=107 ，其中L为

（1）不包围且不通过原点的任意曲线；(www.chuimin.cn)

（2）以原点为中心、ε为半径的圆周，取顺时针方向；

（3）包围原点的任意闭曲线（无重点），取正向.

5.证明曲线积分在整个x Oy面内与路径无关并计算积分值.

6.计算下列曲面积分：

（1）在第一卦限部分；

(2);

（3），其中Σ为锥面（0≤z≤h）的外侧；

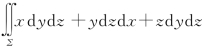（4） pagenumber_ebook=114,pagenumber_book=108 ，其中Σ为半球面的上侧；

（5），其中Σ为球面x2+y2+z2+1（x≥0，y≥0）的外侧.

7.求均匀曲面的重心坐标.