Σ为闭区域时，曲面积分与二重积分的关系

2023-10-19 理论教育版权反馈

【摘要】：1.当Σ为x Oy面内的一个闭区域时，曲面积分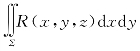与二重积分有什么关系？

1.当Σ为x Oy面内的一个闭区域时，曲面积分 pagenumber_ebook=111,pagenumber_book=105 与二重积分有什么关系？

2.计算下列对坐标的曲面积分：

（1），其中Σ是球面x2+y2+z2=R2下半部分的下侧；

（2），其中Σ是柱面x2+y2=1被平面z=0及z=3所截得的在第一卦限内部分的前侧；

（3） pagenumber_ebook=111,pagenumber_book=105 ，其中f（x，y，z）为连续函数，Σ是平面x-y+z=1在第四卦限部分的上侧；

（4），其中Σ是平面x=0，y=0，z=0，x+y+z=1所围成的空间区域整个边界曲面的外侧.

阅读与拓展

微积分学的应用

鹦鹉螺的对数螺线是微积分增长变幻的经典图像.(www.chuimin.cn)

微积分学的发展与应用几乎影响了现代生活的所有领域.它与大部分科学分支关系密切，包括精算、计算机、统计、工程、商业、医药、人口统计，特别是物理学；经济学亦经常会用到微积分学.几乎所有现代技术，如建筑、航空等都以微积分学作为基本数学工具.微积分使数学可以在变量和常量之间互相转化，让我们可以在已知一种方式时推导出另一种方式.

物理学大量应用微积分，所有经典力学和电磁学都与微积分有密切联系.已知密度的物体质量、动摩擦力、保守力场的总能量都可用微积分来计算.例如，将微积分应用到牛顿第二定律中：一般将导数称为变化率.物体动量的变化率等于向物体同一方向所施的力.今天常用的表达方式是F=ma，它包含了微分，因为加速度是速度的导数，或是位置矢量的二阶导数.已知物体的加速度，就可以得出它的路径.

麦克斯韦尔的电磁学和爱因斯坦的广义相对论都应用了微积分.化学使用微积分来计算反应速率，放射性衰退.生物学用微积分来计算种群动态，用输入繁殖和死亡率来模拟种群改变.

微积分可以与其他数学分支交叉混合.例如，用混合线性代数来求得值域中一组数列的“最佳”线性近似.它也可以用在概率论中来确定由假设密度方程产生的连续随机变量的概率.在解析几何对方程图像的研究中，微积分可以求得最大值、最小值、斜率、凹度、拐点等.

格林公式连接了一个封闭曲线上的线积分与一个边界为C且平面区域为D的双重积分.它被设计为求积仪工具，用以量度不规则的平面面积.例如，它可以在设计时计算不规则的花瓣床、游泳池的面积.

在医疗领域，微积分可以计算血管最优支角，将血流最大化.通过药物在体内的衰退数据，微积分可以推导出服用量.在核医学中，它可以为治疗肿瘤建立放射输送模型.

在经济学中，微积分可以通过计算边际成本和边际利润来确定最大收益.

微积分也被用于寻找方程的近似值.实践中，它用于解微分方程，计算相关的应用题，如牛顿法、定点循环、线性近似等.比如，宇宙飞船利用欧拉方法来求得零重力环境下的近似曲线.

Σ为闭区域时，曲面积分与二重积分的关系

相关推荐