隐函数存在定理1 设函数F（x，y）在点P（x0，y0）的某一邻域内具有连续的偏导数，且F（x0，y0）=0，Fy（x0，y0）≠0，则方程F（x，y）=0在点（x0，y0）的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数y=f（x），它满足条件y0=f（x0），并有式（8.5.2）就是隐函数的求导公式.这个定理我们不证.现仅就式（8.5.2）作如下推导.将方程（8.5.1）所确定的函数y......
2023-10-19
隐函数存在定理推广到方程组的情形
【摘要】：下面将隐函数存在定理推广到方程组的情形.例如，考虑方程组这时，在四个变量中，一般只能有两个变量独立变化，因此方程组（8.5.4）就有可能确定两个二元函数.可以由函数F、G的性质来断定由方程组（8.5.4）所确定的两个二元函数的存在性以及它们的性质.我们有下面的定理.隐函数存在定理3 设F（x，y，u，v）、G（x，y，u，v）在点P（x0，y0，u0，v0）的某一邻域内具有对各个变量的连续偏导数，
下面将隐函数存在定理推广到方程组的情形.例如，考虑方程组
这时，在四个变量中，一般只能有两个变量独立变化，因此方程组（8.5.4）就有可能确定两个二元函数.可以由函数F、G的性质来断定由方程组（8.5.4）所确定的两个二元函数的存在性以及它们的性质.我们有下面的定理.
隐函数存在定理3 设F（x，y，u，v）、G（x，y，u，v）在点P（x0，y0，u0，v0）的某一邻域内具有对各个变量的连续偏导数，又F（x0，y0，u0，v0）=0，G（x0，y0，u0，v0）=0，且偏导数所组成的函数行列式（或称雅可比（Jacobi）式）：
在点P（x0，y0，u0，v0）不等于零，则方程F（x，y，u，v）=0，G（x，y，u，v）=0，在点P（x0，y0，u0，v0）的某一邻域内恒能唯一确定一组单值连续且具有连续导数的函数u=u（x，y），v=v（x，y），并有
式（8.5.5）～式（8.5.8）推导与前面类似.下面通过例子介绍公式的应用.(www.chuimin.cn)
例3 设xu-yv=0，y u+xv=1，求
.
解 将所给方程的两边对x求导并移项，得
在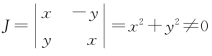
的条件下，
将所给方程的两边对y求导，用同样的方法在J=x2+y2≠0的条件下可得
有关高等数学（二）（第2版）的文章
- 详细阅读
-
拉氏变换定理存在-复变函数及其应用详细阅读
可以看出,拉式变换存在的条件要比傅氏变换存在的条件弱得多,但是对一个函数作拉氏变换也要具备一定的条件.对f提什么要求才能使f与指数衰减函数e-αt 的乘积在无穷区间上绝对可积？实数α=Re=Re应该取多大呢？......
2023-10-30
-
复合函数、反函数及隐函数导数计算详细阅读
【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式：（1）C′=0（C是常数），（2）（xμ）′=μxμ-1，（3）（ax）′=axlna（常数a>0但a≠1），特别地，（ex）′=ex，（4），特别地，，（5）（sinx）′=cosx， （6）（cosx）′=-sinx，（7）（tanx）′=sec2x， （8）（cotx）′=-csc2x，（9）（secx）′=secx......
2023-10-27
-
泰勒定理|复变函数应用详细阅读
对于一元实函数来说,若f(x)在点x0的某邻域内有任意阶的导数,并且在该邻域内恒有余项则f(x)在点x0的该邻域内的泰勒(Taylor)级数展开式为复变函数中,函数f(x)在点z0的某邻域内有任意阶导数等价于它在该邻域内解析,对于解析函数有下面的展开定理.定理1(泰勒级数展开定理) 若函数f(z) 在圆形区域D:|z-z0| ＜R内解析,则它在D内可展开为幂级数其中 若C为D内绕z0 的正向简单闭......
2023-10-30
-
复变函数的复合闭路定理详细阅读
所谓复合闭路是指一种特殊的有界多连通域D的边界曲线Γ,它由几条简单闭曲线组成,可简记为Γ=其中简单闭路C取正向; 简单闭路取负向,它们都在C 的内部且互不相交又互不包含(图3.6).上述Γ 的方向称为多连域D的边界曲线的正向.定理3(复合闭路定理) 设D是以复闭路Γ = 为边界的多连通域.若函数f(z) 在D内及其边界Γ上解析,则f(z)沿Γ的积分为零.这时有证明 只须证n = 2的情形.在区域D......
2023-10-30
-
洛朗级数展开定理、复变函数及应用详细阅读
在圆环域R1 ＜|z-z0|＜R2内处处解析的函数f(z)可以展开成z-z0的正、负幂项都有的级数,称为f(z)的洛朗(Laurent) 级数.定理1(洛朗级数展开定理) 设R1 ＜|z - z0| ＜R2 为环域D,函数f(z)在D内解析,则对D 内任意点z有其中C为在该环域内任意一条围绕点z0的正向简单闭路.证明对任意z ∈D,在D内分别作正向圆周C1 和C2,其中C1为|ζ-z0|=r1,C......
2023-10-30
-
柯西积分定理在复变函数应用中的成果详细阅读
由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式在D内恒成立.对于式右端的两个曲线积分,上述条件等式应当分别......
2023-10-30
-
高阶导数隐函数和参数方程的求导方法详细阅读
一、高阶导数在变速直线运动中，位置函数s=s对时间t的导数是速度函数v=v，而v=v对t的导数就是加速度，即加速度是位置函数的导数的导数.这种导数的导数称为s=s对时间t的二阶导数.一般地，如果函数y=f的导数仍是x的可导函数，那么y′=f′的导数，就叫作原来的函数y=f的二阶导数，记作即类似地，二阶导数的导数叫三阶导数，三阶导数的导数叫四阶导数，…......
2023-11-20
相关推荐