一、二元函数【知识点回顾】函数的定义：设有两个非空集合M、N，如果当变量x在M内任意取定一个数值时，按照确定的法则f，在N内有唯一的y与它相对应，则称y是x的函数.通常x称为自变量，变量x的取值范围M称为这个函数的定义域；y称为函数（或因变量），变量y的取值范围称为这个函数的值域.【例题1】长方形的面积S与长x（x＞0）与宽y（y＞0）的关系S=xy，当x与y变化时，都有唯一的S值和它对应.【例......
2023-11-20
高等数学第2版：二元函数连续性
【摘要】：定义3 设二元函数f（x，y）在开区域（或闭区域）D内有定义，P0（x0，y0）是D内的点（或边界点且P0∈D），如果则称函数f（x，y）在点P0（x0，y0）连续.如果函数f（x，y）在开区域（或闭区域）D内的每一点连续，那么就称函数f（x，y）在D内连续，或者称f（x，y）是D内的连续函数.若函数f（x，y）在点P0（x0，y0）处不连续，则称P0为函数f（x，y）的间断点.前面已经讨论过的函
定义3 设二元函数f（x，y）在开区域（或闭区域）D内有定义，P0（x0，y0）是D内的点（或边界点且P0∈D），如果
则称函数f（x，y）在点P0（x0，y0）连续.
如果函数f（x，y）在开区域（或闭区域）D内的每一点连续，那么就称函数f（x，y）在D内连续，或者称f（x，y）是D内的连续函数.
若函数f（x，y）在点P0（x0，y0）处不连续，则称P0为函数f（x，y）的间断点.前面已经讨论过的函数
当（x，y）→（0，0）时的极限不存在，所以点（0，0）是该函数的一个间断点.二元函数的间断点可以形成一条曲线，例如函数在圆周x2+y2=1上没有定义，所以该圆周上各点都是间断点.
与闭区域上一元连续函数的性质相类似，在有界闭区域上多元连续函数也有如下性质：
性质1（最大值和最小值定理） 在有界闭区域D上的多元连续函数一定有最大值和最小值.
性质2（介值定理） 在有界闭区域D上的多元连续函数，必可取介于最大值和最小值之间的任何值.(www.chuimin.cn)
性质3（一致连续性定理） 一切多元初等函数在其定义区域内都是连续的.
由多元初等函数的连续性可知，若点P0是函数定义区域内的一点，则点P0处的极限值等于函数在该点的函数值，即
例5 求
解 函数
是初等函数，它的定义域为
因D不是连通的，故D不是区域.但D1={（x，y）|x＞0，y＞0}是区域，且D1⊂D，所以D1是函数f（x，y）的一个定义区域.因P0（1，2）∈D1，故
例6 求
解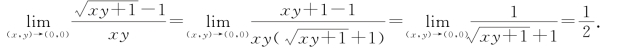
有关高等数学（二）（第2版）的文章
- 详细阅读
-
高等数学第一册：函数连续性概念详细阅读
＋a0，由于pn，故多项式函数在R内连续.又如三角函数y＝sinx，y＝cosx，由于故它们也均在R内连续.在几何上，连续函数的图形是一条连绵不断的曲线.......
2023-11-19
-
函数连续性-数学与生活详细阅读
解 由于f=1，且因此函数f在点x0=0处右连续但不左连续，所以函数f在x0=0处不连续.例4 设函数讨论f在x=1处的连续性.解 由于f=2，且因此函数f在x=1处左连续且右连续，所以函数f在x=1处连续.例5 设函数问：a为何值时，函数y=f在点x=0处连续？......
2023-11-20
-
初等函数连续性-高数上册详细阅读
）时无意义，故x＝kπ（k＝0，±1，±2，…）均为的间断点.当x＝0时，由于故x＝0为f的第一类可去型间断点；当x＝kπ（k＝±1，±2，…）为f的第二类无穷型间断点.......
2023-11-19
-
高等数学：函数单调性和凹凸性详细阅读
一、函数的单调性从图上可以直观地看出，单调增加函数的切线斜率非负（见图3-3），单调减少函数的切线斜率非正（见图3-4）.图3-3图3-4定理3.7 设函数f（x）在区间I内可导，则：1）对任意x∈I，有f′（x）＞0，则函数f（x）在I严格单调增加；2）对任意x∈I，有f′（x）＜0，则函数f（x）在I严格单调减少.证 先证1）对任意x1，x2∈I且x1＜x2，函数f（x）在区间[x1，x2]上......
2023-11-22
-
复变函数的极限与连续性详解详细阅读
复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 ＜|z - z0| ＜ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε ＞0,总存在一个实数δ ＞0(δ ＜ρ),当0 ＜|z-z0|＜δ 时,有|f(z)-A|＜ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2023-10-30
-
高等数学：函数基本性态详细阅读
初等数学中已经简单介绍了函数的有界性、单调性、奇偶性、周期性，下面分别对它们作简要概括.1）有界性定义3设函数f（x）在区间I上有定义，若存在数M1，使得当x∈I时，恒有f（x）≤M1则称函数f（x）在数集I上有上界，M1为f（x）在I上的一个上界；若存在数M2，使得当x∈I时，恒有f（x）≥M2则称函数f（x）在数集I上有下界，M2为f（x）在I上的一个下界；若f（x）在数集I上既有上界，又有......
2023-11-19
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
相关推荐