利用函数极限的定义，可得下列极限的性质.1）唯一性定理2若存在，则极限唯一.证（反证法）假设极限不唯一，则存在两个不相等的常数a，b，使得均成立.不妨设b＞a，由于取则δ1＞0，当x满足0＜｜x－x0｜＜δ1时，恒有即又由于仍取则δ2＞0，当x满足0＜｜x－x0｜＜δ2时，恒有即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，上面（1－5）、（1－6）两式均成立，但这是不可能的.......
2023-11-19
高等数学：二重极限定义及性质
【摘要】：定义2 设二元函数点f（x，y）在点P0（x0，y0）的某邻域内有定义（点P0可以除外），如果该邻域内的点P（x，y）以任意方式无限趋于点P0（x0，y0）时，对应的函数值f（x，y）无限接近于一个确定的常数A，则称常数A为函数f（x，y）当（x，y）→（x0，y0）时的极限，记作为了区别于一元函数的极限，我们把二元函数的极限叫作二重极限.必须注意，所谓二重极限存在，是指点P（x，y）以任何方式趋
定义2 设二元函数点f（x，y）在点P0（x0，y0）的某邻域内有定义（点P0可以除外），如果该邻域内的点P（x，y）以任意方式无限趋于点P0（x0，y0）时，对应的函数值f（x，y）无限接近于一个确定的常数A，则称常数A为函数f（x，y）当（x，y）→（x0，y0）时的极限，记作
为了区别于一元函数的极限，我们把二元函数的极限叫作二重极限.
必须注意，所谓二重极限存在，是指点P（x，y）以任何方式趋于点P0（x0，y0）时，函数都无限接近于A.因此，如果点P（x，y）以某一种特殊方式，例如沿着一条直线或定曲线趋于点P0（x0，y0）时，即使函数无限接近于某一确定值，我们还不能由此断定函数的极限存在.但是反过来，如果当点P（x，y）以不同方式趋于点P0（x0，y0）时，函数趋于不同的值，那么就可以断定该函数在点P0（x0，y0）处的极限不存在.下面用例子来说明这种情形.
考查函数
显然，当点P（x，y）沿x轴趋于点（0，0）时，
；又当点P（x，y）沿y轴趋于点（0，0）时，
虽然点P（x，y）以上述两种特殊方式（沿x轴或沿y轴）趋于原点时函数的极限存在并且相等，但是
并不存在.这是因为当点P（x，y）沿着直线y=kx趋于点（0，0）时，有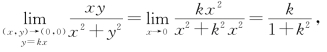
显然它是随着k值的不同而改变的.(www.chuimin.cn)
例3 求
解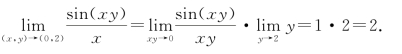
例4 求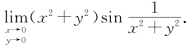
解 令u=x2+y2，则
有关高等数学（二）（第2版）的文章
- 详细阅读
-
高等数学上册：无穷大量的定义及性质详细阅读
在前面，已经多次提到“无穷大”这个概念，这里对这一变化状态给出确切的定义.我们知道，当x→□时，对应函数的绝对值｜f（x）｜无限增大，就称函数f（x）为当x→□时的无穷大量.设M为任意取定的大正数M，则不等式｜f（x）｜＞M表示函数的绝对值｜f（x）｜可以超过预先任意给定的大正数M，因此由M的任意性可知，不等式｜f（x）｜＞M表示函数的绝对值无限增大.再结合无穷大对应的极限过程的精确描述，由此得到......
2023-11-19
-
子极限的定义与性质，自变量的变化过程及其限制详细阅读
上面我们讨论了x→x0与x→∞时函数极限的定义及性质，其中自变量的变化过程x→x0是指自变量x沿x轴从x0的左、右两侧趋于x0，x→∞是指自变量x沿x轴左、右两侧离原点越来越远，趋于无穷远.但有时所讨论的极限中，其自变量的变化过程只须沿某一侧（左侧或右侧）变化，例如考察极限时，由于受函数的定义域限制，自变量在x→0的变化过程中，x只能从0的右侧趋近于0，该变化过程相当于在变化过程“x→0”中增加了......
2023-11-19
-
矩阵秩的定义及性质分析详细阅读
【主要内容】1.矩阵秩的定义设A是m×n矩阵，则称A的不为零的子行列式（简称子式）的最高阶数为A的秩，记为r（A），其中，A的k（k≤min{m，n}）阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.零矩阵的秩定义为0.2.矩阵秩的性质（1）设A是m×n矩阵，则0≤r（A）≤min{m，n}.（2）设A是m×n矩阵，k是常数，则（3）初等变换不改变矩阵的秩，即等价矩阵的秩相等.（4）设A，B......
2023-10-27
-
矩阵相似定义及性质概述详细阅读
1.矩阵相似的定义设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.2.矩阵相似的性质设A，B，C都是n阶矩阵，则有以下性质：A～A.如果A～B，则B～A.如果A～B，B～C，则A～C.如果A～B，则AT～BT，Am～Bm，λA～λB，φ～φ（其中，φ（λ）=a0+a1λ+…......
2023-10-27
-
复变指数函数的定义及性质详细阅读
从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.定义1 对任意的复数z =x+iy,定义指数函数为w =ex(cos y+i sin y),记作ez.显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez 0.当z 取实数,即y = 0......
2023-10-30
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2023-11-19
-
高等代数：实数域上的内积定义及性质详细阅读
定义6.1 在实数域R上的线性空间V中，定义一个二元函数V×V→R，称为向量α，β∈V的内积，记作<α，β>，如果下面几个条件同时成立：（1）<α，β>=<β，α>，对任意向量α，β∈V成立；（2）
2023-11-22
相关推荐