表示常量,用字母x,y,z,t,…......
2023-11-19
一般地,形如
当g(y)≠0时,方程(7.2.1)可写为
这样一来,变量y与x便被分离在等号的两端了.
设f(x)与g(x)都连续,求解方程(7.2.1),就是要寻找函数y=y(x),将它代入方程(7.2.1)后,能使此方程成为恒等式.从而,当g(y)≠0时,就有
在解微分方程时,为了突出任意常数C,常把![]() 中所含的任意常数C明确写出来.根据不定积分的第一换元法,得
中所含的任意常数C明确写出来.根据不定积分的第一换元法,得
由式(7.2.3)所确定的隐函数y=y(x)就是方程(7.2.2)的通解.事实上,由以上推导可以看出,满足方程(7.2.2)的解y=y(x)必满足方程(7.2.3);反之,对式(7.2.3)两端微分便得式(7.2.2),这说明满足式(7.2.3)的解也必满足式(7.2.2),而且,由式(7.2.3)所确定的隐函数中又含有一个任意常数,所以是通解.这种通过分离变量后对两端分别积分来求解微分方程的方法,称为分离变量法.
如果存在常数y0使g(y0)=0,那么将y=y0代入方程(7.2.1),两端均为零.这说明y=y0也是方程(7.2.1)的一个解.在许多情况下,这个解可以包含在前面所得到的通解中,即y=y0可由式(7.2.3)中让C取某特定值得到.
可分离变量的微分方程的解法:
第一步:分离变量,将方程写成g(y)d y=f(x)d x的形式;
第二步:两端积分,![]() 设积分后得G(y)=F(x)+C;
设积分后得G(y)=F(x)+C;
第三步:求出由G(y)=F(x)+C所确定的隐函数y=Φ(x)或x=Ψ(y).
G(y)=F(x)+C,y=Φ(x)或x=Ψ(y)都是方程的解,其中G(y)=F(x)+C称为隐式(通)解.(www.chuimin.cn)
例1 求微分方程![]() 的通解.
的通解.
解 此方程为可分离变量方程,分离变量后得
因为±eC1仍是任意常数,把它记作C,便得所给方程的通解为y=C ex2.
例2 铀的衰变速度与当时未衰变的铀原子的含量M成正比.已知t=0时铀的含量为M0,求在衰变过程中铀含量M(t)随时间t变化的规律.解 铀的衰变速度就是M(t)对时间t的导数![]() .由于铀的衰变速度与其含量成正比,故得微分方程
.由于铀的衰变速度与其含量成正比,故得微分方程
其中λ(λ>0)是常数,λ前的负号表示当t增加时M单调减少,即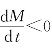 .
.
由题意,初始条件为M|t=0=M0.将方程分离变量得
即ln M=-λt+l n C,也即M=C e-λt.由初始条件,得M0=C e0=C,所以铀含量M(t)随时间t变化的规律为
例3 设降落伞从跳伞塔下落后,所受空气阻力与速度成正比,并设降落伞离开跳伞塔时速度为零.求降落伞下落速度与时间的函数关系.
解 设降落伞下落速度为v(t).降落伞所受外力为F=mg-kv(k为比例系数).根据牛顿第二运动定律F=ma,得函数v(t)应满足的方程为
初始条件为![]() .方程分离变量,得
.方程分离变量,得![]() ,
,
两端积分,得
将初始条件![]() 代入通解得
代入通解得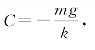 于是,降落伞下落速度与时间的函数关系为
于是,降落伞下落速度与时间的函数关系为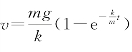 .
.
有关高等数学(二)(第2版)的文章

首先研究最简单的一阶微分方程,即可分离变量的微分方程.一、可分离变量的方程可以化成形如形式的方程称为可分离变量的微分方程.对M(x)dx=N(y)dy两端分别积分,便得方程的通解:∫M(x)dx=∫N(y)dy+C(C是任意常数).例1 求方程(1+y2)dx-x(1+x2)ydy=0的通解.解 用x(1+x2)(1+y2)除方程两边整理得两边积分因为,,所以即,或,通解为(1+x2)(1+y2)......
2023-11-22

一、建立微分方程的数学模型解:设曲线方程为y=f(x),且曲线上任意一点的坐标为(x,y).根据题意以及导数的几何意义可得两边同时求不定积分得y=∫xdx,这就是所求的曲线方程.引例2求方程y"=cosx的通解.解:一次积分得:二次积分即得到方程的通解:以上我们仅以物理学、几何学引出关于变量之间微分方程的关系,其实在化学、生物学、自动控制、电子技术等学科中都提出了许多有关微分方程的问题,从而要......
2023-11-20

考查积分的计算,其他情形以此类推.设光滑曲面Σ:z=z(x,y)与平行于z轴的直线至多交于一点,在x Oy面上的投影区域为Dxy.由对坐标的曲面积分的定义若曲面Σ取上侧,则cosγ>0,所以(ΔSi)xy=(Δσi)xy,否则(ΔSi)xy=-(Δσi)xy.又因为(ξi,ηi,ζi)是Σ上的一点,故ζi=z(ξi,ηi),从而有令λ→0取上式两端的极限,就得到式中右端符号的确定:若积分取曲面Σ上......
2023-10-19

1.填空.(1)第二类曲线积分化成第一类曲线积分是________,其中α、β、γ为有向曲线弧Γ上点(x,y,z)处的_________的方向角;(2)第二类曲面积分化成第一类曲面积分是_________,其中α、β、γ为有向曲面Σ上点(x,y,z)处_________的方向角.2.计算下列曲线积分:(1),其中L为由y=x及y=x2所围成区域的边界;(2),其中L为摆线x=a(t-sin t),......
2023-10-19

知识要点1.微分方程的基本概念:微分方程的定义、阶、通解、特解.2.可分离变量的微分方程:求解可分离变量微分方程的步骤:(1)分离变量;(2)两端分别积分,可得原方程的通解.如果问题为求特解,只需将初始条件代入求得的通解,确定常数C的值即可.3.一阶线性非齐次微分方程:形式:y′+P(x)y=Q(x).求解方法有以下两种:(1)常数变易法:第一步,先求对应的齐次微分方程y′+P(x)y=0的通解......
2023-10-26
相关推荐