密码学新进展：量子密码学与信息安全

2023-10-18 理论教育版权反馈

【摘要】：密码学把信息安全核心算法作为其研究目标，其研究内容也随着信息安全不断发展的需求而增长。这里介绍几个有代表性的密码学研究新方向，以及这些算法与传统密码算法相比较的特点。这种思想使密码算法或密码协议的安全性论证比以往的方法更加科学、可信，因此成为密码学研究的一个热点问题。（三）量子密码学量子计算是近年来兴起的一个研究领域。这是量子计算机理论的重大突破，与密码学有重要的联系。

密码学把信息安全核心算法作为其研究目标，其研究内容也随着信息安全不断发展的需求而增长。这里介绍几个有代表性的密码学研究新方向，以及这些算法与传统密码算法相比较的特点。

（一）可证明安全性

可证明安全性是指一个密码算法或密码协议，其安全性可以通过“归约”的方法得到证明。归约是把一个公认的难解问题通过多项式时间化成密码算法（或协议）的破译问题。换句话说，可证明安全性是假定攻击者能够成功，则可以从逻辑上推出这些攻击信息，可以使得攻击者或系统的使用者能够解决一个公认的数学难题。

这种思想使密码算法或密码协议的安全性论证比以往的方法更加科学、可信，因此成为密码学研究的一个热点问题。

（二）基于身份的密码技术

利用用户的部分身份信息可以直接推导出它的公开密钥的思想，早在1984年Shamir就提出来了。对普通公钥密码来说，证书权威机构是在用户生成自己的公、私密钥对之后，对用户身份和公钥进行捆绑（签名），并公开这种捆绑关系。而对于基于身份的公钥密码来说，与证书权威机构对应的可信第三方，在用户的公、私密钥对生成过程中已经参与，而且公开密钥可以选择为用户的部分身份信息的函数值。这时，用户与其公钥的捆绑关系不是通过数字签名，而是通过可信第三方对密码参数进行可信、统一（而不是单独对每个用户的公钥）、公开的保障。可以看出，在多级交叉通信的情况下，对基于身份的密码使用比普通公钥密码的使用减少了一个签名、验证层次，从而受到人们的关注。

Shamir、Fiat和Feige在1984年之后的几年中，提出了基于身份的数字签名方案和身份识别方案，但是直到2001年，Boneh和Franklin才提出一个比较完善的基于身份的加密方案。Boneh和Franklin的方案使用了椭圆曲线的Weil配对映射，从此人们总是把基于身份的密码与椭圆曲线的Weil配对联系在一起，成为近年来密码学的一个相当活跃的研究分支。

（三）量子密码学(www.chuimin.cn)

量子计算是近年来兴起的一个研究领域。早在1982年，物理学家们注意到，一些量子力学中的现象无法在现有计算机上进行仿真。但在1994年，美国电话电报公司的研究实验室提出了与现在计算机系统不同的结构模型，称为量子计算机，它通过量子力学原理实现超常规的计算。研究人员在假设可以制造一台量子计算机的前提下提出一种算法，可以在多项式时间内分解大整数。这是量子计算机理论的重大突破，与密码学有重要的联系。下面介绍的量子密钥分发技术足以显示量子密码技术的重要性。

光子和基本粒子都具有一定力学性质。力的分解与合成满足平行四边形法则或矢量的加法法则。特别地，如果有一个过0点的力F，以及一个方向e，则可以得到F在方向e上的分量F1，如图5-5所示。容易看出，F在与自身同方向上的分量是自己，而在与F垂直方向上的分量是0。

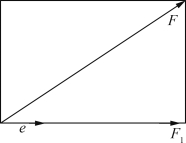
pagenumber_ebook=98,pagenumber_book=92

图5-5　力的分解

可以用另一种方法表述上述现象：用方向e对F进行测量，得到结果F1。现在用光子来做一个实验。当光子传送时，它会在某个方向（如上下、左右或某个方向）上振荡。如果一束光中的所有光子都沿着一个方向振荡，则称它是极化的，否则称为非极化的。一束光通过一个偏光镜时，将得到极化的光束。一水平方向的极化光束F，当遇到水平极化偏光镜e时，它们会全部通过，即得到的还是F。而当F遇到垂直方向的极化偏光镜e时，则没有光子能通过。一般地，一极化的光束按照其大小和极性可以看成是矢量，当遇到一个与其极性的夹角成α的偏光镜e时，则通过的光束与e同向，而且其大小为F1=F.cosα。人们发现，用偏光镜过滤光束和用方向对力进行测量，其实是同样的道理。

对一个光子的解释比上述要困难。一个光子遇到偏光镜e时，如果光子极性与一个偏光镜e是平行（或垂直）时，光子将通过（或被阻止）。但当光子极性与一个偏光镜e夹角为α时，这个光子要么改变为e的方向通过，要么被阻止，因为光子是最小单位，不能有一个不完整的光子通过。因此物理学家给出的一个稍微合理的解释是，这时这个光子改变为e的方向通过的概率为p=cosα。

密码学新进展：量子密码学与信息安全

相关推荐