(一)按防火墙软硬件形式分类如果从软硬件形式来分,防火墙可以分为软件防火墙、硬件防火墙和芯片级防火墙。之所以加上“所谓”二字,是针对芯片级防火墙来说的。目前市场上大多数防火墙都是这种所谓的硬件防火墙,它们都基于PC架构。值得注意的是,由于此类防火墙采用的依然是别人的内核,因此会受到OS本身的安全性影响。应用代理型防火墙工作在OSI的最高层,即应用层。......
2023-10-18
现行的密码算法主要包括序列密码、分组密码、公钥密码、散列函数等。现代加密技术包括对称加密、非对称加密(也称为公开密钥加密)等。
目前,加密算法是非常多的,如3DES、AES、Blowfish、IDEA、RC5、RC6、D-H、RSA、ECC、SMS4等,这些加密算法通常是公开的,也有少数几种加密算法是不公开的。对于公开的加密算法,尽管大家都知道加密方法,但对密文进行解码必须要有正确的密钥,而密钥是保密的。在保密密钥中,加密者和解密者使用相同的密钥,这种技术称为对称加密。这种加密算法的问题是,用户必须让接收人知道自己所使用的密钥,这个密钥需要双方共同保密,任何一方的失误都会导致机密的泄露,而且在告诉收件人密钥的过程中,还需要防止任何人发现或偷听密钥。而公用/私有密钥与单独的密钥不同,它使用相互关联的一对密钥,一个是公用密钥,任何人都可以知道,另一个是私有密钥,只有拥有该对密钥的人知道。如果有人发信给这个人,他就用收信人的公用密钥对信件进行加密,当发件人收到信后,他就可以用他的私有密钥进行解密,而且只有他持有的私有密钥可以解密。这种加密方式的好处显而易见。私有密钥只有一个人持有,也就更加容易进行保密,因为不需在网络上传送私人密钥,也就不用担心别人在认证会话初期截获密钥。这种技术称为非对称加密。
(一)对称密码体制
对称密钥算法加密的要求:①需要强大的加密算法。即使对手知道了算法并能访问一些或更多的密文,也不能破译密文或得出密钥。②发送方和接收方必须用安全的方式来获得保密密钥的副本,必须保证密钥的安全。如果有人发现了密钥,并知道了算法,则使用此密钥的所有通信便都是可读取的。
常规机密的安全性取决于密钥的保密性,而不是算法的保密性。也就是说,如果知道了密文和加密及解密算法的知识,解密消息也是不可能的。
对称加密算法根据其工作方式,可以分成两类。一类是一次只对明文中的一个位(有时是对一个字节)进行运算的算法,称为序列加密算法。另一类是每次对明文中的一组位进行加密的算法,称为分组加密算法。现代典型的分组加密算法的分组长度是64位。这个长度既方便使用,又足以防止分析破译。
对称加密算法的通信模型如图5-2所示。
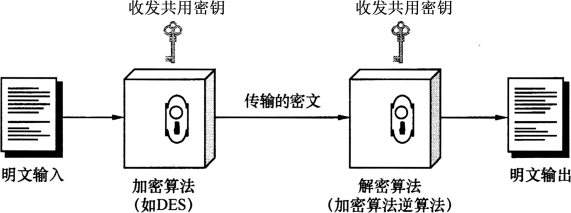
图5-2 对称加密算法的通信模型
对称密码算法的优缺点:
(1)优点:加密、解密处理速度快、保密度高等。
(2)缺点:①密钥是保证通信安全的关键,发信方必须安全、妥善地把密钥护送到收信方,不能泄露其内容,如何才能把密钥安全地送到收信方,是对称密码算法的突出问题。对称密码算法的密钥分发过程十分复杂,所花代价高。②多人通信时密钥组合的数量会出现爆炸性膨胀,使密钥分发更加复杂化,N个端用户进行两两通信,总共需要的密钥数为N(N-l)/2个。③通信双方必须统一密钥,才能发送保密的信息。如果发信者与收信人素不相识,就无法向对方发送秘密信息了。④除了密钥管理与分发问题,对称密码算法还存在数字签名困难问题(通信双方拥有同样的消息,接收方可以伪造签名,发送方也可以否认发送过某消息)。
1.DES算法
最常用的加密方案是美国国家标准和技术局(NIST)在1977年采用的数据加密标准(Data Encryption Standard,DES),它是联邦信息处理第46号标准(FIPS PUB 46)。DES主要采用替换和移位的方法加密,它用56位密钥对64位二进制数据块进行加密,每次加密可对64位数据进行16轮编码,经一系列替换和移位后,输入的64位原始数据转换成完全不同的64位输出数据。
DES对64位的明文分组进行操作。通过一个初始置换,将明文分组分成左半部分和右半部分,各32位长。然后进行16轮完全相同的运算,这些运算被称为函数f,在运算过程中数据与密钥结合。经过16轮后,左、右半部分合在一起,经过一个末置换(初始置换的逆置换),这样该算法就完成了,如图5-3所示。
DES算法的整个体系是公开的,其安全性完全取决于密钥的安全性。该算法中,由于经过了16轮的替换和换位的迭代运算,使密码的分析者无法通过密文获得该算法一般特性以外的更多信息。对于这种算法,破解的唯一可行途径是尝试所有可能的密钥。对于56位长度的密钥,可能的组合达到256=7.2×1016种,想用穷举法来确定某一个密钥的机会是很小的。
可见,对于DNS算法的破解是比较困难的,或者即使能够破解,但是付出的代价相对于破解后所得到的回报过大,也失去了破解的意义。
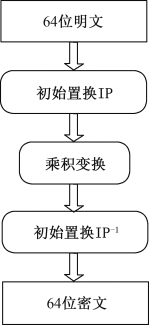
图5-3 DES算法流程
2.IDEA算法
1990年瑞士联邦技术学院的Xuejia Lai(赖学嘉)和James Massey公布了第一版IDEA(International Data Encryption Algorithm,国际数据加密算法),当时称为PES(Proposed Encryption Standard,建议加密标准)。1991年,Biham和Shamir提出了差分密码分析之后,设计者为了抗击此攻击,增加了密码算法的强度,并提出了改进算法IPES(ImprovedProsed Encryption Standard,改进型建议加密标准)。1992年,设计者又将IPES改为IDEA。IDEA是近年来提出的各种分组密码中很成功的算法之一,因为在目前该算法仍然是安全的,它已在PGP(Pretty Good Privacy)中得到应用。
和DES算法一样,IDEA也是对64位大小的数据块进行加密的分组加密算法。输入的明文为64位,生成的密文也为64位。IDEA是一种由8个相似圈和一个输出变换组成的迭代算法。相对于DES算法,IDEA的密钥长度增加到128位,能够有效地提高算法的安全性。IDEA比同时代的算法:FEAL、REDOC-II、LOKI、Snefru等都要坚固,而且到目前为止几乎没有任何关于IDEA密码分析攻击法的成果案例发表,因此目前IDEA的攻击方法只有“直接攻击”或者“密钥穷举”法了。
(二)公钥密码体制
公开密钥加密最初是由Diffie和Hellman在1976年提出的,这是几千年来文字加密的第一次真正革命性的进步。公钥是建立在数学函数基础上,而不是建立在位方式的操作上。更重要的是,公钥加密是不对称的,与只使用一种密钥的对称常规加密相比,它涉及公钥和私钥的使用。这两种密钥的使用已经对机密性、密钥的分发和身份验证领域产生了深远的影响。公钥加密算法可用于数据完整性、数据保密性、发送者不可否认和发送者认证等方面。
公开密钥算法的通信模型如图5-4所示。
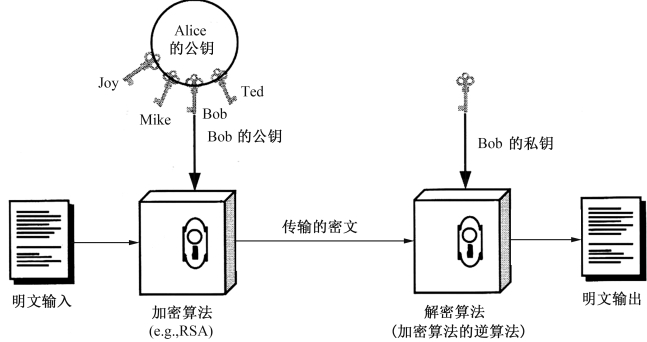
图5-4 公开密钥算法通信模型
由于用户只需要保存好自己的私钥,而对应的公钥无须保密,需要使用公钥的用户可以通过公开的途径得到公钥,因此不存在对称加密算法中的密钥传送问题。同时,n个用户相互之间采用公钥密钥算法进行通信,需要的密钥对数量也仅为n,密钥的管理较对称加密算法简单得多。
公钥密码体制的优缺点如下所述。
(1)优点主要表现在如下三个方面:(www.chuimin.cn)
①网络中的每一个用户只需要保存自己的私钥,则N个用户仅需产生N对密钥。密钥少,便于管理。
②密钥分配简单,不需要秘密的通道和复杂的协议来传送密钥。公钥可基于公开的渠道(如密钥分发中心)分发给其他用户,而私钥则由用户自己保管。
③可以实现数字签名。
(2)缺点:与对称密码体制相比,公钥密码体制的加密、解密处理速度较慢,同等安全强度下公钥密码体制的密钥位数要求多一些。
1.RSA算法
RSA算法是在1977年由美国的3位教授R.L.Rivest(罗纳德李维斯特)、A.Shamirt(阿迪·萨莫尔)和M.Adleman(伦纳德·阿德曼)在题为“获得数字签名和公开钥密码系统的一种方法”中提出的,算法的名称取自3位教授的名字。RSA算法是第一个公开密钥算法,是至今为止最为完善的公开密钥算法之一。RSA算法的这3位发明者也因此在2002年获得了计算机领域的最高奖——图灵奖。
RSA算法基于一些数论的原理,在此不对它做理论上的推导,只说明如何使用这种算法。
选择两个大素数p和q(典型值为大于10100)
计算n=p×q和z=(p-1)(q-1)
选择一个与z互质的数,令其为d
找到一个e使满足ed=1modz
计算以上参数后,就可以对明文加密。首先将明文看成是一个位串,将其划分成一个个的数据块P且0≤P<n。要做到这一点并不难,只需先求出满足2k<n的最大k值,然后,使得每个数据块长度不超过k即可。对数据块P进行加密,计算C=Pe(modn),C即为P的密文;对C进行解密,计算P=Cd(modn)。可以证明,对于指定范围内的所有P其加密函数和解密函数互为反函数。进行加密需要参数e和n,进行解密需要参数d和n,所以公开密钥由(e,n)组成,私人密钥由(d,n)组成。
假设取p=3,q=11,则
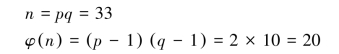
随机选取e,使e与φ(n)互质,取e=3,则可计算出
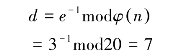
则可得
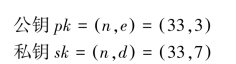
明码报文P的一个密文C,则有C=P3mod33,若明文P=“SUZANNE”,则加/解密过程如表5-1所示。
表5-1 加/解密过程
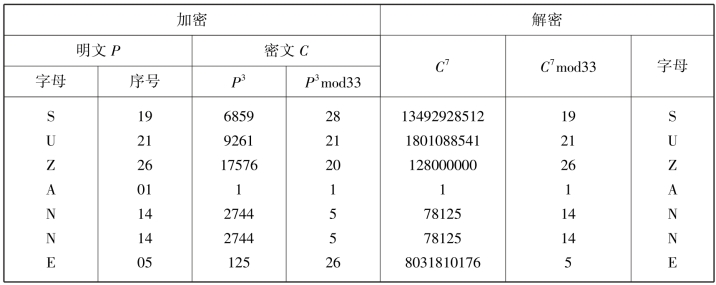
应该指出的是,与对称密码体制DES相比,虽然RSA算法具有安全、方便的特点,但它的运行速度太慢,因此RSA体制很少用于数据加密,而多用在数字签名、密钥管理和认证等方面,数据的加密仍使用秘密密钥算法。
2.Diffie-Hellman算法
Diffie(迪菲)和Hellman(赫尔曼)在1976年首次提出了公开密钥算法的概念,也正是他们实现了第一个公开密钥算法——Diffie-Hellman算法。Diffie-Hellman算法的安全性源于在有限域上计算离散对数比计算指数更为困难。
Diffie-Hellman算法的安全性是基于zp上的离散对数问题。设p是一个满足要求的大素数,并且a(0<a<p)是循环群zp的生成元,a和p公开,所有用户都可以得到a和p。在两个用户A与B通信时,它们可以通过如下步骤协商通信所使用的密钥:
用户A选取一个大的随机数rA(0≤rA≤p-2),计算:![]() ,并且把SA发送给用户B。
,并且把SA发送给用户B。
用户B选取一个m随机数rB(0≤rB≤p-2),计算![]() ,并且把SB发送给用户A。
,并且把SB发送给用户A。
用户A计算![]() ,用户B计算
,用户B计算![]() 。
。
由于![]() ,这样通信双方得到共同的密钥k,就可以实现密钥交换了。
,这样通信双方得到共同的密钥k,就可以实现密钥交换了。
有关计算机网络与信息安全的文章

(一)按防火墙软硬件形式分类如果从软硬件形式来分,防火墙可以分为软件防火墙、硬件防火墙和芯片级防火墙。之所以加上“所谓”二字,是针对芯片级防火墙来说的。目前市场上大多数防火墙都是这种所谓的硬件防火墙,它们都基于PC架构。值得注意的是,由于此类防火墙采用的依然是别人的内核,因此会受到OS本身的安全性影响。应用代理型防火墙工作在OSI的最高层,即应用层。......
2023-10-18

密码学把信息安全核心算法作为其研究目标,其研究内容也随着信息安全不断发展的需求而增长。这里介绍几个有代表性的密码学研究新方向,以及这些算法与传统密码算法相比较的特点。这种思想使密码算法或密码协议的安全性论证比以往的方法更加科学、可信,因此成为密码学研究的一个热点问题。(三)量子密码学量子计算是近年来兴起的一个研究领域。这是量子计算机理论的重大突破,与密码学有重要的联系。......
2023-10-18

为了更好地研究入侵检测系统,人们将其各个组成部分抽象出来,形成各种入侵检测模型。模型中,入侵检测系统分为4个基本组件,即事件产生器、事件分析器、响应单元和事件数据库。其中的事件是指入侵检测系统需要分析的数据。如果入侵检测系统也能够像攻击者那样合作,就有可能检测到。......
2023-10-18

(一)计算机信息隐藏技术的定义在第一届国际信息隐藏会议上达成了信息隐藏的一些基本定义,由Birgit Pfitzmann[1]整理成文。自从20世纪90年代世界各国开始研究信息隐藏技术以来,已有相当数量的研究成果问世,是信息安全领域研究的热点之一。信息隐藏要考虑隐藏的信息在遇到各种环境、操作之后免遭破坏的能力。信息隐藏的数据量与隐藏的免疫力始终是一对矛盾,不存在一种完全满足这两种要求的隐藏方法。信息隐藏技术主要由下述两部分组成。......
2023-10-18

(一)计算机信息隐藏技术的特点信息隐藏技术必须考虑正常的信息操作所造成的威胁,即要使机密资料对正常的数据操作技术具有免疫力。鲁棒性反映了信息隐藏技术的抗干扰能力。(二)计算机信息隐藏技术的分类对信息隐藏技术进行分类的方法有多种,分类方法的不同导致了分类的不同,它们之间既有联系又有区别。......
2023-10-18

(一)计算机病毒的特征计算机病毒是一种特殊程序,这类程序的主要包括以下几个特征。根据病毒的这一特性可将病毒分为良性病毒与恶性病毒。表现和破坏是病毒的最终......
2023-10-18

自此,在密码学领域,数字化混沌密码的研究引起了学者们的注意并掀起了一个小的研究热点。由于混沌理论的不完善和混沌密码研究的不成熟,混沌密码研究曾一度陷入低谷,仅有少量的文献发表。因此,混沌系统符合分组密码设计的原则。这类混沌分组密码往往采用传统分组密码的一些设计结构。与以上介绍的基于混沌的对称密码的研究相比,将混沌系统应用在公钥系统中的研究成果相对较少。......
2023-11-22

链路加密的目的是保护网络节点之间的链路信息安全;端到端加密的目的是对源端用户到目的端用户的数据提供保护;节点加密的目的是对源节点到目的节点之间的传输链路提供保护。因此认清网络的脆弱性和潜在威胁,采取强有力的安全策略,对于保障网络的安全性将变得十分重要。......
2023-10-18
相关推荐