密码体制：加密技术的基本概述

2023-10-18 理论教育版权反馈

【摘要】：（一）密码体制的模型在密码学中，一个密码体制或密码系统是指由明文、密文、密钥、加密算法和解密算法所组成的五元组。加密算法是指在密钥的作用下将明文消息从明文空间映射到密文空间的一种变换方法，该变换过程称为加密，通常用字母E表示，即c=EK。所以，当用户需要与对方发送对称密钥时，只需利用对方公钥加密这个密钥，而这个加密信息只有拥有相应私钥的对方才能解密，得到所发送来的对称密钥。

（一）密码体制的模型

在密码学中，一个密码体制或密码系统是指由明文、密文、密钥、加密算法和解密算法所组成的五元组。

明文是指未经过任何变换处理的原始消息，通常用m（message）或p（plaintext）表示。所有可能的明文有限集组成明文空间，通常用M或P表示。

密文是指明文加密后的消息，通常用c（ciphertext）表示。所有可能的密文有限集组成密文空间，通常用C表示。

密钥是指进行加密或解密操作所需的秘密/公开参数或关键信息，通常用k（key）表示。所有可能的密钥有限集组成密钥空间，通常用K表示。

加密算法是指在密钥的作用下将明文消息从明文空间映射到密文空间的一种变换方法，该变换过程称为加密，通常用字母E表示，即c=EK（m）。

解密算法是指在密钥的作用下将密文消息从密文空间映射到明文空间的一种变换方法，该变换过程称为解密，通常用字母D表示，即m=DK（C）。

图5-1所示为一种最基本的密码体制模型。在对称密码体制中，加密密钥k1和解密密钥k2是相同的，或者虽然两者不相同，但已知其中一个密钥就能很容易地推出另一个密钥。在通常情况下，加密算法是解密算法的逆过程或逆函数。而在非对称密码体制中，作为公钥的加密密钥k1和作为私钥的解密密钥k2在本质上是完全不相同的，已知其中一个密钥推出另一个密钥在计算上是不可行的，并且解密算法一般不是加密算法的逆过程或逆函数。

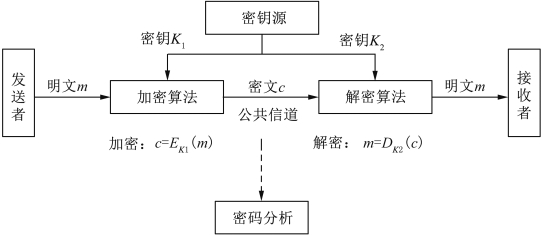
pagenumber_ebook=90,pagenumber_book=84

图5-1　密码体制的基本模型

（二）密码体制的分类

密码体制是指实现加密和解密功能的密码方案，从密钥使用策略上，可分为对称密码体制（Symmetric Key Cryptosystem）和非对称密码体制（Asymmetric Key Cryptosystem）两类，非对称密码体制也被称为公钥密码体制（Public Key Cryptosystem）。

1.对称密码体制

在对称密码体制中，由于加密密钥K1和解密密钥K2是相同的，或者虽然两者不相同，但已知其中一个密钥就能很容易地推出另一个密钥，因此消息的发送者和接收者必须对所使用的密钥完全保密，不能让任何第三方知道。对称密码体制又称为秘密密钥体制（Secret Key Cryptosystem）、单钥密码体制（One Key Cryptosystem）或传统密码体制（Traditional Cryptosystem）。按加密过程对数据的处理方式，它可以分为分组密码和序列密码两类，经典的对称密码算法有AES、DES、RC4和A5等。

（1）对称密码体制的优点

①加密和解密的速度都比较快，具有较高的数据吞吐率，不仅软件能实现较高的吞吐量，而且还适合于硬件实现，使硬件加密和解密的处理速度更快。

②对称密码体制中所使用的密钥相对较短。

③密文的长度往往与明文长度相同。

（2）对称密码体制的缺点

①密钥分发需要安全通道，发送方如何安全、高效地把密钥送到接收方是对称密码体制的软肋，对称密钥的分发过程往往很烦琐，需要付出的代价较高。

②密钥量大，难于管理。多人用对称密码算法进行保密通信时，其密钥量的增长会按通信人数二次方的方式增长，导致密钥管理变得越来越复杂。例如，n个人使用对称密码体制相互通信，总共需要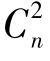 pagenumber_ebook=90,pagenumber_book=84 个密钥，每个人拥有n-1个密钥，当n较大时，将极大地增加密钥管理（包括密钥的生成、使用、存储、备份、存档、更新等）的复杂性和难度。

③难以解决不可否认性问题。因为通信双方拥有相同的密钥，所以接收方可以否认接收某消息，发送方也可以否认发送过某消息，即对称密码体制很难解决鉴别认证和不可否认性的问题。

2.非对称密码体制

在非对称密码体制中，加密密钥和解密密钥是完全不同的，一个是对外公开的公钥，可以通过公钥证书进行注册公开；另一个是必须保密的私钥，只有拥有者才知道。不能从公钥推出私钥，或者说从公钥推出私钥在计算上是不可行的。非对称密码体制又称为双钥密码体制（Double Key Cryptosystem）或公开密钥密码体制（Public Key Cryptosystem）。典型的非对称密码体制有RSA、ECC、Rabin、Elgamal和NTRU等。

非对称密码体制主要是为了解决对称密码体制中难以解决的问题而提出的，一是解决对称密码体制中密钥分发和管理的问题；二是解决不可否认性的问题。由此可知，非对称密码体制在密钥分配和管理、鉴别认证、不可否认性等方面具有重要意义。

对称密码体制主要用于信息的保密，实现信息的机密性。而非对称密码体制不仅可用来对信息进行加密，还可以用来对信息进行数字签名。在非对称密码体制中，任何人可用信息接收者的公钥对信息进行加密，信息接收者则用自己的私钥进行解密。而在数字签名算法中，签名者用自己的私钥对信息进行签名，任何人可用他相应的公钥验证其签名的有效性。因此，非对称密码体制不仅可保障信息的机密性，还具有认证和抗否认性的功能。

（1）非对称密码体制的优点

①密钥的分发相对容易。在非对称密码体制中，公钥是公开的，而用公钥加密的信息只有对应的私钥才能解密。所以，当用户需要与对方发送对称密钥时，只需利用对方公钥加密这个密钥，而这个加密信息只有拥有相应私钥的对方才能解密，得到所发送来的对称密钥。

②密钥管理简单。每个用户只需保存好自己的私钥，对外公布自己的公钥，则n个用户仅需产生n对密钥，即密钥总量为2n。当n较大时，密钥总量的增长是线性的，而每个用户管理密钥个数始终为一个。

③可以有效地实现数字签名。这是因为消息签名的产生来自于用户的私钥，其验证使用了用户的公钥，由此可以解决信息的不可否认性问题。

（2）非对称密码体制的缺点(www.chuimin.cn)

①与对称密码体制相比，非对称密码体制加密/解密速度较慢。

②在同等安全强度下，非对称密码体制要求的密钥长度要长一些。

③密文的长度往往大于明文的长度。

无论是对称密码体制还是非对称密码体制，在设计和使用时必须遵守柯克霍夫原则（Kerckhoffs Principle）：即使密码系统的任何细节已为人悉知，只要密钥未泄露，就应该是安全的。柯克霍夫原则也称为柯克霍夫假设（Kerckhoffs Assumption）或柯克霍夫公理（Kerckhoffs Axiom），它主要阐述了关于密码分析的一个基本假设，任何一个密码系统的安全性不应取决于不易改变的算法，而应取决于密钥的安全性，只要密钥是安全的，则攻击者就无法从密文推导出明文。

（三）密码体制的评价

1.密码算法的评价标准

随着现代密码学的发展，对密码算法的评价虽然没有统一的标准，但从最近的美国国家标准与技术研究院（NIST）对AES候选算法的选择标准来看，对密码算法的评价标准主要集中在以下几个方面。

（1）安全性：安全是最重要的评价因素。

（2）计算的效率：即算法的速度，算法在不同的工作平台上的速度都应该考虑到。

（3）存储条件：对RAM和ROM的要求。

（4）软件和硬件的适应性：算法在软件和硬件上都应该能够被有效地实现。

（5）简洁性：要求算法容易实现。

（6）适应性：算法应与大多数的工作平台相适应，能在广泛的范围内应用，具有可变的密钥长度。

也可以概括性地认为密码算法评价的标准分为安全、费用和算法的实施特点三大类。其中，安全包括坚实的数学基础，以及与其他算法相比较的相对安全性等；费用包括在不同平台的计算速度和存储必备条件；算法的实施特点包括软件和硬件的适应性、算法的简洁性，以及与各种平台的适应性、密钥的灵活性等。

2.安全密码体制的性质

安全性对密码体制尤为重要，从前面密码体制的攻击可以看到，一个安全的密码体制应该具有以下性质。

（l）从密文恢复明文应该是难的，即使分析者知道明文空间（如明文是英文）。

（2）从密文计算出明文部分信息应该是难的。

（3）从密文探测出简单却有用的事实应该是难的，如相同的信息被发送了两次。

3.密码体制攻击的结果

从密码分析者对一种密码体制攻击的效果来看，它可能达到以下结果。

（l）完全攻破。密码分析者找到了相应的密钥，从而对任意用同一密钥加密的密文恢复出对应的明文。

（2）部分攻破。密码分析者没有找到相应的密钥，但对于给定的密文，敌手能够获得明文的特定信息。

（3）密文识别。如对于两个给定的不同明文及其中一个明文的密文，密码分析者能够识别出该密文对应于哪个明文，或者能够识别出给定明文的密文和随机字符串。如果一个密码体制使得敌手不能在多项式时间内识别密文，这样的密码体制称为达到了语义安全（Semantic Security）。

4.评价密码体制的途径

评价密码体制安全性有不同的途径，包括无条件安全性、计算安全性、可证明安全性。

（l）无条件安全性。如果密码分析者具有无限的计算能力，密码体制也不能被攻破，那么这个密码体制就是无条件安全的。例如，只有单个的明文用给定的密钥加密，移位密码和代换密码都是无条件安全的。一次一密加密（One-Time Pad Cipher）对于唯密文攻击是无条件安全的，因为敌手即使获得很多密文信息，具有无限的计算资源，仍然不能获得明文的任何信息。如果一个密码体制对于唯密文攻击是无条件安全的，则称该密码体制具有完善保密性。如果明文空间是自然语言，所有其他的密码系统在唯密文攻击中都是可破的，因为只要简单地一个接一个地去试每种可能的密钥，并且检查所得明文是否都在明文空间中。这种方法称为穷举攻击（Brute Force Attack）。

（2）计算安全性。密码学更关心在计算上不可破译的密码系统。如果攻破一个密码体制的最好算法用现在或将来可得到的资源都不能在足够长的时间内破译，这个密码体制被认为在计算上是安全的。目前还没有任何一个实际的密码体制被证明是计算上安全的，因为我们知道的只是攻破一个密码体制的当前的最好算法，也许还存在一个我们现在还没有发现的更好的攻击算法。实际上，密码体制对某一种类型的攻击（如穷举攻击）在计算上是安全的，但对其他类型的攻击可能在计算上是不安全的。

（3）可证明安全性。另一种安全性度量是把密码体制的安全性归约为某个经过深入研究的数学难题。例如，如果给定的密码体制是可以破解的，那么就存在一种有效的方法解决大数的因子分解问题，而因子分解问题目前不存在有效的解决方法，于是称该密码体制是可证明安全的，即可证明攻破该密码体制比解决大数因子分解问题更难。可证明安全性只是说明密码体制的安全与一个问题是相关的，并没有证明密码体制是安全的。可证明安全性有时候也被称为归约安全性。

密码体制：加密技术的基本概述

相关推荐