时空配准运动插值方法在虚拟现实应用中的实践

2023-10-17 理论教育版权反馈

【摘要】：我们研究基于时空配准的运动插值算法，解决人体运动的参数插值问题，包括时间配准、空间配准、帧插值和约束重建四个步骤。下面以两个运动M1、M2为例，介绍基于时空配准的运动插值算法。图5-13显示了采用贪心算法得到的配置曲线的效果图。严格来说，方位配准曲线与时间配准曲线完全不同，并非一条坐标系下的曲线，而是基于时间配准曲线的一系列数值。

我们研究基于时空配准的运动插值算法，解决人体运动的参数插值问题，包括时间配准、空间配准、帧插值（根结点位置插值和关节角度插值）和约束重建四个步骤。

下面以两个运动M1、M2为例，介绍基于时空配准的运动插值算法。

1）时间配准

我们利用距离函数D（F1，F2）来衡量两帧F1和F2的运动姿态的相似程度，其中D（F1，F2）的计算方法参见［67］。我们可以用一个二维图像的结构来形象地表示两运动相似性计算结果，用横坐标代表第一个运动，横坐标i对应第一个运动的第i帧，用纵坐标代表第二个运动，纵坐标j对应第二个运动第j帧，每个像素点都对应一个值，坐标（i，j）对应的像素点的值就是第一个运动的第i帧与第二个运动的第j帧之间的距离值。两个运动距离值对应的图像如图5-10所示。

给定图上的两个点，Kovar和Gleicher［64］采用动态规划算法寻找这两个点之间的全局最优路径，且同时满足连接性、单调性和倾斜限制约束。

因为动态规划本身的算法复杂度较高而且相似度计算比较耗时，所以确定配准曲线需要大量计算时间，从而也就延长了运动图的构建时间。假设M1有r1帧，M2有r2帧，即使所有不可达的点不需要计算代价值，但动态时间配准的时间复杂度也有O（r1r2）。考虑到这一点，我们可以用一种贪心算法代替动态规划，得到近似最优的配准曲线，减少构建时间。

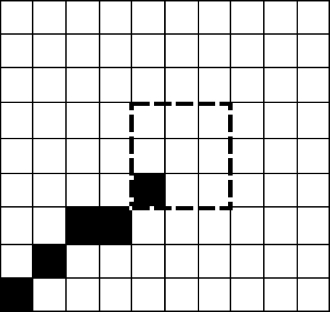
pagenumber_ebook=70,pagenumber_book=63

图5-10　距离图

pagenumber_ebook=70,pagenumber_book=63

图5-11　连续使用3×3窗口寻找路径

这种贪心算法的思想是从起始点c开始，在小规模的子图内寻找最优路径确定子图内的终止点c′，在以c′为起始点在对应的子图内寻找终止点c″，继续迭代直到在右边缘或下边缘寻找到终止点作为整个曲线的终止点c～。我们以窗口长度k＝3的情况为例说明这种方法，以起始点c作为左下角点，在规模3×3的子图内寻找最优路径，确定子图内的终点c′，再以这个c′为起始点在下一个子图内寻找最优路径，继续迭代直到在右边缘或下边缘找到终止点c～，寻找路径的示意图如图5-11所示。

在子图内寻找最优路径时也要考虑到连接性、单调性和倾斜限制，子图内的可选路径是有限的，以倾斜限制W＝3为例，3×3子图内的可选路径只有五种情况（见图5-12）。在判断是否是可选路径时需要注重的一点是，要保证在这个子图上确定的路径结合下一个子图的路径的结果也不会违反倾斜限制。

pagenumber_ebook=70,pagenumber_book=63

图5-12　窗口长度为3时的可选路径

贪心算法的时间复杂度只有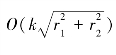 pagenumber_ebook=70,pagenumber_book=63 ，因为只需要计算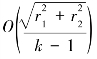个子图，每个子图的时间复杂度是O（k2）。经过大量实验验证，窗口长度k＝3一般可以得到很好的配准曲线，插值结果也很自然。图5-13显示了采用贪心算法得到的配置曲线的效果图。

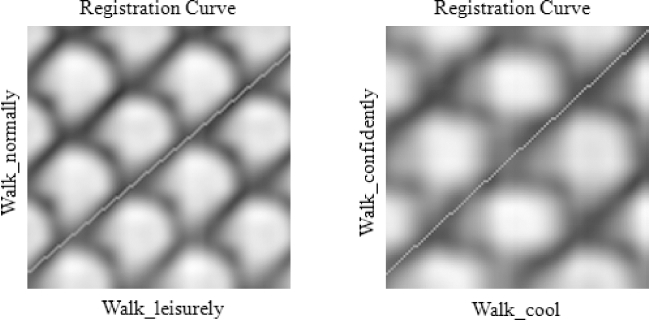
pagenumber_ebook=71,pagenumber_book=64

图5-13　时间配准曲线

2）空间配准

时间配准曲线S（u）一旦确定下来，方位配准曲线A（u）也可以随之很快生成，方位配准曲线A（u）的生成方法是找到S（u）上每个点对应的两个帧对齐时需要的刚性变换。

严格来说，方位配准曲线与时间配准曲线完全不同，并非一条坐标系下的曲线，而是基于时间配准曲线的一系列数值。它的目的是将地面上的两个不同方向和姿态的运动通过坐标变换移到相同的位置，而它的值就是这个坐标变换。对于两个运动M1和M2，时间配准曲线上第i个点对应的两个帧表示为｛M1（t1i），M2（t2i）｝，那么方位配准曲线上第i个点对应的值就是求出把M2（t2i）对齐M1（t1i）时的刚性变换参数｛θi，x0i，z0i｝。为了保证角度变化的连续性，需要对旋转角度参数做调整，使其满足｜θi－θi－1｜≤π，再进一步用空间二次B样条曲线拟合的方位曲线修正结果。

3）帧插值(www.chuimin.cn)

根据配准曲线来插值生成单独的一帧运动B（ti）的方法如下：先找到时间配置曲线上对应点S（ui），根据方位配准曲线对应的点A（ui）的值来对齐S（ui）点对应的两帧，之后按权重w（ti）来计算加权平均值，最后加入各种约束。

我们假定对于插值帧B（t0）、u0的值是已经知道的。这个帧首先创建，然后按照时间顺序产生其他的帧：假设B（t0）不是第一个插值帧，而是我们需要插值的帧序列中的某一中间帧，那么我们需要首先创建前向帧（B（t1），B（t2），…），然后创建后向帧（B（t－1），B（t－2），…）。我们需要u（t）严格递增，这样在插值时间t不断向前的情况下，全局时间t也会持续向前。

下面给出前向顺序下产生插值帧的过程，相反方向产生帧的情况类似处理。

（1）沿配准曲线前进。对于k个输入待混合运动，我们利用

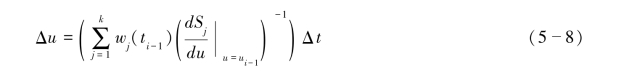
pagenumber_ebook=71,pagenumber_book=64

来计算全局时间参数u向前流动的速度，它是根据输入运动时间配准曲线变化率的插值权重组合而得。

（2）帧的定位和朝向。一旦ui定下来后，可以从输入的运动中提取出帧序列Mj（Sj（ui）），且每个帧的原始配置是用Aj（ui）进行转换的。这样就产生了一组相互匹配的帧，使得可以通过一个变换T（ti）在地面上进行移位和旋转。这种情况下，整个变换应用到Mj（Sj（ui））上，则我们的变换矩阵是T（ti）Aj（ui）。对于插值的第一帧，T（t0）可以任意选择。对于其他帧，T（ti）的选择必须使得B（ti）的位置和朝向与前一帧B（ti－1）一致。具体来说，临时假定wj（t）是1且对于t＞ti－1的所有的插值权重都是0。则剩下的插值应该是简单地用T（ti－1）Aj（ui－1）对Mj的一部分进行直接拷贝和变换，所以它和B（ti－1）可以光滑的衔接在一起。如果ΔTj（ti）定义为

然后设置T（ti）＝ΔTj（ti）就得到这个结果。

更一般的，每个运动Mj会对T（ti）进行表决，即衡量他们相对局部坐标系统不变（也就是，ΔTj（ti））的程度，然后这个表决结果根据插值权重进行平均。为了进行平均，必须选择恰当的参数来表示ΔTj（ti）。我们的算法是首先在需要变换的帧序列的中心附近计算一个起始点。特别的，每个Mj（Sj（ui））都用ΔTj（ti）Aj（ui－1）进行转换过，这样新的根节点的位置就被投影到地面且被统一了。然后ΔTj（ti）采用参数集合｛φj，xj，zj｝来表示，代表的意义是对应于这个起始点旋转φ后平移（xj，zj）。最终，T（ti）是：

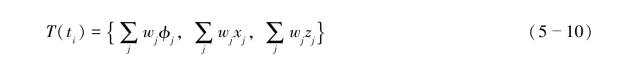
pagenumber_ebook=72,pagenumber_book=65

（3）创建插值帧。经过上两步操作，我们已经能够从输入运动中提取出帧序列并且把他们放置在恰当的位置和旋转角度，可以通过当前的插值权重来计算输出节点参数的加权平均，进而形成插值后的骨架造型。为了计算平均旋转角度，需要首先计算一个参考旋转角度qref，来最小化输入旋转角度qi的距离。每个qi随后变换到qref的局部坐标帧中，并且转化成一种对数映射的表示方式，然后对这些对数映射后的值进行平均化。最后，再次通过指数映射并变换回全局坐标来找到平均转角q－：

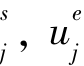pagenumber_ebook=72,pagenumber_book=65