归纳原理与实数连续性之等价性

2023-10-17 理论教育版权反馈

【摘要】：连续归纳法用于实数系是否成立，自然要依赖于实数系的基本性质。实数系与有理数系的根本不同，在于实数系的连续性。我们要证明的是命题8.2.1 连续归纳法等价于关于实数完备性的戴德金公理。设连续归纳法成立，如果已把全体实数分成了非空的甲、乙两集，而且甲集中任一个数小于乙集中的每个数，要证明的是甲集有最大数或乙集有最小数。由连续归纳法，可知px对一切x真，即一切实数x属于甲集。

连续归纳法用于实数系是否成立，自然要依赖于实数系的基本性质。

实数系与有理数系的根本不同，在于实数系的连续性。用一根直线来表示实数系，这条数直线是天衣无缝的。

什么叫天衣无缝呢？如果我们用一把锋利的刀把直线砍断，这一刀，一定砍在某个点A上。若是砍在缝隙上，岂不是有缝了？问题是：数直线被砍断以后，被刀砍中的那个点A到哪里去了呢？它在左半截上，还是在右半截上呢？

回答只能是：不在左边，就在右边（如图8-1）！反正不会两边都有，也不会两边都没有。因为点不可分割，也不会消失！

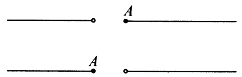
pagenumber_ebook=171,pagenumber_book=159

图8-1

把这一套想法转换成严格的数学语言，便是

关于实数系完备性的戴德金公理如果把全体实数分成甲、乙两个非空数集合，而且甲集里的每一个数x比乙集里任一个数y都小，那么，要么甲集里有最大数，要么乙集里有最小数，二者必居其一，且仅居其一。

我们要证明的是(www.chuimin.cn)

命题8.2.1 连续归纳法等价于关于实数完备性的戴德金公理。

证明：首先用戴德金公理导出连续归纳法，用反证法。若连续归纳法不成立，则有一个涉及实数x的命题px，使归纳法陈述中的（1）和（2）都成立，但仍有x*使p*x不真。于是约定：若对一切x∈（－∞，y）有px真，则y属于甲集；其余的实数属于乙集。显然，甲、乙两集均非空。这是因为归纳法陈述中的（1）保证了甲集非空，而反证法假设 pagenumber_ebook=172,pagenumber_book=160 不真，则保证了乙集非空。由甲集的做法可知甲集中每一个数比乙集中任一数小，由戴德金公理，甲集有最大数或乙集中有最小数，记此数为a。

对任－x∈（－∞，a），由于y0＝＜a，故y0是甲集元素，而x∈（－∞，y0），由甲集定义知px真，即对于一切x＜a有px真。由归纳法陈述中的（2）有δ＞0，使px对一切x＜a+δ为真，这推出了a+δ也属于甲集，这与“a是甲集最大数或乙集最小数”矛盾。从而否定了反证法的假设。

下面再由连续归纳法推出戴德金公理。设连续归纳法成立，如果已把全体实数分成了非空的甲、乙两集，而且甲集中任一个数小于乙集中的每个数，要证明的是甲集有最大数或乙集有最小数。

用反证法。设甲集无最大数且乙集无最小数。约定命题px的意义是“x属于甲集”。因甲集不空，甲集中有某数x0，于是对一切x∈（－∞，x0），x属于甲集，即px真，这就有了“归纳起点”。

设对一切x∈（－∞，y）有px真。由于乙集中没有最小数，故y必属于甲集。又因甲集中无最大数，故有δ＞0使y+δ也属于甲集，从而对一切x∈（－∞，y+δ）有px真。这完成了“归纳推断”。

由连续归纳法，可知px对一切x真，即一切实数x属于甲集。这与乙集非空矛盾。

现在已经弄明白了：就像常用的数学归纳法可以作为一条自然数的公理一样，连续归纳法也可以作为实数的公理，用它取代戴德金公理或其他形式的等价的实数连续性公理。

归纳原理与实数连续性之等价性

相关推荐