定义7.3.3设{an}是无穷数列。用“ε-语言”,不仅能够引入极限概念,还能证明与极限有关的一系列基本定理,直接计算一些具体的极限。实践证明确实有效,而且比用“ε-语言”还要简便![例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例,说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列,{Ln}为有界数列。......
2023-10-17
既然讲数列极限可以不用“ε-语言”,那么讲函数极限也可以不用“ε-语言”,只不过用“无界不减函数”代替“无界不减数列”罢了。
定义7.4.1 设D(x)是在[c,+∞)上有定义的函数。如果D(x)是单调不减的(即当x1<x2时有D(x1)≤D(x2)),并且是无界的(即不存在M>0使不等式|D(x)|≤M对一切x∈[c,+∞)成立),就称D(x)是+∞邻域的无界不减函数。
无界不减函数,是一个很简单、很明确的概念。有了它,便可以对函数引入无穷大、无穷小及极限概念了。
定义7.4.2 设f(x)是在[c,+∞)上有定义的函数。如果有一个在+∞邻域无界不减的函数D(x),使不等式
|f(x)|≥D(x)
对某个区间[A,+∞)上的一切x成立,则称f(x)在x趋于+∞时趋于∞,记作
或
f(x)→∞(x→+∞)。
有了无穷大,如法炮制,无穷小就有了。
定义7.4.3 设f(x)在[c,+∞)上有定义。若有一个在+∞邻域无界不减的恒正函数D(x),使不等式
对某个区间[A,+∞)上的一切x成立,则称f(x)是x→+∞过程中的无穷小量,或说当x趋于+∞时f(x)趋于0。记作
或
有了无穷小的概念,极限的概念自然也就产生了。
定义7.4.4 设f(x)在[c,+∞)有定义。如果有实数a,使f(x)-a是x→+∞过程中的无穷小量,则称f(x)当x→+∞时以a为极限,记作
或
现在,我们已引入了函数的无穷大、无穷小以及极限概念。事实上,我们只不过是用x代替了数列里的n罢了。连续变量x和离散变量n有共同点,它们都会趋于+∞;但又有不同点:x还可以趋于0,趋于1,趋于任一实数x0。这样一来,函数极限就比数列极限花样更多。用“ε-语言”讲函数极限,常常要一条一条分别给出各种过程中的极限定义。我们则不用那么麻烦,只要用一下代数式的变换,就足以定义出新的极限过程了。
定义7.4.5 若f(x)在(x0,x0+δ]上有定义(这里δ是某个正数),则
定义为
作变换y=![]() 之后,即
之后,即
定义7.4.6 若f(x)在[x0-δ,x0)上有定义(这里δ是某个正数),则
定义为
作变换y=![]() 之后,即
之后,即
定义7.4.7 若同时有
则称
这就把函数的极限给出来了。
当然,也可以不依赖左、右单边极限而直接定义函数的双边极限。例如,可以把(7.4.1)式定义为(www.chuimin.cn)
作变换y=![]() 后即
后即
而这里把“y→∞”理解为|y|→+∞就可以了。
此外,还可以引入![]() ,即
,即
而
同时成立时就说
这比把![]() 简单地定义为
简单地定义为![]() 要更明确、更严格。在极限概念
要更明确、更严格。在极限概念![]() =a中,x不能取值x0,而f(x)可取值a,这个道理学生往往想不通。因为在一般分析教程中,它是作为一条规定颁布下来的,没有什么理由可讲。但在我们这里,由于
=a中,x不能取值x0,而f(x)可取值a,这个道理学生往往想不通。因为在一般分析教程中,它是作为一条规定颁布下来的,没有什么理由可讲。但在我们这里,由于![]() 是用
是用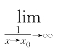 来定义的,x就自然不能取值x0了。否则,分母就出现了0而使表达式失去了意义。
来定义的,x就自然不能取值x0了。否则,分母就出现了0而使表达式失去了意义。
这一套定义,将使学生在学习微积分时免受“ε-语言”之累,在定理证明和做题时用代数运算代替逻辑推理。
[例7.4.1] 求证:![]() =+∞。
=+∞。
证明:当x>4时有
因D(x)=![]() 是无界不减的,即得证。
是无界不减的,即得证。
[例7.4.2] 求证:![]() =0。
=0。
证明:因在[0,+∞)上有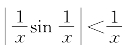 ,由D(x)=x无界不减得知
,由D(x)=x无界不减得知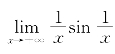 。又在(-∞,0]上有
。又在(-∞,0]上有
按定义得
或可以简单地由 即得所要结论。
即得所要结论。
[例7.4.3] 求![]() 。
。
解:
因为
又因![]() 在[1,+∞)上无界不减,所以
在[1,+∞)上无界不减,所以
按定义得
[例7.4.4] 求证:![]() 。
。
证明:要证的实际上是
按定义,
这最后一步是因为
而![]() (y+2)在[-2,+∞)上无界不减。
(y+2)在[-2,+∞)上无界不减。
为了叙述方便,不妨称这里引入的极限定义为“D-语言”。这种定义的特点是把任意极限问题化为无穷大问题,再用一个无界不减列Dn或无界不减函数D(x)来比较,定义本身就是一个判别法。
有关从数学教育到教育数学的文章

定义7.3.3设{an}是无穷数列。用“ε-语言”,不仅能够引入极限概念,还能证明与极限有关的一系列基本定理,直接计算一些具体的极限。实践证明确实有效,而且比用“ε-语言”还要简便![例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例,说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列,{Ln}为有界数列。......
2023-10-17

之所以说十进制并非尽善尽美,我们有更有力的理由:因为还有比十进制记数法更优越的方法。充分利用这5个指头,能造出更好的记数法来。这种记数法的好处,不仅在于少用了6,7,8,9这4个数码,更重要的是运算起来方便。比方说,3.68在新记数法里是,截尾之后得到,恰好是3.7,相当于把3.68最后的8进上去。可见,十进制记数法虽然是一份珍贵的遗产,同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17

数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮,席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学,而不是数学本身。于是,数学教育学要靠数学提供材料。为了数学教育的需要,对数学成果进行再创造,这已不是数学教育学的任务了。这主要是数学工作者的责任,是数学的任务。......
2023-10-17

为底的对数——自然对数。若用曲线y=下的面积引入自然对数lnx,则显得简单具体、直观性强,而且涉及的基础知识少,还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ>0,有①也可不用压缩变换,直接用求导方法证明sx1=sλxλ。至此,可以引入自然对数了。定义6.3.2对0<x<+∞,记=lnx,并称函数y=lnx为x的自然对数。从两个定义及三个推论中,立刻得到自然对数的一系列性质。......
2023-10-17

有了连续归纳法,数学分析里的一系列涉及实数连续性和连续函数性质的定理,就可以用统一的模式来证明。以下用连续归纳法证明:这将推出每个实数都是{bn}的下界,即得矛盾。由连续归纳法,px对一切x成立。[例8.3.6]设f在[a,b]上连续,f<0,f>0,则至少有一个点x0∈(a,b),使f=0。[例8.3.7]若f在[a,b]上连续,则f在[a,b]上取到最大值和最小值。......
2023-10-17

命题5.4.1设M、N两点在直线AB的同侧,则MN∥AB的充分必要条件是△MAB=△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q,若同位角相等,则AB∥CD。于是,共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中,有∠A=∠A′或∠A+∠A′=180°,则。命题5.4.5PQ∥AB,若直线l与AB垂直,则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2,而l3与l1、l2相截,则内错角相等。......
2023-10-17

前面的几个例子都有这个特点:利用一点邻域的性质来推出全局的性质。抓住这一点,便能建立一个统一的推理模式,使许多定理的证明简化。我们引入一个“可分命题”的概念。可分命题 设命题Q△是涉及区间△的一个判断,如果满足下面两条:若Q△成立,且△1△,则Q△成立。使用定理Q,一定要把所要证的命题设法转化成一个有关的可分命题。下面,我们用上一节的例题来说明这种推理模式的用法。推证方法同确界存在定理,用反证法。......
2023-10-17

定义4.3.1 边长为1,有一个角为α的菱形的面积,叫做角α的正弦,记作sinα=Sα。命题4.3.1在△ABC中,设BC=a。把三角形面积公式各项同除以,立刻得到:正弦定理 在任意△ABC中,有这个定理的用处之大是众所周知的。在式中,我们取α+β=90°,可立刻得到重要的命题。这样,为“余角的正弦”创设一个新符号将十分方便,余弦应运而生:定义4.3.2一个角α的余角的正弦,叫做α的余弦,记作cosα。......
2023-10-17
相关推荐