珍贵遗产：微积分的重要性

2023-10-17 理论教育版权反馈

【摘要】：确实，微积分学是前人留给我们的科学文化遗产中最珍贵的瑰宝之一。当牛顿创立微积分时，这一崭新的强有力的数学方法的基础是极不完善的。微积分方法的灵魂是“无穷小”。但是，对“无穷小”的攻击与嘲讽，依然同暴风雨般向初生的微积分袭来。以此为基础，极限理论也终于建立起来，这为微积分大厦提供了坚实的基础。微积分，这又是前人留下的一份珍贵遗产，而且是我们必须继承的遗产。

恩格斯说过：在一切理论成就中，未必有什么像17世纪下半叶微积分的发明那样，被看做是人类精神的最高胜利了。

确实，微积分学是前人留给我们的科学文化遗产中最珍贵的瑰宝之一。许多用算术、几何与代数方法无法解决的数学问题，都被微积分摧枯拉朽般地征服了。

当牛顿创立微积分时，这一崭新的强有力的数学方法的基础是极不完善的。微积分方法的灵魂是“无穷小”。那么，牛顿是怎样把“无穷小”作为道具，进行精彩表演的呢？

牛顿是从研究变速运动物体的速度计算问题来引入无穷小的。

比方说，一个小球从空中下落，越落越快，它的速度时时在变化。经过t秒钟，它下落的距离是

这个式子叫做小球的运动方程式。知道了运动方程式，如何计算小球在每个时刻t的运动速度呢？

从时刻t到时刻t+h，小球走过的距离是容易算出来的，就是

把这段距离用这段时间h去除，便算出了在时间区间[t，t+h]内小球的平均速度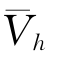 pagenumber_ebook=151,pagenumber_book=139 ，

然后让h＝0，就得到了小球在时刻t的瞬时速度v（t）＝gt。

推理进行得似乎很顺利，但是我们细心检查一下，就会发现一个逻辑上的漏洞：

在推导（7.1.1）式时，要用h做分母，所以必须假定h≠0。但为了得到时刻t的瞬时速度，又必须让h＝0。那我们怎么知道（7.1.1）式在h＝0时成不成立呢？

牛顿当然看到了这个逻辑上的漏洞，于是他请“无穷小”来帮忙。他用记号“o”代替h，这个“o”就是无穷小，于是（7.1.1）式被改写成：

牛顿说，“o”很小很小，比任何正数都小，但它不是0。因为不是0，所以可以做分母，来完成（7.1.2）前一部分的推导；又因为它比任何正数都小，所以它可以忽略不计，这又完成了（7.1.2）后一部分的推导。

用这种办法，牛顿和他同时代的数学家们取得了辉煌的成就，解决了大量有实际意义的问题。(www.chuimin.cn)

但是，对“无穷小”的攻击与嘲讽，依然同暴风雨般向初生的微积分袭来。人们问：这个“o”究竟是什么？它到底是不是0？如果是0，就不能当分母；如果不是0，就不能任意略去！其中攻击得最激烈的，要算18世纪英国的贝克莱主教了。他发表了一篇题为《分析学者——致一个不信神的数学家》的长文，尖锐地指出“无穷小是什么”这个切中要害的问题。他尖酸刻薄地把无穷小的比值叫做“消失了的量的鬼魂”，并且质问数学家：“既然相信这些量的鬼魂，又有什么理由不相信上帝呢？”