为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。......
2023-10-17
数学教育中的余面积与勾股差
【摘要】：基于余面积及勾股差的概念，我们可以把勾股定理的古希腊证法推广为余弦定理的一个证法。这时有图6-25以及由此解出这就证明了以勾股定理为特款的余弦定理。由定义及前面推出的余面积公式，可得到勾股差的基本性质勾股差PABC＝0的充分必要条件是：两点A、B重合，或B、C重合，或∠ABC为直角。[例6.5.1]已知△ABC的三边a、b、c，求此三角形面积。[例6.5.3]如图6-29，设△ABC的两高AD与CE交于H，求证：BH⊥AC。
前面我们引进了一个十分有用的三角形面积公式△ABC＝
acsinB，对它适当地加以变化，看看有没有新收获。
把公式中的sinB换成cosB，会得到另一个与△ABC有关的量
accosB。为了方便，给它取个名字，叫做△ABC关于∠B的“余面积”，记作
＝
accosB。
我们马上可以看出，三角形的面积跟余面积有很大的不同。对面积而言，有
不论用哪个角的正弦来算，结果都一样。对余面积就不一样了，3个量
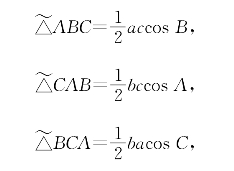
一般说来是两两不同的。也就是说，三角形的面积只有一个，而余面积却有三个！
从几何图形上看，余面积又是怎么回事呢？如图6-22，在△ABC（当∠ABC≤90°时）的一边BC上，画个正方形BCPQ，则
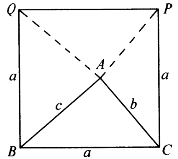
图6-22
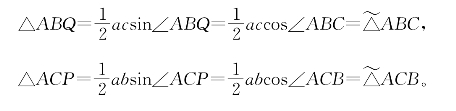
因为△ABQ与△ACP之和恰好是正方形BCPQ面积的一半，所以当∠ABC、∠ACB都不是钝角时有
如果∠ABC、∠ACB中有一个为钝角，该式也成立。如图6-23，有
图6-23
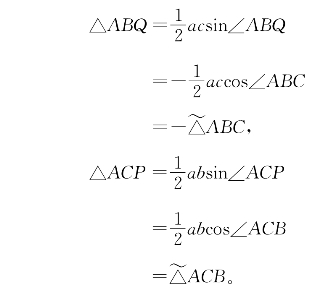
由于△ACP－△ABQ等于正方形BCPQ面积的一半，则
此即（1）式。
按定义，
与
是一样的，所以可以简单地记作
即
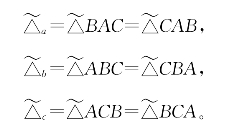
这样，（1）式可以简单地表示为
改换字母又得
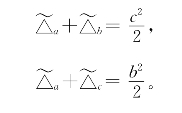
三式联立，解得
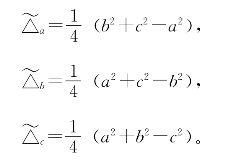
我们把b2+c2－a2叫做△ABC中关于∠A的勾股差，则上面的结果可叙述为：
余面积公式 在任意三角形ABC中，关于某角的余面积，等于该三角形中关于此角的勾股差的
。
按余面积的定义可知，余面积公式其实是余弦定理的另一种形式。
基于余面积及勾股差的概念，我们可以把勾股定理的古希腊证法推广为余弦定理的一个证法。一般中学几何课本上都有勾股定理的古希腊证法。如图6-24，在直角△ABC的三条边上各作一正方形，有
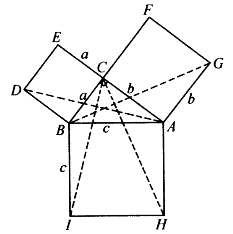
图6-24
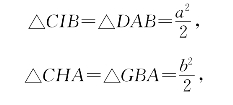
又有
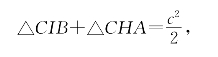
这就证明了勾股定理。
现在考虑一般的情形，如图6-25，三角形ABC是任意三角形（图中画出的是一个锐角三角形。关于钝角三角形的情况，证法类似，只要注意到某些正号改为负号，以及钝角余弦为负的规律即可）。这时有
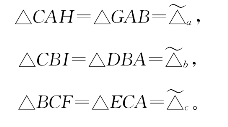
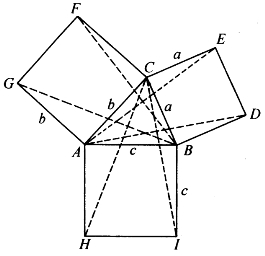
图6-25
以及
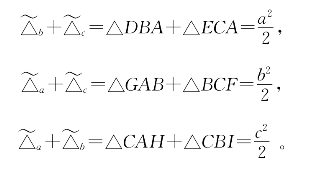
由此解出
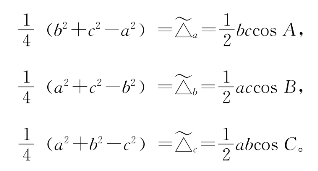
这就证明了以勾股定理为特款的余弦定理。
以下用记号PABC记△ABC关于∠B的勾股差。这里包括了△ABC退化的情形。也就是说，我们有
关于三点勾股差的定义 对任意3点A、B、C，勾股差PABC定义为：
PABC＝AB2+BC2－AC2。
由定义及前面推出的余面积公式，可得到
勾股差的基本性质
（1）（勾股定理）勾股差PABC＝0的充分必要条件是：两点A、B重合，或B、C重合，或∠ABC为直角。
（2）PABC＝PCBA。
（3）PABC+PACB＝2BC2。
（4）（余弦定理）PABC＝2AB·BC·cos∠ABC。
（5）（勾股差定理）若∠ABC＝∠XYZ，则由（4）可得
特别地，当PABC≠0时有
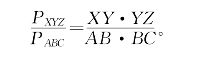
在解几何题时，如涉及垂直、角度大小、线段长短等图形性质，勾股差是一个有用的工具。下面就来举两个例子。
[例6.5.1] 已知△ABC的三边a、b、c，求此三角形面积。
解：设此三角形面积为△，则由面积公式及勾股差的性质可得
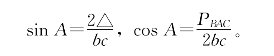
两式平方相加，由sin2A+cos2A＝1得
所以
也就是
这正是秦九韶的三斜求积公式，即海伦公式的另一种形式。
[例6.5.2] 在△ABC的一边BC上取一点P，使BP＝λBC，求AP的长度。(www.chuimin.cn)
解：如图6-26，∠ABP＝∠ABC，用勾股差定理可得
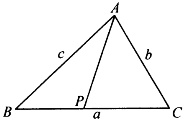
图6-26
也就是
c2+λ2a2－Ap2＝λ（c2+a2－b2），
所以
AP2＝（λ2－λ）a2+Ab2+（1－λ）c2。
勾股差的概念来自余面积，而余面积概念又来自三角形面积公式。但勾股差的性质与面积性质有一个大的差别：一个三角形只有一个面积，却有三个勾股差！这就给勾股差的运用带来不便。有趣的是，如果引入四点勾股差，就可以使它和面积有更多的相似之处。
四点勾股差的定义 对任意四点A、B、C、D，四点勾股差PABCD定义为：
PABCD＝AB2－BC2+CD2－DA2。
利用余弦定理容易说明此定义的几何意义。设AC、BD交于O，设∠AOB＝θ，则
PABCD＝2AC·BDcosθ。
由此定义立刻会得到有关四点勾股差的一些基本性质：
（6）四点勾股差与四边形带号面积的类似性之一
（7）四点勾股差与四边形带号面积的类似性之二
（8）四点勾股差与四边形带号面积的类似性之三
PAABC＝－PBAC，PABBC＝PABC，
PABCC＝－PACB，PCABC＝PACB。
（9）（一般勾股定理）PABCD＝0的充分必要条件是：两点A、C重合，或B、D重合，或AC⊥BD。
性质（9）的证明
先证充分性 若A与C重合，或B与D重合，显然有PABCD＝0。这只要按定义计算即可。当AC⊥BD时，如图6-27，设直线AC、BD交于O，则由勾股定理得：
AB2＝AO2+BO2，
BC2＝BO2+CO2，
CD2＝CO2+DO2，
DA2＝DO2+AO2。
于是得
PABCD＝AB2－BC2+CD2－DA2＝0，
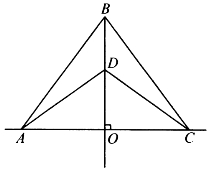
图6-27
图6-28
充分性得证。
再证必要性 不妨设A、C不重合，分别自B、D向AC引垂线，垂足为P、Q（如图6-28）。于是，由勾股定理可得
由此可见，当PABCD＝0时，或者是AC＝0，或者是QP＝0。而当QP＝0时，或者B、D重合，或者BD⊥AC，必要性亦获证。
由性质（9）的证明过程，得到四点勾股差鲜明的几何意义：
（10）（勾股差与投影的关系）当A、C两点不重合时，分别以P、Q记B、D在直线AC上的投影，则
PABCD＝2AC·QP。
由此出发，又可得到关于四点勾股差的一些有用的性质：
（11）勾股差的可分性
PABCD＝PABCE+PAECD。
证明：分别以P、Q、R表示B、E、D在AC上的投影，则由（10）得
下面的性质，十分有助于勾股差的计算：
（12）若BX⊥AC，DY⊥AC，则
PABCD＝PAXCY。
证明：这是因为B、X两点在AC上的投影相同，D、Y两点在AC的投影也相同。
下面举两个例子来说明四点勾股差的应用。
[例6.5.3] 如图6-29，设△ABC的两高AD与CE交于H，求证：BH⊥AC。
证明：只要证明PABCH＝0就可以了。由勾股差性质
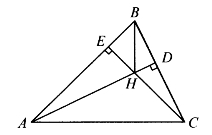
图6-29
命题得证。
[例6.5.4] 如图6-30，ABCD和APQR是两个相似的矩形，求证：BP⊥RD。
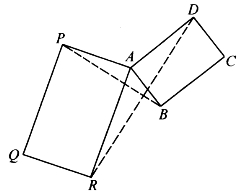
图6-30
证明：只要证明PBDPR＝0即可。由勾股差的可分性得
PBDPR＝PBDPA+PBAPR。
又因BA⊥AD，PA⊥AR，得
PBDPA＝PADPA，PBAPR＝PBAAR。
所以 PBDPR＝PADPA+PBAAR＝PPAD+PBAR
＝2AD·APcos∠DAP+2AB·ARcos∠BAR
＝2（AD·AP－AB·AR）cos∠DAP＝0。
最后一步用到∠DAP与∠BAR互补，以及两个矩形的相似性。
【注释】
[1]已故数学大师华罗庚在《1978全国中学数学竞赛题解》前言中就提到，那年命题时想出这个题目，但因没找到初等解法而作罢。
有关从数学教育到教育数学的文章
- 详细阅读
-
数学图解：分形维度长度与面积的关系详细阅读
康托尔集的豪斯多夫维度大约是0.63，科赫雪花的豪斯多夫维度大约是1.26，门格海绵看上去是介于面积和体积之间的某种概念，它的豪斯多夫维度大约是2.73。这些分形的存在模糊了各维度之间的边界。......
2023-11-22
-
数学教育：应用面积公式解题，从浅入深详细阅读
[例4.4.1]试证明在△ABC中，若∠A＝∠B，则a＝b。用面积公式代入：由AB＝AC，即得sinα＞sinβ。[例4.4.3]在△ABC中，已知a＞b，求证：∠A＞∠B。由式得a＝b，这与假设a＞b矛盾。图4-22[例4.4.4]如图4-22，设△ABC中∠A的平分线为AP，求证：。[例4.4.6]已知△ABC中的∠A和b、c两边，求∠A的角平分线长。可见在AP⊥BC时取到最大值。由AB＝CD，得sin∠APE＝sin∠DQE。......
2023-10-17
-
高等数学：曲面积分的概念与性质详细阅读
在本章第一节的质量问题中，如果把曲线改为曲面，并相应地把线密度ρ（x，y）改为面密度ρ（x，y，z），小段曲线的弧长Δsi改为小块曲面的面积ΔSi，而第i小段上面的一点（ξi，ηi）改为第i小块曲面上的一点（ξi，ηi，ζi），那么在面密度为ρ（x，y，z）连续的前提下，所求的质量M就是下列和的极限：其中λ表示n小块曲面的直径的最大值.抽去它们的具体意义，就得出对面积的曲面积分的概念.定义1 设曲......
2023-10-19
-
数学教育与教育数学：创造新体系的逻辑后盾详细阅读
前面引入的新体系，逻辑结构图示见下页。欧氏几何的公理体系不止一种。欧几里得最早提出的公理体系是不严密的，现在大家所用的是由希尔伯特改进之后的公理系统，共5组20条。近代数学中，还有基于向量空间的外尔公理体系、基于距离概念的布鲁门塞尔公理体系等。我们提出的下列公理体系，主要是为了数学教育而创设，特别是为了中学数学教育的需要。这个新公理体系，是以度量为主体的公理体系。这些点之间的关系满足以下公理。......
2023-10-17
-
高考数学：空间几何体的表面积与体积详细阅读
考点：空间几何体（2017全国I，7）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）.A.10B.12C.14D.161.如图，已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球，则平面ACD1截球O的截面面积为（）.AB.C.D.2.（......
2023-10-15
-
余祖言：黄冈教育名人详细阅读
余祖言，名淑身，字任直，又字慎之。余祖言幼承庭训，又受业于其族兄余子存与外舅李静甫，故学业早熟，年十六，中秀才，以学行兼优，拔为岁贡。光绪二十五年，余祖言至武昌，先后就读于晴川、勺庭书院。时田梓琴主持《二十世纪之支那》杂志社工作，余祖言极力参与。1906年，余祖言奉同盟会总部之命，离日归国，协理湖北分会工作，深入各界活动。楚翘之弟系留日学生，兄弟二人与余祖言、余诚交往甚密。余祖言毕生致力教育。......
2023-11-26
-
大禹勾股定理及中国数学史详细阅读
大禹治水勾股定理的称谓源于对直角三角形的认识。大禹应是世界上有史记载的第一位应用勾股定理者,其在治水实践中总结出了勾股术,用来确定两处水位的高低差。即大禹除了把勾股定理应用于治水工程之中,还把其数学原理渗透到国家的建章立制中。因此商高已漂亮证明了勾股定理。他注释了《周髀算经》,并作“勾股圆方图”,其中的“弦图”再次证明了勾股定理。......
2023-11-23
相关推荐