仅仅这样说一下，并不足以证明教育数学就有权存在，还必须说明再创造的必要性与可能性。在数学的大后方，也并非无事可做。因此，为了数学教育的目的，我们应当用“批判”的眼光审视已有的数学知识。前面，我们着重讨论平面几何、极限概念和实数理论，也正是因为它们是公认的难点。难点，给教育数学提供了课题。这是教育学与数学面临的问题，是数学教育与教育数学的共同任务。教育数学，还怕没有事做吗？......
2023-10-17
重要发现：一线串五珠，数学教育与教育数学的关系
【摘要】：如图6-14，在正△LMN内任取一点P，就有图6-14由P向MN、NL、LM分别作垂线，垂足为A、B、C，则有这里a＝MN＝NL＝LM。对于任一个不同于P的点Q，因为“斜线比垂线长”，则有比较与得这表明P是与A、B、C距离之和最小的那个点。以下的论证，就是重复式到式了。如图6-19，若A、B、C、D不共线，不妨设C在△ABD的外接圆内或圆周上。利用AC′－CC′＝AC及式得AC·BD≤BC·AD+CD·AB，其中等号仅当BC⊥A′D′
2000多年来，人们总结了许多有趣的几何题。特别是一些由名家提出，或被名家解决的流传甚广的几何名题，就如闪闪发光的珍珠，点缀着瑰丽的几何园林。下面，我们就从这些珍珠中选出5颗赏玩一番，它们都与几何不等式有关。
题1.（托勒密不等式）设A、B、C、D是平面上任意4点，求证：
AB·CD+AD·BC≥AC·BD，
且等号仅当四边形ABCD是圆内接凸四边形时成立。
题2.（费马点问题或施泰纳问题）已知平面上有A、B、C三点，求平面上这样一点P，它到三点距离之和PA+PB+PC最小。
题3.（从光行最速原理导出光折射定律）平面上A、B两点在直线l的两侧，C、D两点在直线l上。AC、BC分别和l成锐角θ1、θ2，且θ1与θ2不相邻。求证：
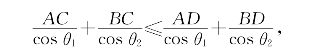
且其中等号仅当C与D重合时成立。
题4. （法格乃诺问题）已知锐角三角形ABC，求它的周长最小的内接三角形。
题5. （厄尔多斯——莫代尔不等式）设P为△ABC内或周界上的一点，P到三边的距离分别为x、y、z。求证：
PA+PB+PC≥2（x+y+z），
等号仅当△ABC为正三角形，且P为△ABC中心时才成立。
五个题目，来自相隔2000年的不同时代，来自遥距万里的不同国度，风格形式也各不相同。历代名家已有各种巧思妙解，很难想象，它们能从同一个平凡的思路入手被一一击破！本来嘛，名题之所以有名，也是因为它们各具特色，难以用统一的思路解决。
但是，我们发现确实有这么一个平凡的思路能够克敌制胜，它就是：把一块面积分成几块，几块面积之和等于原来的那一块。
下面先用这个思路解决较容易的题2。
如图6-14，在正△LMN内任取一点P，就有
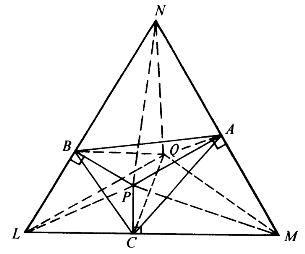
图6-14
由P向MN、NL、LM分别作垂线，垂足为A、B、C，则有
这里
a＝MN＝NL＝LM。
对于任一个不同于P的点Q，因为“斜线比垂线长”，则有
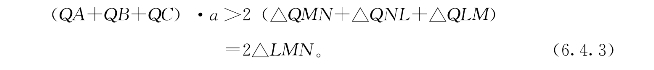
比较（6.4.2）与（6.4.3）得
这表明P是与A、B、C距离之和最小的那个点。
为了把这个结果用于题2，应当找出P点的特征。仔细观察可以看出，在四边形PANB中，因∠PAN＝∠PBN＝90°，故∠APB＝180°－∠N＝120°。同理知∠BPC＝∠CPA＝120°。于是“若△ABC内有一点P，使∠APB＝∠BPC＝∠CPA＝120°，则P使PA+PB+PC取到最小”。
证明已经有了，下面我们过A、B、C分别作PA、PB、PC的垂线，这三条垂线就构成正△LMN。以下的论证，就是重复（6.4.1）式到（6.4.4）式了。
剩下的两个小问题是：①如何找出点P？②没有这样的点P，怎么办？
找点P的方法如图6-15所示：分别以AB、AC为一边，向△ABC外作正△ABD、正△ACE，则△ABD、△ACE的外接圆的交点P（不同于A）即为所求。因为四边形PAEC、PADB是圆的内接四边形，而∠D、∠E皆为60°。
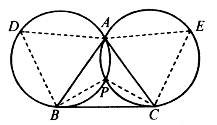
图6-15
如果∠BAC≥120°，则两圆的交点P不在△ABC内。这时，所要的点P应当与A重合。从图6-16中可以看出：如果过B、C分别作AB、AC的垂线BL、CL，BL、CL交于L，再过A作直线NM与BL、CL交于N、M，使LN＝LM，则因∠BAC≥120°得∠L≤60°，于
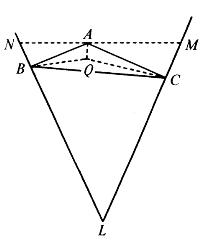
图6-16
是MN≤LN。记LN＝LM＝a，则显然有
而对任意另一点Q，则有
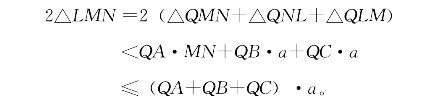
于是
这证明了A是所求的点P。
现在我们用另一种方法分割三角形，来解决题4，即求锐角三角形ABC的周长最小的内接三角形。
问题的答案是很多人知道的：周长最小的三角形是△ABC的垂足三角形。已知的最漂亮的证法是法国人小加里勃尔—马南给出的“镜像反射证法”。我们利用面积法证明是个新的思路。
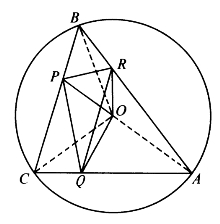
图6-17
如图6-17，设O是△ABC外接圆的圆心，又设P、Q、R分别在BC、CA、AB上，则OP、OQ、OR把△ABC分割成三个四边形OQAR、ORBP、OPCQ，则有
△ABC＝SOQAR+SORBP+SOPCQ。
设外接圆半径为r，则
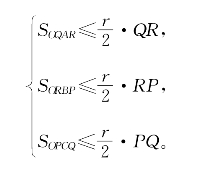
所以
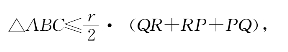
也就是
可见，内接三角形周长最小是
△ABC。而这个最小值当且仅当OA⊥QR、OB⊥RP、DC⊥PQ同时成立时才能取到。不难证明，这个条件当且仅当P、Q、R都是垂足时才能满足。
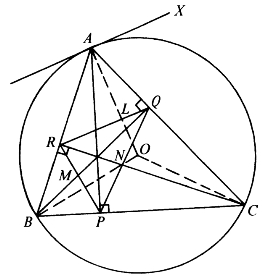
图6-18
如图6-18，如果P、Q、R都是垂足，则B、C、Q、R共圆，因而过A作切线AX后，
∠AQR＝∠ABC＝∠CAX。
于是RQ∥AX，故OA⊥RQ。同理OB⊥RP，OC⊥PQ。这说明垂足三角形周长最小。
反过来，若OA⊥RQ，则AX∥RQ。于是(www.chuimin.cn)
∠RBX＝∠CAX＝∠AQR，
R、Q、B、C共圆。同理，A、R、P、C共圆，于是
∠ACR＝∠ABQ、∠BAP＝∠BCR、∠CAP＝∠CBQ。
三式相加得
∠ACR +∠BAP +∠CAP ＝∠ABQ +∠BCR +∠CBQ 。
因为这6个角之和为180°，故
∠ACR +∠BAP +∠CAP ＝90° ，
即∠ACR+∠CAR＝90°，从而∠ARC＝90°，即CR⊥AB。同理可证AP⊥BC及BQ⊥AC。
顺便得到一个有趣的命题（这个命题曾被选为1986年全国数学竞赛的赛题）：若r是锐角三角形ABC外接圆半径，则对于BC、CA、AB上的3点P、Q、R，它们是△ABC垂足的充要条件是△ABC＝
·（QR+RP+PQ）。
在题1中，情况不同了。这里没有现成的三角形供我们分割，我们要造一个适当的三角形出来。
如图6-19，若A、B、C、D不共线，不妨设C在△ABD的外接圆内或圆周上。要证明的是
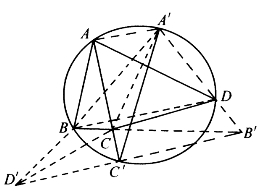
图6-19
AC·BD≤AD·BC+AB·CD，
但AD·BC和AB·CD都不能直接变成面积，所以我们要设法让AB与CD相连，AD与BC相连。
延长AC交外接圆于C′。当C点在圆周上时，C与C′重合，作直径C′A′。连接A′A、A′B、A′D，再过C′作直线C′B′∥A′A，且C′B′交A′D于B′，交A′B于D′。于是∠BAD＝∠BA′D，∠A′D′B′＝∠AA′B＝∠ADB，故△ABD与△A′B′D′相似，因而
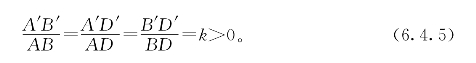
因A′C′为直径且AA′∥B′D′，故AC′⊥B′D′。于是有
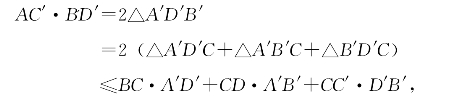
即
（AC′－CC′）·B′D′≤BC·A′D′+CD·A′B′。
利用AC′－CC′＝AC及（6.4.5）式得
AC·BD≤BC·AD+CD·AB，
其中等号仅当BC⊥A′D′且CD⊥A′B′时成立，即C与C′重合时成立。
当A、B、C、D顺次在一条直线上时，易验证等式成立。这时，我们可把直线看成是半径无穷大的圆。
题5本是当代著名数学家厄尔多斯在1935年提出的一个猜想：设P是△ABC内或周界上任一点，P到3边距离分别为x、y、z，则PA+PB+PC≥2（x+y+z）。等式仅当△ABC为正三角形，且P是△ABC的中心时才成立。
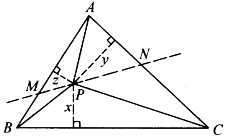
图6-20
两年后，莫代尔给出了一个证明。后来，又有人给出了较简单的证明。我们这里介绍的证法可能是最简单的。
如图6-20，过P作直线交AB于M，交AC于N，使∠AMN＝∠ACB，于是△AMN与△ACB相似。
由△AMN＝△AMP+△ANP，可得
于是若以a、b、c记△ABC的三条边，即
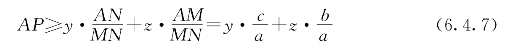
同理有
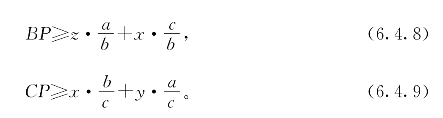
把（6.4.7）至（6.4.9）三式相加，得
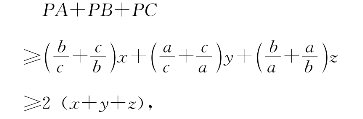
这正是所要证的不等式，且等号仅当a＝b＝c时成立。而在（6.4.6）中，等号仅当AP⊥MN时成立。这时，a＝b＝c等价于AP⊥BC，同理应有BP⊥AC及CP⊥AB。题5完全解决了。
剩下的题3与费马的“光行最速原理”有关。这个原理是：光在传播时，走的总是最节省时间的路线。
如图6-21，一束光线从A射到B，在介质分界面l上的一点C，光线会发生折射。直线AC、BC与l所夹锐角分别为θ1、θ2。光在两种介质中的速度分别为U1、U2，按折射定律：
U1∶U2＝cosθ1∶cosθ2。
如果光线经过l上另一点D到达B，用的时间是不是更多一点呢？光由A到C，需时
；由C到B，需时
。按“光行最速原里”应有
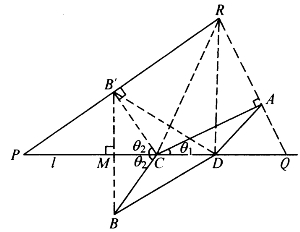
图6-21
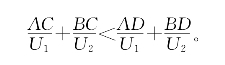
因为U1∶U2＝cosθ1∶cosθ2，所以
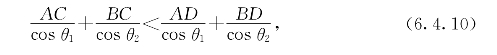
这就是题3所要证的几何不等式。
一方面，从折射定律出发，由（6.4.10）式可知光在折射时走的是最省时间的路。反之，若承认了光行最速原理，由（6.4.10）即可推导出折射定律。
国内外曾有好几位著名的数学家认为[1]，用中学里的数学知识很难证明（6.4.10）式。但是后来发现，这个不等式竟有十几种初等证法呢！
如图6-21，过B向l作垂线交l于M，延长BM至B′，使BM＝B′M，则B′C＝BC、B′D＝BD。分别过A、B′作CA、CB′之垂线，二者交于R。设RA、RB′分别交l于Q、P。于是得到
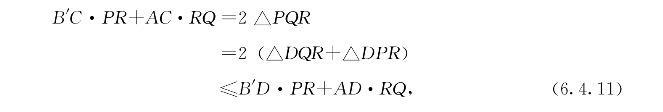
也就是
由正弦定理
PR∶RQ＝sin∠Q∶sin∠P＝cosθ1∶cosθ2，
代入（6.4.12）得
BCcosθ1+ACcosθ2≤BDcosθ1+ADcosθ2。
两端都用cosθ1·cosθ2除，即得所要证明的不等式。从（6.4.11）式可见，等式当且仅当B′D⊥PR且AD⊥RQ时成立，这只在C与D重合时才有可能。
至此，我们已经把5颗晶莹闪光的珍珠用“面积法”这条金线串起来了。
有关从数学教育到教育数学的文章
- 详细阅读
-
数学教育与教育数学：创造新体系的逻辑后盾详细阅读
前面引入的新体系，逻辑结构图示见下页。欧氏几何的公理体系不止一种。欧几里得最早提出的公理体系是不严密的，现在大家所用的是由希尔伯特改进之后的公理系统，共5组20条。近代数学中，还有基于向量空间的外尔公理体系、基于距离概念的布鲁门塞尔公理体系等。我们提出的下列公理体系，主要是为了数学教育而创设，特别是为了中学数学教育的需要。这个新公理体系，是以度量为主体的公理体系。这些点之间的关系满足以下公理。......
2023-10-17
-
更先进的数制-从数学教育到教育数学详细阅读
之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17
-
点到面推理：数学教育到教育数学详细阅读
前面的几个例子都有这个特点：利用一点邻域的性质来推出全局的性质。抓住这一点，便能建立一个统一的推理模式，使许多定理的证明简化。我们引入一个“可分命题”的概念。可分命题 设命题Q△是涉及区间△的一个判断，如果满足下面两条：若Q△成立，且△1△，则Q△成立。使用定理Q，一定要把所要证的命题设法转化成一个有关的可分命题。下面，我们用上一节的例题来说明这种推理模式的用法。推证方法同确界存在定理，用反证法。......
2023-10-17
-
8个指头强于10个指头-数学教育与教育数学详细阅读
珍贵的遗产，同时又是沉重负担。为了使珍贵的遗产传到下一代手中时更易使用和理解，人们付出了艰辛的劳动。这种文化改造工作很艰难；因为当人们发现“遗产”应当加以改造时，往往已经晚了。在这些珍贵的遗产当中，最基本的部分除语言文字外，恐怕要算数学了。看看十进制记数法吧，这可是全世界人民的共同财富。丢掉最左边的0，就是11001111。反过来，二进制下的1010110，自右向左，3个码一组，看成001，010，110，也能直译成八进制下的126。......
2023-10-17
-
面积与自然对数：从数学教育到教育数学详细阅读
为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。......
2023-10-17
-
从数学教育到教育数学：揭示华丽转换详细阅读
数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮，席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学，而不是数学本身。于是，数学教育学要靠数学提供材料。为了数学教育的需要，对数学成果进行再创造，这已不是数学教育学的任务了。这主要是数学工作者的责任，是数学的任务。......
2023-10-17
-
从数学教育到教育数学，逻辑展开与平行线定理详细阅读
命题5.4.1设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。于是，共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。命题5.4.5PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2，而l3与l1、l2相截，则内错角相等。......
2023-10-17
相关推荐