之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17
面积与自然对数：从数学教育到教育数学
【摘要】：为底的对数——自然对数。若用曲线y＝下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ＞0，有①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。至此，可以引入自然对数了。定义6.3.2对0＜x＜+∞，记＝lnx，并称函数y＝lnx为x的自然对数。从两个定义及三个推论中，立刻得到自然对数的一系列性质。
在现行高中课本中，提到了以常数e＝2.71828…为底的对数——自然对数。以后，又不加证明地介绍了极限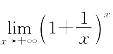
＝e，初步引进了函数ex、Inx以及其求导法则。这是很有必要的，因为ex和lnx是高等数学中极其重要的一对函数。但是，中学生学到这里，往往觉得e、ex和lnx高深莫测。
若用曲线y＝
下的面积引入自然对数lnx，则显得简单具体、直观性强，而且涉及的基础知识少，还把平面几何、解析几何与高等数学更密切地联系起来了。
定义6.3.1 在笛卡儿坐标系中，曲线y＝
（x＞0）之下x轴之上，直线x＝a和x＝b之间的面积，当b≥a＞0时，记作
，并约定（如图6-12）。
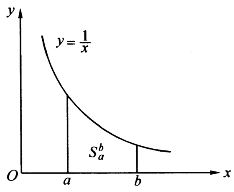
图6-12
推论6.3.1 Saa＝0。
推论6.3.2 Sba+Scb＝Sca。
任取一个正数μ，把全平面沿y轴方向作一个均匀的、比例系数为μ的“压缩”（当μ＞1时实际上是“扩张”），又沿x轴方向作比例系数为
。的“扩张”（当μ＞1时实际上是“压缩”）。这样，一个坐标为（x，y）的点A，变成了坐标为（x′，y′）＝
的点A′。由于xy＝x′y′，所以曲线y＝
的点仍变到此曲线上。
在这种变换下，任一个两边与x、y轴平行的矩形仍变成这样的矩形，而且面积不变。设P1P2P3P4是这样一个矩形，且
P1＝（x1，y1），P2＝（x2，y1），
P3＝（x2，y2），P4＝（x1，y2）。
经变换之后，矩形P1P2P3P4变为矩形P′1P′2P′3P′4，且
原来矩形的面积是｜（x2－x1）（y2－y1）｜，变换之后，矩形的面积是
没有变化。这是因为矩形的长缩小为原来的几分之一，宽就增大到原来的几倍。
利用无限细分、求和、取极限的面积计算原理可知，曲线y＝
之下的每块面积
在（x，y）→
的变换中不变。这时，点（a，0）变为
，（b，0）变为
，而
变为
，故
。
推论6.3.3 对任意λ＞0，有
①也可不用压缩变换，直接用求导方法证明sx1＝sλxλ。即令f（x）＝Sx1，g（x）＝Sλxλ，再证明f（1）＝g（1）＝0，f′（x）＝g′（x）。
这里用λ代替了
。至此，可以引入自然对数了。
定义6.3.2 对0＜x＜+∞，记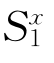
＝lnx，并称函数y＝lnx为x的自然对数。
从两个定义及三个推论中，立刻得到自然对数的一系列性质。
命题6.3.1 y＝lnx的基本性质
（1）（乘变加）ln（x1x2）＝lnx1+lnx2。
（2）（递增性）当x1＜x2时，lnx1＜lnx2。
（4）（连续性）
。
（5）（对数函数不等式）
≤ln（1+x）≤x或
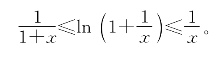
（6）（求导法则）（lnx）′＝
。
（7）（值域）当x取遍（0，+∞）时，lnx取遍全体实数。
下面列出证明这些性质的方法：
性质（1）可由定义及推论6.3.3证明。
ln（x1x2）＝
。这里关键的一步是
，这相当于推论6.3.3中取a＝1，b＝x2，而λ＝x1。由性质（1）还可知ln
＝lnx2－lnx（1只要在（1）中取
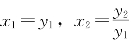，可得lny2＝ln y1+
）以及lnxn＝nlnx。
性质（2）、（3）、（4）均由定义得出：
又显然有
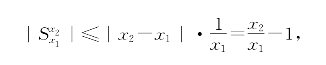
故当x1→x2时
→0，这就证明了连续性。
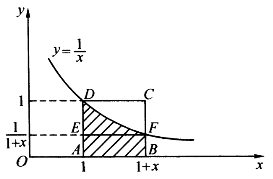
要证明性质（5），当x＞0时，参看图6-13，就一目了然了。
图中阴影部分面积是ln（1+x），小于矩形ABCD的面积1·x＝x，大于矩形ABFE的面积x·
，即不等式（5）成立。当x＜0时，不等式
可由
(www.chuimin.cn)
图6-13
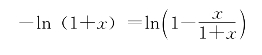
导出。
性质（6）可由性质（1）与（5）导出。按导数定义，
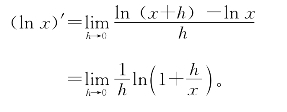
当h＞0时，由（5）得
当h＜0时，由（5）得
令h→0取极限即得
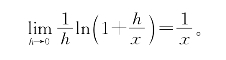
性质（7）可由连续性及lnan＝nlna推出。当a＞1时，
可见lnx取遍（－∞，+∞）的值。
由递增性与连续性知，lnx有唯一的反函数E（x），且E（x）连续递增。因为lnx定义于（0，+∞）而值域为（－∞，+∞），故E（x）定义于（－∞，+∞）而取值于（0，+∞）。又由反函数求导法则可知
（E（x））′＝E（x）。
现在引入记号E（1）＝e，我们指出，E（x）恰巧就是指数函数ex。
首先，若设y1＝lnx1，y2＝lnx2，则
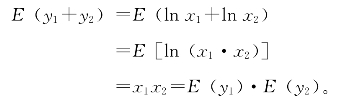
最后两步是根据反函数的定义得来的。
因为y1、y2是任意的，可得
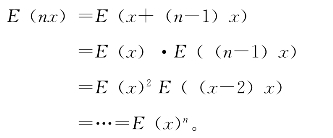
取x＝1，得E（n）＝（E（1））n＝en；又取x＝
，得E
；取x＝
，得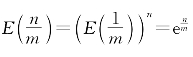
。可见对一切正分数x有E（x）＝ex，又因ln1＝0得E（0）＝1，故
E（x）E（－x）＝E（x－x）＝E（0）＝1，
即得
E（x）＝（E（－x））－1。
当x为负分数时也有
E（x）＝（E（－x））－1＝（e－x）－1＝ex。
总之，对一切有理数有E（x）＝ex。根据连续性可知E（x）＝ex对一切实数x成立。
最后，我们来看看e是什么？
由y＝lnx的基本性质（5）
取x＝
，则当A＞0时有
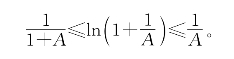
同用A乘，得
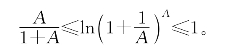
同取E（x）的值得
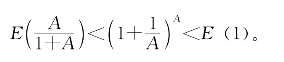
令A→+∞，两边的极限都是E（1），故
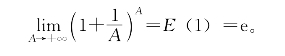
这就是目前中学课本中略去了证明的那个重要极限等式。
回顾整个推导过程，除了面积大小的比较之外，并没有用到更多的东西。这似乎比先引入e、ex，再引入lnx要直观浅显得多。这里又一次展示了面积法在数学教学中的重要作用。
微积分里有两类重要函数：三角函数与反三角函数、对数函数与指数函数，它们都可以从面积出发引出来。
有关从数学教育到教育数学的文章
- 详细阅读
-
从数学教育到教育数学：揭示华丽转换详细阅读
数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮，席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学，而不是数学本身。于是，数学教育学要靠数学提供材料。为了数学教育的需要，对数学成果进行再创造，这已不是数学教育学的任务了。这主要是数学工作者的责任，是数学的任务。......
2023-10-17
-
从数学教育到教育数学，逻辑展开与平行线定理详细阅读
命题5.4.1设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。于是，共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。命题5.4.5PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2，而l3与l1、l2相截，则内错角相等。......
2023-10-17
-
从数学教育到教育数学：连续归纳法应用详细阅读
有了连续归纳法，数学分析里的一系列涉及实数连续性和连续函数性质的定理，就可以用统一的模式来证明。以下用连续归纳法证明：这将推出每个实数都是{bn}的下界，即得矛盾。由连续归纳法，px对一切x成立。[例8.3.6]设f在[a，b]上连续，f＜0，f＞0，则至少有一个点x0∈（a，b），使f＝0。[例8.3.7]若f在[a，b]上连续，则f在[a，b]上取到最大值和最小值。......
2023-10-17
-
不使用ε-语言，讨论数列极限|从数学教育到教详细阅读
定义7.3.3设{an}是无穷数列。用“ε-语言”，不仅能够引入极限概念，还能证明与极限有关的一系列基本定理，直接计算一些具体的极限。实践证明确实有效，而且比用“ε-语言”还要简便！[例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例，说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列，{Ln}为有界数列。......
2023-10-17
-
从数学教育到教育数学，解析函数极限新方法详细阅读
既然讲数列极限可以不用“ε-语言”，那么讲函数极限也可以不用“ε-语言”，只不过用“无界不减函数”代替“无界不减数列”罢了。定义7.4.2设f是在[c，+∞）上有定义的函数。用“ε-语言”讲函数极限，常常要一条一条分别给出各种过程中的极限定义。这一套定义，将使学生在学习微积分时免受“ε-语言”之累，在定理证明和做题时用代数运算代替逻辑推理。[例7.4.1]求证：＝+∞。......
2023-10-17
-
点到面推理：数学教育到教育数学详细阅读
前面的几个例子都有这个特点：利用一点邻域的性质来推出全局的性质。抓住这一点，便能建立一个统一的推理模式，使许多定理的证明简化。我们引入一个“可分命题”的概念。可分命题 设命题Q△是涉及区间△的一个判断，如果满足下面两条：若Q△成立，且△1△，则Q△成立。使用定理Q，一定要把所要证的命题设法转化成一个有关的可分命题。下面，我们用上一节的例题来说明这种推理模式的用法。推证方法同确界存在定理，用反证法。......
2023-10-17
-
从数学教育到教育数学：深入探索一个开门见山的详细阅读
定义4.3.1 边长为1，有一个角为α的菱形的面积，叫做角α的正弦，记作sinα＝Sα。命题4.3.1在△ABC中，设BC＝a。把三角形面积公式各项同除以，立刻得到：正弦定理 在任意△ABC中，有这个定理的用处之大是众所周知的。在式中，我们取α+β＝90°，可立刻得到重要的命题。这样，为“余角的正弦”创设一个新符号将十分方便，余弦应运而生：定义4.3.2一个角α的余角的正弦，叫做α的余弦，记作cosα。......
2023-10-17
相关推荐