考点:空间几何体(2017全国I,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为().A.10B.12C.14D.161.如图,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为().AB.C.D.2.(......
2025-09-30
在平面几何教材中,“轨迹”被定义为“平面上满足一定条件的点的集合”。可是初中生接触到的轨迹,往往是一条直线、两条直线、圆、圆弧,没有充分表现出“集合”概念的丰富内涵。如果我们把面积与轨迹联系起来,分析一些与面积有关的轨迹问题,就能较丰富地体现集合概念,使集合思想更多地渗入平面几何之中。
[例6.1.1] 设A、B、C、D4点在一条直线上,试求平面上满足条件
△PAB=△PCD
的点P的轨迹。
解:有两种情形:
(1)若AB=CD,则平面上每一点都满足条件,因此所求的轨迹是全平面。
这里我们承认了共线三点也可以形成三角形,即退化的三角形。若不然,所求轨迹就是去掉了一条直线的全平面。
(2)若AB≠CD,则当P不在直线AB(或说直线CD)上时,是无法满足条件的。当P在这条直线上时,△PAB=△PCD=0。因而所求轨迹是A、B、C、D所在的直线。
[例6.1.2] 设ABCD是等腰梯形,AB、CD是梯形两腰,求平面上满足条件
△PAB=△PCD
的点P的轨迹。
解:分两种情形:
(1)若AB∥CD,所求轨迹是梯形两底中点所确定的直线(若定义梯形时排除两腰平行的情况,则此条无效)。
(2)若直线AB、CD交于O,则所求轨迹除了梯形两底中点连线之外,还包括过点O与梯形之底平行的直线。也就是说:所求轨迹是直线AB、CD交成的一对对顶角的两条角平分线。理由从下文可以看出。
[例6.1.3] 设A、B决定一条直线l1,C、D决定另一直线l2,l1与l2交于O。求平面上满足条件
△PAB=△PCD
的点P的轨迹。
解:如图6-1,在直线AB上取E、F,使O为EF的中点,且EO=FO=AB。再在直线CD上取G、H,使O为GH的中点,且GO=HO=CD。则四边形EGFH为平行四边形。设EG、GF、FH、HE4条边的中点顺次为M、S、N、R。我们断言:所求的轨迹就是直线MN和直线RS。
先证轨迹的纯粹性。注意,当线段CD在直线HG上“滑动”时,对固定的任一点P,面积△PCD是不变的。同样的,线段AB在直线EF上滑动时,△PAB也不变。于是

图6-1

当P在直线RS上时,由共边比例定理知

当P在直线MN上时,同理

这表明直线RS和直线MN上的点都在轨迹上。
再证轨迹的完备性。若Q不在直线MN或RS上,不妨设Q是∠ROE内的任一点,连OQ交RE于T,则TE<RE=HR<HT。由共边比例定理

可见Q不在轨迹上。
[例6.1.4] 设A、B、C、D都在直线l上,a是给定的正数,求平面上满足条件
△PAB+△PCD=a
的点P的轨迹。
解:有两种情形:
(1)若A与B重合,且C与D重合,则对平面上任一点P总有△PAB+△PCD=0<a,故所求轨迹是空集。
(2)若AB+CD>0,则所求轨迹显然是与直线l平行、且到l的距离为

的两条直线。
[例6.1.5] 若ABCD是平行四边形,a是给定的正数,求平面上满足条件
△PAB+△PCD=a
的点P的轨迹。
解:分三种情形:
(1)若▱ABCD面积大于2a,所求轨迹是空集。
(2)若▱ABCD面积等于2a,如图6-2(1),所求轨迹是直线AB与CD所夹的条形区域(含直线AB、CD)。
(3)若▱ABCD面积小于2a,如图6-2(2),所求轨迹是与AB平行的两条直线l1、l2。l1与l2分居于AB、CD所夹条形区域的两侧,到条形区域边界距离为

图6-2

这里d是AB到CD的距离。
轨迹(2)与(3)的证明从略。
[例6.1.6] 设ABCD是平行四边形,求平面上满足条件
△PAB+△PBC+△PCD+△PDA=a(https://www.chuimin.cn)
的点P的轨迹。这里a是一个给定的正数。
解:分三种情形:
(1)若▱ABCD面积大于a,所求轨迹是空集。
(2)若▱ABCD面积等于a,所求轨迹是平行四边形内和周界上的所有的点。
(3)若▱ABCD面积小于a,所求轨迹是如图6-3所示的包围了▱ABCD的八边形。设▱ABCD面积为S,AB到CD距离为d1,AD到BC距离为d2,则图中确定八边形的参数h1、h2如下:


图6-3
这是因为P(当P在DC外侧时)应当满足
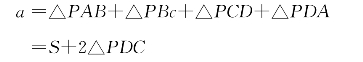
之故,详细证明从略。
[例6.1.7] 设l1、l2两直线相交于O。在l1上取两点A、B,在l2上取两点C、D。设a是任意给定的正数,求满足条件
△PAB+△PCD=a
的点P的轨迹。
解:如图6-4,在l1上取E、F,使△EDC=△FDC=a。在l2上取G、H,使△GAB=△HAB=a。显然O是EF的中点,也是GH的中点。于是,四边形EGFH为平行四边形。

图6-4
我们说:这个平行四边形的周界就是所求的轨迹。
下面先证轨迹的纯粹性。设P在▱EGFH周界上,比如在EG边上。设PG=λEG。由共边比例定理

所以

同理
![]()
(1)+(2)得△PAB+△PCD=a,纯粹性得证。
下证轨迹的完备性。设Q不在▱EGFH周界上,连QO交其周界于P,则由共边比例定理得
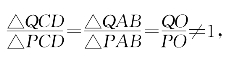
合比之,得

即Q不在轨迹上。
以上举的例子都是直线型轨迹。下面介绍一个涉及圆的轨迹。
[例6.1.8] 给了平面上两点A、B,对给定的常数k≥0,求满足条件
![]()
的点P的轨迹。
解:有多种情形:
(1)若A、B重合而k>0,轨迹由一个点A构成。
(2)若A、B重合而k=0,轨迹是全平面。
(3)若A、B不重合而k=0,轨迹是直线AB。
(4)若A、B不重合而k>![]() ,轨迹由A、B两点构成。
,轨迹由A、B两点构成。
(5)若A、B不重合而0<k≤![]() 时,将(6.1.1)式与三角形面积公式△PAB=
时,将(6.1.1)式与三角形面积公式△PAB=![]() PA·PB·sin∠APB比较,可知(6.1.1)式等价于
PA·PB·sin∠APB比较,可知(6.1.1)式等价于
sin∠APB=2k。
由此易找出所要的轨迹。
若2k=1,则∠APB=90°,所求轨迹显然是以AB为直径的圆周。
若0<2k<1,过A作AB的垂线l。以B为圆心,![]() 为半径作弧交l于M、N,再以BM、BN为直径作两个圆,这两个圆周就是所求的轨迹(如图6-5)。这时有
为半径作弧交l于M、N,再以BM、BN为直径作两个圆,这两个圆周就是所求的轨迹(如图6-5)。这时有
![]()

图6-5
详细证明从略。
以上举出的轨迹,有空集、全平面、一条直线、两条平行线、两条相交直线、带形域、平行四边形域、平行四边形周界、八边形周界、圆周、一点集、两点集共十二种类型。这样丰富多彩的轨迹作为课外活动的资料,可使学生眼界大开。它们中的许多都是简单地用一个面积等式来描述的。很难想象,一个简单的等式有如此多的变化。学生可以由这些例子得到启发,提出别的有趣的轨迹题。
例6.1.6就可以有大量的变化:把A、B、C、D4点改为三点、任意四点或更多的点,轨迹又会是什么样子呢?
相关文章

考点:空间几何体(2017全国I,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为().A.10B.12C.14D.161.如图,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为().AB.C.D.2.(......
2025-09-30

请说明理由.若矩形ABCD面积为6,求四边形BDEG的面积.(第9题)10.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称……......
2025-09-29

以上主要按机械运动及几何学的观点,论述了各种体系的几何特征。当荷载为零时,体系的反力和内力也等于零。体系可以产生和存在初内力或自内力,这是超静定结构极为重要的一个静力特性。图2-173.瞬变体系的静力特性有关瞬变体系的几何特征,已在第三节中做了比较详细的介绍,这里我们将讨论它的静力特性。......
2025-09-30

《标准(实验稿)》中“空间与图形”的公理化体系的呈现采用课程形态的公理化体系,这是较为合理的,因为作为“空间与图形”的公理化体系应该是教育形态的公理化体系。另外,《标准(实验稿)》对“空间与图形”的呈现又体现了从点到线到面再到体,即从部分到整体的展开过程。课程标准依然坚持了这种公理化体系,并且在证明方面的要求上有所加强。......
2025-09-29

文化记忆是对意义的传承,个体人生中一些重大时刻和重要阶段所穿过的衣服,如学生时代的校服、服兵役时的军装、婚礼上的礼服或婚纱、孩子满月时的衣服、成年礼上的礼服等,对个体而言都超越了单一物的记忆范畴,具有某种象征性或者明显的身份认同价值。幸运的是,有关空间和文化记忆理论的出现为人们打开这一私人空间并深入思索该空间的存在意义提供了一个很好的研究视角。......
2025-09-29

水资源和土地资源作为自然地理系统的重要组成因子,彼此之间相互联系、相互渗透、相互制约。水资源是自然界地质循环的重要动力。成土物质沿着这条“传输带”,不间断地更替着土壤的发生与消失。水资源是传输带的重要能量之一。水土资源相互依赖、制约,与人类社会经济活动相结合,构成了其动态、大系统结构特征。......
2025-09-29

卫星沿着轨道绕地球运行,地球本身也在自转,星下点轨迹在一般情况下不会再重复前一圈运行轨迹。,为一个恒星日内卫星围绕地球旋转的次数)时,其星下点在一个恒星日内可重复,称为回归轨道卫星。N为奇数时,星下点的轨迹一定有交点在赤道上,交点数为n个,如果存在不在赤道上的交点,则一定关于赤道对称分布。图4-9为T=8 h(N=3)、轨道倾角为55°时的星下点示意图,星下点轨迹交点在赤道上,交点数为3个。......
2025-09-29

通常认为外观品质与蒸煮品质有较为显著的相关性,但关系较复杂,研究结果很不一致。石春海和申宗坦在研究粕稻外观品质与其他品质性状的相关性认为,粒宽与胶稠度性状间达到显著水平,对粒宽正向选择会明显降低胶稠度。王建林等配置了籼粳杂交组合,分析了稻米外观品质和蒸煮品质的相关性,结果显示,粒长与直链淀粉含量呈显著正相关,粒形则呈极显著正相关。稻米的垩白也与蒸煮食味品质之间存在显著、极显著水平的相关性。......
2025-09-29
相关推荐