[例4.4.1]试证明在△ABC中，若∠A＝∠B，则a＝b。用面积公式代入：由AB＝AC，即得sinα＞sinβ。[例4.4.3]在△ABC中，已知a＞b，求证：∠A＞∠B。由式得a＝b，这与假设a＞b矛盾。图4-22[例4.4.4]如图4-22，设△ABC中∠A的平分线为AP，求证：。[例4.4.6]已知△ABC中的∠A和b、c两边，求∠A的角平分线长。可见在AP⊥BC时取到最大值。由AB＝CD，得sin∠APE＝sin∠DQE。......
2023-10-17
实用性与应用：张角公式在数学教育中的价值
【摘要】：下面我们将举出一些例题，它们会极有力地表明张角公式的广泛用途。由正弦定理可知代入张角公式得再利用τ＝β+γ，即得要证等式。下面举出恒等式的一个应用。[例5.6.4]设在正△ABC外接圆的上任取一点P，PA交BC于D。证明：如图5-49，∠α＝∠β＝60°，由张角公式得因为sin120°＝sin60°，即得所求。[例5.6.6]设直角三角形ABC斜边AB上的高为CD，求证：图5-51证明：如图5-51，由张角公式可得又sin（α+β）＝sin90°＝1，代入，即得所求。
在第4小节里，我们介绍过一个“张角公式”：由P发出的三条射线PA、PB、PC，使∠APC＝α，∠CPB＝β，∠APB＝α+β＜180°（如图5-46），则A、B、C3点共线的充要条件是
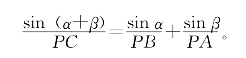
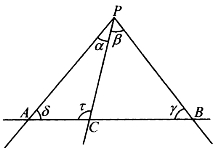
图5-46
当时就说这是一个到处用得上的解题工具，但直到现在，除了用它导出正弦加法定理之外，就再没有用过。下面我们将举出一些例题，它们会极有力地表明张角公式的广泛用途。
[例5.6.1] 设4个角α+β+γ+δ＝180°，求证：
证明：在图5-46中，取∠PAB＝δ，∠PBA＝γ，∠PCA＝τ。由正弦定理可知
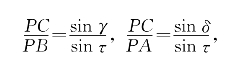
代入张角公式得
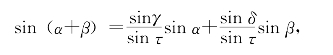
再利用τ＝β+γ，即得要证等式。
下面举出恒等式（5.6.1）的一个应用。
[例5.6.2] （托勒密定理）设四边形ABCD是圆内接四边形，求证：AC·BD＝AB·CD+AD·BC。 （5.6.2）
证明：如图5-47，设圆的直径为d，过A作圆的切线，切线与AB、AD所夹角分别记为α、δ，又令∠BAC＝β、∠CAD＝γ，于是AB＝dsinα，BC＝dsin β，CD＝dsinγ，AD＝dsinδ，AC＝dsin（α+β），BD＝dsin（γ+β）。代入（5.6.2）式，可知要证的等式等价于
d2sin（α+β）sin（β+γ）＝d2（sinα·sinγ+sinβ·sinδ），
即前例所证得的（5.6.1）式。
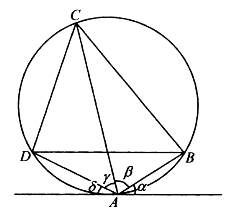
图5-47
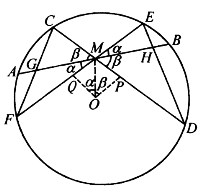
图5-48
[例5.6.3] （蝴蝶定理的又一证明）已知圆O的弦AB中点为M，过M任作两弦CD、EF，连接CF、DE分别交AB于G、H。求证：MG＝MH。
证明：如图5-48，用张角公式得
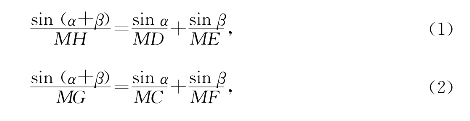
（1）－（2）得
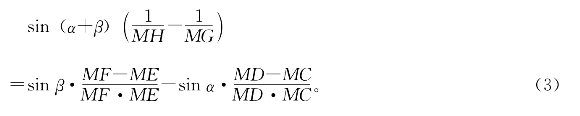
设P、Q分别是CD、EF中点，显然有
把（4）代入（3），并用MF·ME＝MD·MC，得到
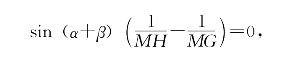
即知
MH＝MG。
[例5.6.4] 设在正△ABC外接圆的
上任取一点P，PA交BC于D。求证：
。
证明：如图5-49，∠α＝∠β＝60°，由张角公式得
因为sin120°＝sin60°，即得所求。
图5-49
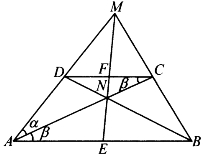
图5-50
[例5.6.5] 如图5-50，梯形ABCD的两腰AD、BC延长后交于M，两对角线相交于N，又设E、F分别是AB、CD的中点。求证：M、N、E、F在一条直线上。
证明：把命题转换一下，设直线MN分别交AB、CD于两点E、F，只要证明E、F分别是AB、CD的中点即可。
设∠BAC＝β，∠CAM＝α，AE＝e，AN＝n，AM＝m，AC＝c，AB＝b，AD＝d。由张角公式得：
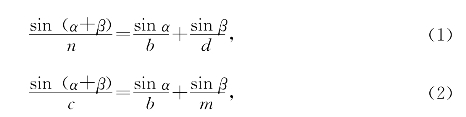
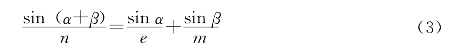
又由
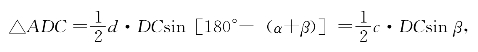
得
（1）+（2）－（3）－（4）得
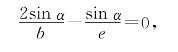
即b＝2e，亦即E为AB中点。于是
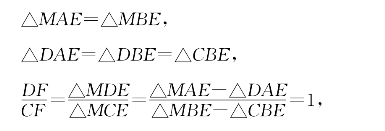
即F是DC中点。
这个命题也可以用共边比例定理来证明：
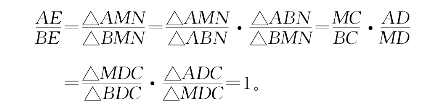
同样证明了AE＝BE。
[例5.6.6] 设直角三角形ABC斜边AB上的高为CD，求证：
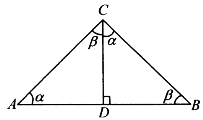
图5-51
证明：如图5-51，由张角公式可得
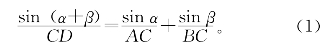
又
sin（α+β）＝sin90°＝1，
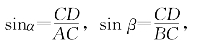
代入（1），即得所求。
[例5.6.7] 如图5-52，过∠P平分线上一点F，任作两直线AD、BC，分别与∠P的两边相交于A、D和C、B。求证：
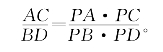(www.chuimin.cn)
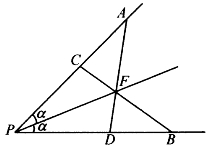
图5-52
证明：由张角公式知
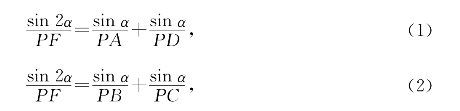
（1）－（2）得
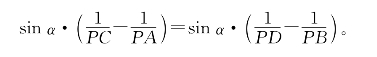
约去sinα，利用PA－PC＝AC，PB－PD＝BD，整理后即得要证等式。
[例5.6.8] 如图5-53，设PA、PB是圆的两条切线。在线段PB上取一点D，延长PA至C，使AC＝BD，连CD交AB于E。求证：CE＝DE。
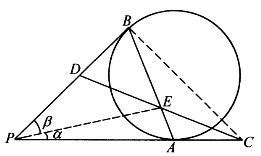
图5-53
证明：设∠APE＝α，∠BPE＝β，由张角公式得
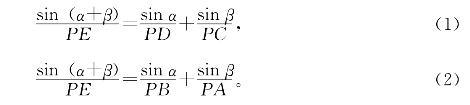
（1）－（2）得
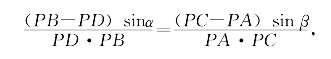
即
由BD＝AC，PA＝PB得
PCsinα＝PDsinβ，
从而
此题也可以用共边比例定理来做，方法如下：
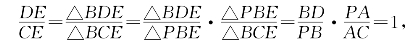
或
一般说来，使用共边比例定理证题，往往比较简捷。
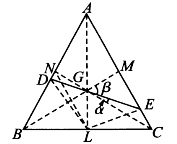
图5-54
[例5.6.9] 如图5-54，G是△ABC之重心，即3条中线的交点。过G作直线分别交AB、AC于D、E，求证：GE≤2GD。
证明：设△ABC的3条中线是AL、BM、CN，则D、E分别在线段BN、MC上。记∠CGE＝∠DGN＝α，∠MGE＝∠BGD＝β，由张角公式得
又BG＝2MG，CG＝2NG，将（1）除以（2）得
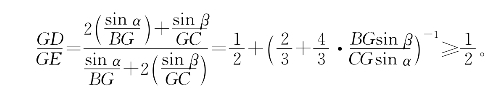
若用共边比例定理，此题做法为
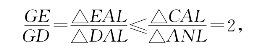
或
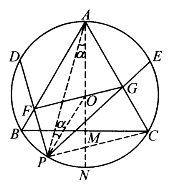
图5-55
[例5.6.10] 如图5-55，正三角形ABC内接于圆O，点D、E分别为
中点。在
上任取一点P，连接PD、PE分别交AB、AC于F、G。求证：F、G、O共线。
证明：根据张角公式，只要证明
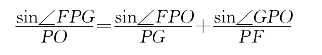
就可以了。
设∠APO＝α，圆O的直径2PO＝d，则
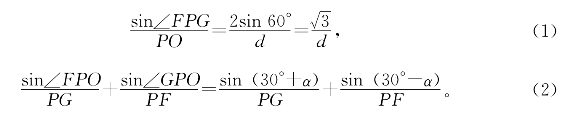
又由张角关系得
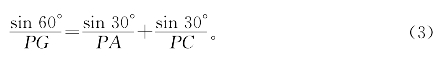
而PC＝dsin（30°+α），PA＝dcosα，代入（3）得
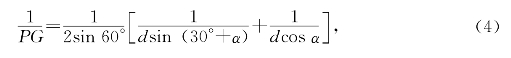
同理得
把（4）、（5）代入（2），得
由（6）与（1），即知G、D、F共线。
此题也可以从射线AF、AO、AG出发考虑。为证F、O、G共线，只要证明
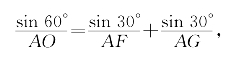
即
而
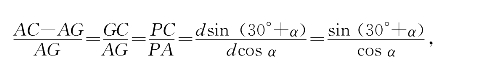
即
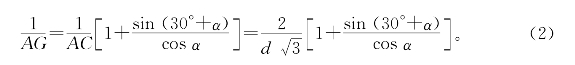
同理
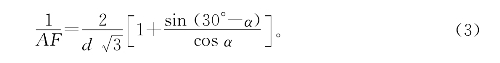
把（2）、（3）代入（1），即可验证所要证明结论。
【注释】
[1]后来作者想到一个更简单的证明：在直线AB上取一点N，使MN＝AB，则
。这个证法适用于图5-5的四种情形。
[2]当然，MN∥AB的定义如常——直线MN与直线AB无公共点。
[3]前苏联A.H.柯尔莫哥洛夫在他主编的中学几何教材中，提出过基于实数、集合、距离等概念的几何公理体系。
有关从数学教育到教育数学的文章
- 详细阅读
-
直观想象在小学数学教学中的价值详细阅读
人们对事物的了解通常是一个从感性到理性的过程，在熟悉的环境中通过直观想象抽象出实物的几何图形或几何模型，体会物体的位置关系、运动变化，提出数学问题，建立图形与数量的关系，探索解决问题的途径。例如用线段图描述复杂的数量关系，使抽象的问题直观化，进而分析解决问题。参照高中课标，直观想象的教育价值体现在学生身上即应达到的目标要求。......
2023-08-07
-
高等数学中的泰勒公式及麦克劳林公式详细阅读
=f=e0=1，f（n+1）（θx）=eθx.故f=ex的n阶麦克劳林公式为例2 求f=sinx的带有拉格朗日型余项的n阶麦克劳林公式.解 ，所以f=0，f′=1，f″=0，f=-1，f=0，…从而其中，例3 求.解 ，，所以原式.几个常用函数的麦克劳林公式：由以上带有佩亚诺型余项的麦克劳林公式，易得相应的带有拉格朗日型余项的麦克劳林公式，读者可自行写出.......
2023-11-22
-
数学教育价值—解析《数学教学论》详细阅读
数学文化的内涵的揭示，决定数学文化的教育价值的转变，影响教育工作者的教育观。所谓教育价值，是指教育对社会或个人等主体的存在或发展具有的意义或价值，数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。从我国教育现实情况来看，视数学的教育价值过于工具性，体现在数学在各种考试文化中的核心和关键学科地位。......
2023-08-13
-
泰勒公式及应用数学基础篇详细阅读
【主要内容】1.带拉格朗日型余项的泰勒公式设函数f（x）在[a，b]上具有直到n阶的连续导数，在（a，b）内具有n+1阶导数，则对x0∈[a，b]，有（x∈[a，b]）.（1）其中，余项，ξ是介于x0与x之间的实数）.设函数f（x）在（a，b）上具有直到n+1阶导数，则对x0∈（a，b），有其中，余项，ξ是介于x0与x之间的实数）.式（1）和式（2）称为f（x）按（x-x0）的幂展开的带拉格朗日型......
2023-10-27
-
高考数学应用题：导数在函数中的应用详细阅读
续表考点：导数在研究函数中的应用（2017全国I，21）已知函数f（x）=ae2x+（a-2）ex-x.（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围.1.（2017山东莱芜二模）已知函数f（x）=ex[x2+（a+1）x+2a-1].（1）当a=-1时，求函数f（x）的单调区间；（2）若关于x的不等式f（x）≤ea在[a，+∞）上有解，求实数a的取值范围；（3）若曲线y=......
2023-10-15
-
数学建模：概念、步骤及教育价值详细阅读
“数学建模是运用数学思想、方法和知识解决实际问题的过程，已经成为不同层次数学教育重要和基本的内容”，数学建模就是用数学语言描述实际现象的过程。（三）数学建模的一般步骤例1哥尼斯堡七桥问题。建立模型分析：根据题意，设y表示旅馆一天的总收入，x为与160元相比降低的房价。事实上二次函数在［0，90］之内只有一个极值点25。......
2023-08-13
-
国内数学教育中对有声思维的应用详细阅读
国内研究者对“有声思维”在数学教育中的应用研究，主要有骆开良的《论“出声思考”在初中数学教学环节中的实施》，周咏梅的《“出声思维”，激发高中生数学学习潜能》，王雪玉的硕士论文《出声思维在小数乘法中的应用研究》等。王雪玉的硕士论文《出声思维在小数乘法中的应用研究》是“有声思维”与小学数学教育相关的研究。[7]陈琴：《美国学校“有声思维”教学及启示》，载《教育科学研究》2016年第8期，第69页。......
2023-11-03
相关推荐