（一）学前儿童数学教育的总目标对周围环境中事物的数量、形状、时间和空间等感兴趣，有好奇心和求知欲，喜欢参加数学活动和游戏。（二）学前儿童数学教育各年龄阶段目标年龄阶段目标是对总目标架构下的具体化表现的阐述，表述的是对某一特定的年龄阶段进行教育所期望达到的结果。《3—6岁儿童学习与发展指南》中对幼儿数学认知领域提出以下年龄阶段目标。......
2025-09-29
数学教育与教育数学：创造新体系的逻辑后盾
【摘要】：前面引入的新体系，逻辑结构图示见下页。欧氏几何的公理体系不止一种。欧几里得最早提出的公理体系是不严密的，现在大家所用的是由希尔伯特改进之后的公理系统，共5组20条。近代数学中，还有基于向量空间的外尔公理体系、基于距离概念的布鲁门塞尔公理体系等。我们提出的下列公理体系，主要是为了数学教育而创设，特别是为了中学数学教育的需要。这个新公理体系，是以度量为主体的公理体系。这些点之间的关系满足以下公理。
前面引入的新体系，逻辑结构图示见下页。
这里，我们还少一个公理系统。
欧氏几何的公理体系不止一种。欧几里得最早提出的公理体系是不严密的，现在大家所用的是由希尔伯特改进之后的公理系统，共5组20条。后来，又有人提出过欧氏几何的其他公理体系。例如2025年，前苏联著名几何学家A.D.亚历山大洛夫在一篇文章里提出过新的几何公理系统，其特点是在公理中只有线段和点而无直线。
近代数学中，还有基于向量空间的外尔公理体系、基于距离概念的布鲁门塞尔公理体系等。
但是，所有这些公理体系，没有一个是着眼于中学数学教育而创立的[3]。我们提出的下列公理体系，主要是为了数学教育而创设，特别是为了中学数学教育的需要。它支持面积法的新体系。
这个新公理体系，是以度量为主体的公理体系。在这个系统中，所谓平面，是由一些名叫“点”的元素组成的集合。这些点之间的关系满足以下公理。
（1）（距离公理）两点A、B决定一个距离｜AB｜，｜AB｜是非负实数。｜AB｜＝｜BA｜，且｜AB｜＝0当且仅当A＝B时成立。
（2）（线段连续公理）若A、B是不同的两点，则对任给的非负实数r，有唯一的一个点P，使得下列两条件同时成立（如图5-39）。
①｜AP｜＝r。
②当r≤｜AB｜时，有｜AP｜+｜PB｜＝｜AB｜；当r＞｜AB｜时，有｜AB｜+｜BP｜＝｜AP｜。
图5-39
以下为了表达起来方便，引入线段、延长线、射线、直线等概念。
线段的定义 设A、B是任意两个点，一切满足条件｜AP｜+｜PB｜＝｜AB｜的点P组成的集合称为线段AB。（注意，线段AB和线段的长度｜AB｜在不会混淆时，都可以记作AB。）点A、B都叫做AB的端点。当A＝B时，说线段AB退化为一点（图5-39中r≤｜AB｜的情形）。
延长线的定义 设A、B是不同的两点，一切满足条件｜AB｜+｜BP｜＝｜AP｜的点P组成的集合，叫做AB（在B侧）的延长线。一切满足条件｜BA｜+｜AP｜＝｜BP｜的点P组成的集合，叫做BA（在A侧）的延长线（如图5-40）。定义中写在括号内的词可省略。
图5-40
射线的定义 设A、B是不同的两点，线段AB和AB（在B侧）的延长线的并集，叫做以A为端点沿AB方向的射线。
直线的定义 设A、B是不同的两点，AB（在B侧）的延长线、BA（在A侧）的延长线和AB的并集，叫做由AB确定的一条直线，也称为直线AB。
换言之，点P在直线AB上的充要条件是下列三式之一成立。
或者合起来说
（BA+AP－BP）（AB+BP－AP）（AP+PB－AB）＝0。
下面继续介绍我们的公理：
（3）（面积公理） 三点A、B、C决定一个面积｜△ABC｜，｜△ABC｜是一个非负实数，且｜△ABC｜＝｜△ACB｜＝｜△BAC｜＝｜△BCA｜＝｜△CAB｜＝｜△CBA｜。当A、B、C不在同一条直线上时，｜△ABC｜＞0。
（4）（非退化公理） 平面上至少有三个点A、B、C使｜△ABC｜＞0。
（5）（线性公理） 若A、B、C三点在一条直线上，AB＝λAC，P是平面上任一点（如图5-41），则｜△PAB｜＝λ｜△PAC｜。
公理（5）是我们系统中一条主要的公理，即本章开始提到的基本命题。它实际上是说：同高三角形面积之比等于底之比。但表面上，公理（5）既没有提到高，也没有提到三角形。事实上，我们只定义了｜△ABC｜，并没有定义△ABC。
图5-41
（6）平面上四点A、B、C、D，如果三对线段AB与CD、AC与BD、AD与BC中，每一对都没有异于A、B、C、D的公共点，则四个面积｜△ABC｜、｜△ABD｜、｜△ACD｜、｜△BCD｜中必有一个等于另外三个之和。例如图5－42左图中的AC、BD有异于A、B、C、D的公共点，不符合题意；而右图符合题意，故有
｜△ABC｜＝｜△ACD｜+｜△ABD｜+｜△BCD｜。
公理（6）刻画了平面的一个重要特征。有了公理（6），我们就可以定义三角形、凸四边形和凹四边形了。
图5-42
三角形的定义 对于给定的三个点A、B、C，所有满足条件
｜△PAB｜+｜△PBC｜+｜△PCA｜＝｜△ABC｜＞0
的点P组成的集合，叫做三角形ABC，记作△ABC。若上式的左端每项都不是0，则称点P是△ABC的内点；否则，叫做△ABC的边界点。平面上其他点叫做△ABC的外点。点A、B、C叫做△ABC的顶点。线段AB、BC、CA叫做△ABC的三条边。
在不至于引起混淆时，我们也用记号△ABC表示｜△ABC｜。
当｜△ABC｜＝0时，线段AB、BC、CA之并称为退化△ABC。一般所说的△ABC，均指非退化的三角形。
凸四边形的定义 若线段AC和BD有异于A、B、C、D的公共点P，则称△ABC和△ACD之并为凸四边形ABCD（或BCDA、CDAB、DABC）。AC、BD叫做凸四边形的两条对角线。AB、BC、CD、DA叫做凸四边形的四条边。
为了证明此定义的合理性，应当指出：△ABC与△ACD之并和△BDA与△BDC之并是同一个集合。这在直观上是显然的，证起来也不难：只要先把四边形分成△PAB、△PBC、△PCD、△PDA就可以了。
凹四边形的定义 若D在△ABC内部，则称△ABD和△BDC之并为凹四边形ABCD。线段AC、BD叫做凹四边形的对角线，而AB、CB、CD、DA叫做凹四边形的四条边。
（7）若P是△ABC的内点而Q是△ABC的外点，则线段PQ上必有△ABC的边界点。
下面，我们进一步引入角度这个重要度量。
（8）（角度公理） 以任一点A为公共端点的两条射线组成一个角，记作∠A，或临时指定一个记号如∠1、∠2、∠α或α、β。也可以分别在两射线上各取一点P、Q（均不同于A），记此角为∠PAQ或∠QAP。每个角对应一个非负实数α（0°≤α≤180°），叫做这个角的度数。记号∠PAQ（或∠A、∠QAP、∠1）同时用以表示它的度数，记作∠PAQ＝α。当射线AQ与AP是同一条射线时，∠PAQ＝0。当A在线段PQ上时，∠PAQ＝180。（如图5-43）。(https://www.chuimin.cn)
图5-43
（9）若∠PAQ＝180°，B是异于A的点，则有∠BAQ+∠BAP＝180°，这时称∠BAQ和∠BAP互为邻补角。若∠PAQ＜180°而且B在线段PQ上，则有∠BAQ+∠BAP＝∠QAP。并且当∠QAP＞0°时，对任意实数0≤λ≤1，在PQ上有唯一的一个点B，使∠BAP＝λ∠QAP（如图5-44）。
图5-44
（10）若∠PAQ＝∠P′A′Q′，且PA＝P′A′，QA＝Q′A′，则△PAQ＝△P′A′Q′。
最后这两条公理，把角度与线段、角度与面积联系起来了。
这10条公理是我们讨论的出发点。10条公理中的多数，如（1）、（2）、（3）、（6）、（7）、（8）、（9），都是现行教材中既不叙述、也不证明而实际上默认了的。（5）虽不显然，却是学过小学数学的孩子易于理解的。事实上，（5）刻画了欧几里得平面的特点，相当于平行公理。如果没有它，也不用适当的东西代替它，我们就只能得到非欧几何了。
一些众所周知的有关面积的性质，很容易用这些公理推证出来。例如：
命题5.5.1 若A、B、C3点共线，则有△ABC＝0。
证明：不妨设AB＝λAC，则由公理（5）得
△ABC＝λ△ACC。
CC＝2CC（＝0），故又由公理（5）得
△ACC＝2△ACC。
故△ACC＝0，即△ABC＝0。
命题5.5.2 若P在线段AB上，则对任一点Q，有
△QAB＝△QAP+△QBP。
证明：设AP＝λAB，由AP+PB＝AB，可得PB＝（1－λ）AB。由公理（5）得
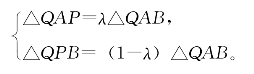
两式相加，即得所求等式。
命题5.5.3 若C在直线AB上，C异于A，则直线AC和直线AB相同。
证明：只要证明直线AC上任一点P在直线AB上，同时直线AB上任一点Q也在直线AC上就可以了。
设P在直线AC上，则△PAC＝0。设
AB＝λAC，
由公理（5）得
△PAB＝λ△PAC＝0，
再由公理（3）可知P在AB上。同理，由Q在直线AB上可推知Q在直线AC上。
这个命题的含义正是“两点决定一直线”。它在欧几里得的公理体系中是一条公理。
有一些看来很显然的事实，在目前通用的教材体系中是不好证明的，常常只能默认。下面是一个例子。
命题5.5.4 设P是△ABC的边AB上的一点，P异于A、B。又Q是PC线段上异于P、C的一点，则Q在△ABC内部。
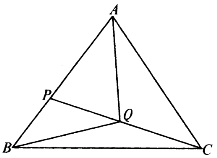
图5-45
证明：如图5-45，由命题5.5.2得
因为P不同于A、B，故△PAC、△PBC均非0。又因Q不同于P、C，故△QAC、△QAP、△QBC、△QPB均非0。由三角形定义可知Q在△ABC内。
引进了公理系统，是不是在课堂上就要把它作为平面几何学习的开端呢？大可不必。从公理系统入手讲几何，就像学骑自行车先学上车一样。骑自行车本来先要上车，但学骑车时可以先请别人扶着、爬上车学前进，学会了蹬车前进，回过头来学上车是容易的。
从历史上看，几何公理体系是在积累了大量几何知识之后诞生的。逻辑上，应是先有公理，后有丰富多彩的定理和公式。可人的认识过程恰恰相反，是先掌握了大量的定理，然后，为了彻底弄清这个定理的依据，才想到了建立公理体系。
给初中生教几何，似乎应当遵循认识的顺序，而不完全依照逻辑的顺序；也就是先带他们欣赏五光十色的几何园地，再告诉他们这个园地的基石在何处。这样，既符合认识规律，也适应年龄特征。所以，我们在给初中生讲几何时，开始不但不必列出公理，就连命题5.5.1至命题5.5.4这些显然的几何事实，也不必一板一眼地去证。其实，通常的中学几何教材也不十分强调严密性。等学生有了较多的几何知识，对几何有了感情，再回过头来进行严密化的工作是容易的。
具体地说，我们列出的公理不过是“立此存照”，表明以面积为中心的体系有自己的逻辑基础。几何教学逻辑上的出发点，明确指出的只有公理（5），其他的仅作为直观的事实应用而已。
至于这个公理系统的协调性、独立性与完备性的研究，就不属于本书的任务了。
应当提一提的是，我们提供的改革方案，是一套富有弹性的改革方案。教师们可以根据自己的见解和学生的水平，在不同层次上吸取这些资料。
至少，可以吸取这里提供的解题方法与技巧而不采纳推理体系，这是最容易采取的步骤。事实上，面积方法近年来已经受到广大中学数学教师的重视和中学生的喜爱。
进一步，可以采用这里提供的推理体系而不接受公理系统。因为我们的推理体系可以在旧的公理系统内回旋，只要集中力量，先推出三角形面积等于底乘高的一半。
更彻底的是采纳这个公理体系，或建立与此类似的公理体系。
传统的力量是强大的，任何改革都会遇到许多困难。假使新体系能被接受，也需要一个相当长的过程。
相关文章
- 详细阅读
-
从数学教育到教育数学：深入探索一个开门见山的详细阅读
定义4.3.1 边长为1，有一个角为α的菱形的面积，叫做角α的正弦，记作sinα＝Sα。命题4.3.1在△ABC中，设BC＝a。把三角形面积公式各项同除以，立刻得到：正弦定理 在任意△ABC中，有这个定理的用处之大是众所周知的。在式中，我们取α+β＝90°，可立刻得到重要的命题。这样，为“余角的正弦”创设一个新符号将十分方便，余弦应运而生：定义4.3.2一个角α的余角的正弦，叫做α的余弦，记作cosα。......
2025-09-30
-
8个指头强于10个指头-数学教育与教育数学详细阅读
珍贵的遗产，同时又是沉重负担。为了使珍贵的遗产传到下一代手中时更易使用和理解，人们付出了艰辛的劳动。这种文化改造工作很艰难；因为当人们发现“遗产”应当加以改造时，往往已经晚了。在这些珍贵的遗产当中，最基本的部分除语言文字外，恐怕要算数学了。看看十进制记数法吧，这可是全世界人民的共同财富。丢掉最左边的0，就是11001111。反过来，二进制下的1010110，自右向左，3个码一组，看成001，010，110，也能直译成八进制下的126。......
2025-09-30
-
更先进的数制-从数学教育到教育数学详细阅读
之所以说十进制并非尽善尽美，我们有更有力的理由：因为还有比十进制记数法更优越的方法。充分利用这5个指头，能造出更好的记数法来。这种记数法的好处，不仅在于少用了6，7，8，9这4个数码，更重要的是运算起来方便。比方说，3.68在新记数法里是，截尾之后得到，恰好是3.7，相当于把3.68最后的8进上去。可见，十进制记数法虽然是一份珍贵的遗产，同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2025-09-30
-
学前儿童数学教育设计与指导详细阅读
重叠法就是把两个以上物体重叠在一起进行比较。在实际生活中，随着幼儿年龄的增长，可多鼓励幼儿用目测的方式进行比较，用重叠法和并放法进行验证。（二）量的守恒教育活动的设计与指导量的守恒是指物体的大小、长短等不受物体的外形和摆放位置的变化而改变。量的守恒的教学应在幼儿认识了相应的量的基础上进行。......
2025-09-29
-
数学教育价值—解析《数学教学论》详细阅读
数学文化的内涵的揭示，决定数学文化的教育价值的转变，影响教育工作者的教育观。所谓教育价值，是指教育对社会或个人等主体的存在或发展具有的意义或价值，数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。从我国教育现实情况来看，视数学的教育价值过于工具性，体现在数学在各种考试文化中的核心和关键学科地位。......
2025-09-29
-
学前儿童数学教育环境的创设详细阅读
作为影响儿童数概念的重要因素和条件之一，幼儿园数学教育环境问题得到学前教育工作者的高度关注。区角活动的特点是支持幼儿个别化的学习方式，幼儿在操作区角材料时经常会自主突破常规思维，创新活动内容和材料，这是幼儿通过假设、想象另谋活动途径和方式，赋予活动内容和材料以新的诠释，这也是幼儿下意识的变通。......
2025-09-29
-
学前儿童数学教育：时间与货币概念教育要求详细阅读
（一）学前儿童时间概念的教育内容与要求1.小班初步理解与运用早上、中午、晚上、白天、夜晚等时间词语。（二）学前儿童货币概念的教育内容与要求1.中班初步了解货币的价值和作用。能进行简单的人民币的兑换，能进行1元与1角（或5角）的换算活动，以及10元与1元（或5元）的换算活动。能参与简单的购物活动。养成爱护人民币，节约用钱的好习惯。思考与练习常见的幼儿货币概念的教学方法有哪些？......
2025-09-29
相关推荐