从数学教育到教育数学，逻辑展开与平行线定理

在我们用众多的例题展示了共边定理与共角定理的广泛应用之后，就可以回过头来，把我们的基本工具——共边三角形与共角三角形，同欧几里得的基本工具——全等三角形与相似三角形作一个粗略的比较。

“共边三角形”与“共角三角形”，作为基本工具有什么好处呢？

其一是通用性。从统计学观点看，任给几个点连成直线，出现一对全等三角形或一对相似三角形的机会太少了，概率为0。所以想利用“全等”、“相似”来解题，就常常要挖空心思作辅助线，凑出全等三角形或相似三角形来。而作辅助线规律不好掌握，学生会觉得无章可循，非常困难。但共边三角形和共角三角形却比比皆是，因此它们的性质到处都用得上。

其二是条件和结论的对等性。要证明两条线段相等，常用的办法之一是构造一对全等三角形，使这两条线段成为它们的对应边。但要证明这两个三角形全等，却要满足3个条件。这就是说：为了得到一个等式，先要建立3个等式。这就有点不合算了。而在共边定理和共角定理中，却是从一个条件得到一个结论。这种对等性往往能简化证明的过程。

其三是基础的单纯性和表述的简明性。共边定理和共角定理，直接建立在小学生已经熟悉的三角形面积公式的一个简单推论上，学起来简单，也容易记得牢。而全等三角形和相似三角形的理论，推导过程较长，判定条件又多，在可接受方面相对较差。

但是，就直接包含的信息量而言，“共边”与“共角”两个定理，似不及“全等”与“相似”那一套东西丰富。解决某些问题，传统的方法也有它的简洁明快之处，因此作为宝贵遗产的一部分，我们应当把它继承下来而不是摒弃。

因此，我们在共边与共角定理的基础上进一步展开，同时把“全等”与“相似”理论作为辅助工具，兼容并包，会获得更丰富的信息与更多的解题工具。

在共边定理的基础上，我们已经建立了非常实用的命题。

定比分点公式　若P、Q两点在直线AB的同侧，R在线段PQ上，RP＝λPQ。则有

△RAB＝λ△QAB+（1－λ）△PAB。

这就是已经证明过的例题5.3.8。我们简单地应用定比分点公式，可得到平行与面积的关系。

命题5.4.1　设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。

这是上一小节已证明的例题5.3.9。现在，我们马上就可以推出欧几里得的“第五公设”了。但在这里，它可以不作为公理而作为定理。

欧几里得平行公理　过直线AB外一点P，有且仅有一条直线PQ平行于AB。

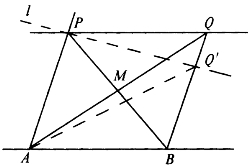
图5-25

证明：如图5-25，连接PB，设PB中点为M，连AM延长至Q，使MQ＝AM，则故PQ∥AB。这证明了过P可作AB的平行线。

△ABQ＝2△AMB＝△ABP，

再证明唯一性。如果l是过P的另一条平行线，不妨设与BQ的交点Q′在B、Q之间，这时△Q′AB＜△PAB，于是l不与AB平行。

有了这条命题，按传统方法，马上可以推出平行线的内错角、同位角、同旁内角等判定方法。鉴于目前的教科书上已不提及中间的推导过程，我们不妨在这里列出来，以方便读者学习。

命题5.4.2　两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。

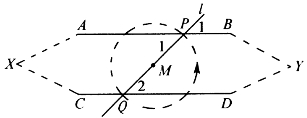
图5-26

证明：如图5-26，若直线AB与CD交于点X，取PQ中点M，图形绕M旋转180°，则P转到Q，直线AB与CD换位，而交点X变为交点Y。这样，两直线就交于两点了，故AB、CD不相交。

再利用平行线的唯一性，便可推出“若AB∥CD，则它们被另一直线所截时，其同位角相等”。这是“内角和定理”的根据。

在我们的体系中，不用旋转的概念，也能获取平行线的这条性质。我们可以从共角定理出发，开辟另一条战线。

定义5.4.1　顶角为α（0°≤α≤180°），腰长为1的等腰三角形，其面积记作S（α）。S（α）的2倍叫做α的正弦，记作sinα。

有了这个定义，我们就可以从共角定理得到三角形面积公式。

命题5.4.3　对任意三角形△ABC，有

证明：在共角定理中，取∠A′＝∠A，A′B′＝1，A′C′＝1，立刻得

△ABC＝AB·AC·△A′B′C′＝AB·AC·S（A′）

这样的正弦定义，和定义4.3.1当然是一致的。如果我们约定单位正方形面积为1，顶角为0°或180°的等腰三角形面积为0，立刻可知下列一些性质。

正弦函数的基本性质

（1）sin0°＝sin180°＝0，sin90°＝1。

（2）对0°≤α≤180°，有sinα＝sin（180°－α）。

（3）当0°≤α＜β，且α+β＜180°，有sinα＜sinβ；

当90°≤α＜β＜180°，有sinα＞sinβ。

（4）当0°≤α≤180°，0°≤β≤180°，且仅当α＝β或α+β＝180°时，才有sinα＝sinβ。

这几条性质中，（1）由定义得出，（2）的显然性由图5-27可知：

sinα＝2△ABC＝2△ACD＝sin（180°－α），

图5-27

而（3）已在例4.4.2中加以证明，（4）则是（3）的推论。有了（4），就能由面积确定角度了。

于是，共角比例定理可以完善成为

命题5.4.4　若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。反之，若这个等式成立，则∠A＝∠A′或∠A+∠A′＝180°。

从此，我们有了一个证明两角相等或两角互补的工具。

现在书归正传，继续转向对平行线的研究。

命题5.4.5　PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。

图5-28

证明：如图5-28，l交AB于M，交PQ于N。用反证法设∠NMB＝90°，而∠MNQ≠90°，过N作PQ之垂线交AB于S。在PQ上取异于N的点K，由PQ∥AB得

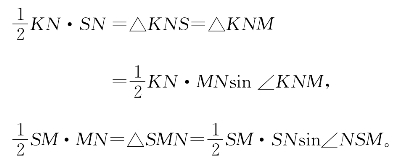
两式化简分别得到

SN＝MNsin∠KNM＜MN和MN＝SNsin∠NSM≤SN，

这二者是矛盾的。

于是立刻得到

推论5.4.1　若直线l1、l2、l3中，l1⊥l3，l2⊥l3，则l1∥l2。

推论5.4.2　平行线处处等距。

推论5.4.3　若直线l1∥l2，而l3与l1、l2相截，则内错角相等。

证明：如图5-29，不妨设l3不与l1、l2垂直，l3分别交l1、l2于A、B。过A、B作l1、l2的垂线，分别交l1、l2于P、Q。由命题5.4.5可知PA⊥PB，于是

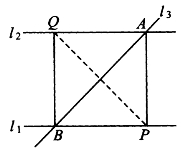
图5-29

应用命题5.4.4，可知∠PBA和∠BAQ相等或互补，因两者都是锐角，故∠PBA＝∠BAQ。

再应用平行线的唯一性，可知推论5.4.2的逆命题也真。“三线八角”的平行判定便有了。重要的副产品是

推论5.4.4　三角形内角和等于180°。

这样，我们表明了一个事实：从我们的基本命题（如图5-3）出发，确能导出内角和定理。这也并不新鲜，高斯早已指出：“只要承认平面上有面积任意大的三角形，就能导出平行公理。”我们的基本命题当然蕴涵了“有任意大的三角形”这一事实。

当然，在实际教学中不一定采用这种迂回的方法。从平行线的唯一性着手，用传统方法推出内角和定理是可取的。

有了以上的准备，再向前，我们便可以像定义4.3.2那样，导出正弦定理、正弦加法定理、余弦定义、余弦定理以及三角形全等或相似的判定定理。略有不同的是，我们这里建议再添加一条有用的命题——又一个到处用得上的解题工具。

张角公式　由P发出的3条射线PA、PB、PC，使∠APC＝α，∠CPB＝β，∠APB＝α+β＜180°，则A、B、C3点在一条直线上的充分必要条件是

证明：这个命题的证明，用的是典型的面积方法。

如图5-30，如果A、B、C共线，有

用三角形面积公式，可得

图5-30

两边同除以PA·PB·PC，即得所要的（5.4.1）式。

反过来，若（5.4.1）式成立，两边同乘PA·PB·PC即得（5.4.2）式，这表明

△ABC＝｜△PAB－△Ⅰ－△Ⅱ｜＝0，

也就是说A、B、C共线。

在图5-30中，取PC⊥AB，由张角公式立刻导出正弦加法定理。取PB⊥AB，并设α+β＝x，β＝y，则α＝x－y，则由张角公式可推出正弦减法定理。

张角公式的更多应用，将在下一小节专门加以介绍。现在，我们花不多的篇幅来谈谈圆。

对圆的研究，是平面几何逻辑展开过程中的一个高潮。有了圆，几何的应用才更加广泛，几何题目也更加丰富多彩。

传统教材中，有关圆的章节出现得较晚。这不仅是由简入繁的自然趋势，也是逻辑的需要。因为研究圆的性质要用到全等三角形和相似三角形（例如弦切割定理的证明，便要用到相似三角形）。

我们却不必如此。有了共角比例定理、共边比例定理和三角形内角和定理，便能直接进入这个丰富多彩的领域了。这又体现出放射型逻辑结构的特色。

关于圆，有许多的定理。哪个是最重要的交通枢纽呢？这是我们首先要解决的问题。

我们认为，“同弧上的圆周角相等”，即所谓的“圆周角定理”，在重要性上首屈一指。因为

（1）统计表明，在解决几何问题时它被使用的频率最高。

（2）从逻辑上讲，它完全刻画了圆的性质。由它可以毫不费力地推出其他有关圆的定理。

（3）它本身不容易被其他已知的定理所代替。（例如“垂直于弦的直径平分此弦”这条定理，就容易被“等腰三角形底边上的高与中线重合”所代替。）

于是，引入圆的定义之后，先要建立圆周角定理，为此需要两条定理：一条是“三角形内角和为180°”，另一条是“等腰三角形两底角相等”。前者我们已经证明，后者可由正弦定理导出，也可以直接证明。

命题5.4.6　等腰三角形两底角相等。

证明：设△ABC中AB＝AC，则

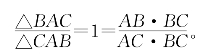
由共角比例定理的完善形式（命题5.4.4），可知∠B＝∠C或∠B+∠C＝180°，但后者不可能。

当然，也可以用余弦定理或全等三角形来做，但逻辑路线要长一些。

圆周角定理就不在这里推证了。圆周角定理的一系列推论，可分为3类：

第一类涉及与圆有关的角的度量，例如圆内接四边形对角互补、平行弦所夹两弧相等、弦切角定理、圆内角与圆外角定理等。

第二类涉及与圆有关的线段之间的关系。主要是：

圆幂定理 过点P的直线交圆于A、B，圆心为O，半径为r，则有

PA·PB＝｜OP2－r2｜。

圆幂定理的另一形式是

弦切割定理　过P点作直线交圆于A、B，又作直线交圆于C、D则

关于P在圆内的情形，我们已作为例题（例5.3.21）在前一小节给出。其实，我们可以用共角定理，对P在圆内、圆外的情形统一证明。如图5-31，不论哪种情形，在△APC与△DBP中，总有∠A＝∠D，∠B＝∠C，由共角定理可得

图5-31

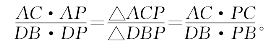
两端约去，即得所要的（5.4.3）式。这种证法并不排除A与B（或C与D）重合的情形。

这里用共角定理代替相似三角形，不仅简化了整体的逻辑结构，在细节上也省去了寻找相似三角形对应边的麻烦。

第三类涉及有关圆的线段与角之间的关系，主要是

弦长公式　若圆O的直径为d，弦BC所对的圆周角为∠BAC＝A，则有BC＝dsinA。

证明：如图5-32，过B作圆O的直径BD，则∠A与∠D相等或互补（当A在A′位置时），于是(www.chuimin.cn)

图5-32

两端约去CD，即得

BC＝BDsinA。

对于BD＝1的情形，弦长BC＝sinA。这个等式给“正弦”这个名词以生动的解释。

至此，我们都还没提到过切线。其实，关于切线的一些性质，可以作为圆周角定理、圆幂定理和弦长公式的推论。例如：弦切角定理是圆周角定理的特例；圆幂定理中当A与B重合、且C与D重合时，便成了“自圆外一点所作的两切线等长”。

不过，我们倒可以借计算切线长度的机会，引入另一个重要的三角函数——正切。

如图5-33，在直径为d的圆中有弦AB，过A、B分别作圆的切线相交于D，记AD＝BD＝l，∠DAB＝∠DBA＝∠ACB＝α，则AB＝dsinα。由

即

l·2sinα·cosα＝d·sinα·sinα，

可得

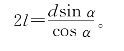
图5-33

在上式中出现的式子是十分有用的，我们给它一个记号tanα，称为正切。

命题5.4.7 比值叫做角α的正切，记号是

正切的倒数叫做余切，记号是

记号sinα、cosα、tanα、cotα的引入，可以简化几何学中推理的表述，但不改变推理的实质。有关三角函数的一切推理，总可以归结为关于正弦的推理。而正弦，不过是一块特定面积的代号。这说明解几何题的三角法，总可以还原为“纯”几何法，特别是还原为面积法。

有了正切之后，我们还可以从图5-33中发现一个有趣的事实。

命题5.4.8　在直径为d的圆中有：

圆周角α所对的弦长＝d×α的正弦。

圆周角α所对的弧长＝d×α的弧度。

圆周角α所对的切折线长＝d×α的正切。这里，“切折线长”即图5-33中AD+DB＝2l。

关于正切与余切的性质和有关公式以及解三角形的正切定理，这里不赘述。

利用弦长和切折线长的计算公式，容易得到

命题5.4.9 直径为d的圆中，外切正n边形的周长Ln和面积Sn分别为

而内接正n边形周长ln和面积sn分别为

于是立刻知道

命题5.4.10　设直径为d的圆面积为Sd，则当n≥3时

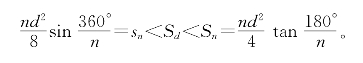
若以r＝d记半径，S（r）记半径为r的圆的面积，则有

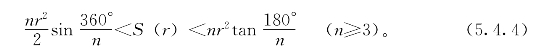
于是，单位圆面积S（1）满足不等式

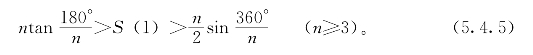
把（5.4.4）式和（5.4.5）式相比，得到

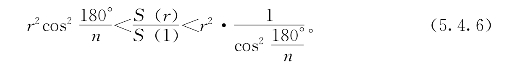
我们由此不等式来推出。用r2除（5.4.6）式，再减去1可得：

也就是

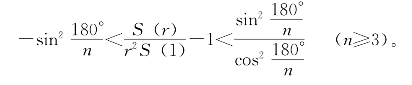
记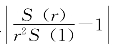＝d，则

当n≥3时，，故

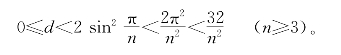
用反证法。若d≠0，取n＝表示x的整数部分）得

即d＜d，矛盾。这说明d＝0，也就是

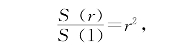
即

命题5.4.11 圆面积与半径的平方成正比。

约定一个记号π＝S（1），就得到了圆面积公式

S（r）＝πr2。

这个公式是通过严格推理得到的，甚至可以说没有借助极限概念。

至于π的计算，可以利用（5.4.6）式得

这表明，当n足够大时，nsin可以任意接近π，即

圆的周长是多少？这涉及曲线长度的定义问题，通常我们把曲线长定义为折线长的极限。这种定义方法有个缺点：不能向高维推广，不能类似地定义球的表面积。

我们主张从面积出发定义曲线长度。具体的方法是先把线“扩大”，变成一条宽度为2δ的带子。设带子面积为Fδ，再用下列极限定义曲线的长度l（如图5-34）：

图5-34

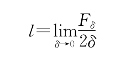
这样定义的好处是：自然地把曲线长度和面积联系起来，而且可以推广到用体积定义空间曲面面积。

按我们的定义，圆周长很容易计算：把半径为r的圆周先扩大成一个圆环，圆环外半径为r+δ，内半径为r－δ，宽度为2δ，面积

Fδ＝π（r+δ）2－π（r－δ）2＝4πδ。

按定义可求出圆周长为

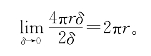
类似地，如果先把一个球的表面加厚成一个厚度为2δ的球壳体，把壳体体积Uδ除以2δ，让δ→0取极限，就能求出球面积。

至此，我们已经描绘出改建后几何园地交通系统的鸟瞰图。为了给来几何园地旅游观光的人提供方便，这里列出3套方法，可以帮助他们解决各式各样的问题。

第一套：面积方法。所用的工具是共边定理、共角定理、张角公式和三角形面积公式。这是我们的基本方法。

第二套：三角方法。用正弦定理、余弦定理、正弦和余弦的加减法定理及一些三角恒等式。

第三套：全等与相似法，即古典欧氏方法。

这3套方法，还都要用到关于平行线的一些命题以及三角形内角和定理、圆周角定理等。

在传统的欧氏方法中，还引入了一些用起来颇为方便的辅助工具。例如：平行四边形对角线互相平分，三角形的中位线定理、平行截割定理等。这些命题都能直接由面积关系导出，下面就举例证明。

[例5.4.1]　试证明：平行四边形的对角线互相平分。反之，对角线互相平分的四边形是平行四边形。

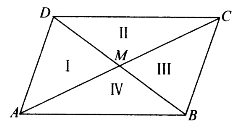
图5-35

证明：如图5-35，若AB∥CD，BC∥AD，则

△ABD＝△ABC＝△BDC。

由共边定理得

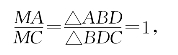
即

MA＝MC。

同理，　MB＝MD。

反之，若M同为BD、AC之中点，则

△Ⅰ＝△Ⅱ＝△Ⅲ＝△Ⅳ，

从而△ABD＝△ABC，故AB∥nc，同理AD∥BC。

这比通常用全等三角形证明要简便。

[例5.4.2]　如图5-36，直线l1、l2、l3互相平行，直线m、n分别交l1、l2、l3于A1、A2、A3和B1、B2、B3。求证：。

图5-36

证明：。

这就是所谓的“平行截割定理”，通常要在作了不少准备之后才得到它，由此可见面积法的简便。

图5-37

[例5.4.3]　（三角形的中位线定理）三角形两边中点连线平行于第三边，且等于第三边的一半。

证明：如图5-37，M、N分别是AB、AC中点，则

故MN∥BC。于是∠BNM＝∠NBC，由共角定理得

证明中最后一步也可用

解出BC＝2MN。

[例5.4.4]　（共角定理的推广）如图5-38，∠ABC与∠XYZ相等或互补。P在直线AB上且不同于A，Q在直线XY上且不同于X。求证：。

证明：不妨设B、C、X、Y共线，则

图5-38