汪曾祺的两个年代及其他一、《邂逅集》光芒难掩祖籍安徽，但出生于江苏高邮，作品也多以高邮为背景的汪曾祺，青年时代就读于抗战时期最高学府“西南联大”中国文学系，亲聆梅贻琦、刘文典、杨振声、朱自清、罗常培、冯友兰、闻一多、金岳霖、吴宓、唐兰等名师教诲①，小说创作更得沈从文悉心指导，和略早成名的穆旦及另外三位后来所谓“九叶诗人”一样，是“联大”八年在文学创作上结出的硕果。......
2024-01-11
两个定理的广泛应用及其成果
【摘要】：图5-7[例5.3.1]如图5-7，四边形ABCD的对角线AC、BD交于M。[例5.3.2]如图5-8，△ABC的两中线AD、BE交于M，求证：AM＝2MD。求证：图5-9证明：由共边定理[例5.3.4]在例题5.3.3条件下，求证：证明：由共边定理三式相乘，即得[例5.3.5]如图5-10，在△ABC的两边AB、AC上分别取两点P、Q。[例5.3.7]如图5-12，在△ABC的3边上分别取3点D、E、F，使BD＝λCD，CE＝μAE，AF＝ρBF。
表面上看，共边定理与共角定理过于平凡，很难想象它们有多大的用处。因此，在逻辑上继续向前发展之前，有必要用解题实例来表明它们的非凡功效。下面所举例题的解法，很多是仅仅用到这两条定理，还有一些会辅以其他简单的几何命题，例如三角形内角和定理、圆周角定理。晚些时候我们还会看到：三角形内角和定理可由共边定理与共角定理导出；而圆周角定理，则是圆的定义和内角和定理的推论。
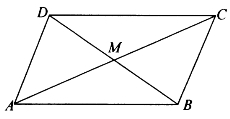
图5-7
[例5.3.1] 如图5-7，四边形ABCD的对角线AC、BD交于M。已知△ABC＝△ADC，△ABD＝△CBD，求证：M是AC、BD的中点，且△MAB＝△MBC＝△MCD＝△MDA。
证明：用共边定理及题设
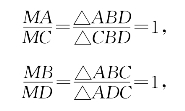
这就证明了AC与BD相互平分。再用共边定理得
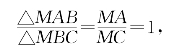
即△MAB＝△MBC。其余可类似证明。
这里，实际上已证明了“平行四边形对角线互相平分”。
[例5.3.2] 如图5-8，△ABC的两中线AD、BE交于M，求证：AM＝2MD。
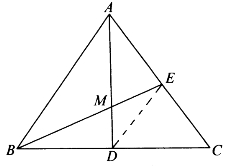
图5-8
证明：由共边定理及题设条件可知
即得要证等式。
这实际上证明了“三角形三中线交于一点”。这种证法既简单，需要的预备知识又少。
[例5.3.3] 如图5-9，在△ABC内任取一点P，连接AP、BP、CP并延长，分别交对边于D、E、F。求证：
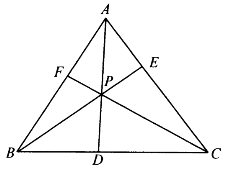
图5-9
证明：由共边定理
[例5.3.4] 在例题5.3.3条件下，求证：
证明：由共边定理
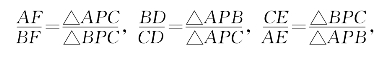
三式相乘，即得
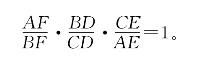
[例5.3.5] 如图5-10，在△ABC的两边AB、AC上分别取两点P、Q。已知
，设PC与BQ交于M，求
的值。
解：由共边定理，
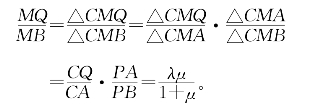
若不用共边定理，此题就颇为棘手。
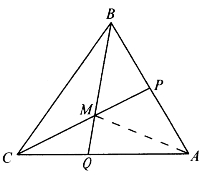
图5-10
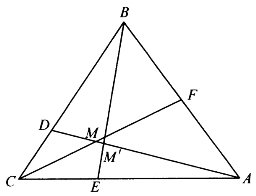
图5-11
[例5.3.6] 如图5-11，在△ABC的3边BC、CA、AB上，分别取3点D、E、F。已知
，求证：直线AD、BE、CF交于一点。
证明：设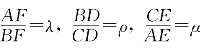
。CF与BE交于M，AD与BE交于M′，由例题5.3.5的结论可知
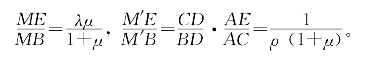
由题设λμρ＝1知λμ＝
，于是
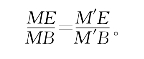
可见M与M′重合，即三线共点。
[例5.3.7] 如图5-12，在△ABC的3边上分别取3点D、E、F，使BD＝λCD，CE＝μAE，AF＝ρBF。连接AD、BE、CF，分别交于P、Q、R。求△PQR的面积。
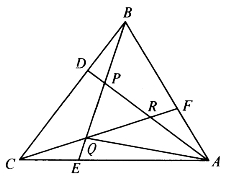
图5-12
解：设△ABC＝S，由
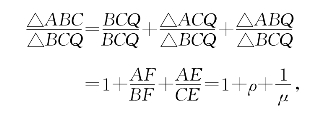
可得
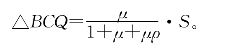
同理
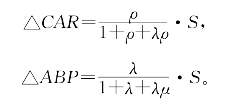
于是可以求得
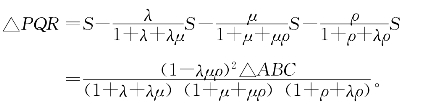
这个题目的一种特殊情况颇为有趣，当D、E、F是3边的3等分点，即λ＝μ＝ρ＝2（或
）时，△PQR恰为△ABC的
。
[例5.3.8] 如图5-13，若P、Q两点在直线AB的同侧（即线段不与直线AB相交），R在线段PQ上，PR＝λPQ，试证明：
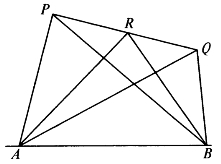
图5-13
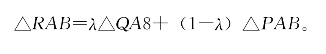
证明：设四边形PQBA面积为S，则
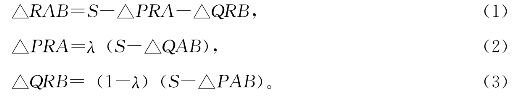
把（2）、（3）代入（1）得
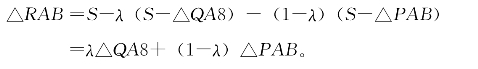
例题5.3.8又是一个很有用的命题，它可立刻推出
[例5.3.9] 设线段MN不与直线AB相交，则MN∥AB的充分必要条件是△MAB＝△NAB。[2]
证明：不妨设△MAB≥△MAB。
充分性：用反证法。设MN与AB不平行，MN延长后交AB于L（如图5-14）。
图5-14
由共边定理，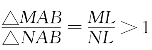
，与△MAB＝△MAB矛盾，这证明了MN∥AB。
必要性：由假设△MAB≥△NAB，下证△MAB＞△NAB不可能。因为若△MAB＞△MAB，则直线MN与AB必相交。事实上，对于MN延长线上任一点P，记λ＝
，由例5.3.8可知
△NAB＝λ△PAB+（1－λ）△MAB。
取λ＝1－
（因△NAB＜△MAB，故这是可能的）代入上式，可得△PAB＝0，即直线AB与MN交于P。这与AB∥MN矛盾，所以△MAB＞△NAB不可能，即△MAB＝△NAB。
[例5.3.10] 如图5-15，ABCD为凸四边形，在AB、BC、CD、DA边上顺次取F、G、H、E，使
＝λ，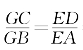
＝μ，GE与FH交于P。求证：
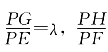＝μ。
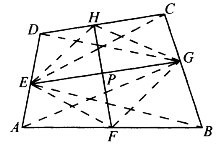
图5-15
证明：
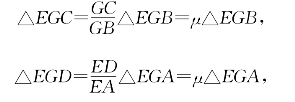
于是由例题5.3.8得：
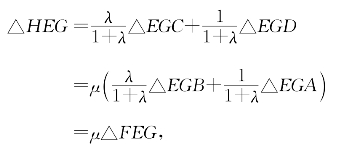
即可由共边定理推得
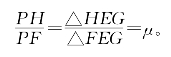
同理可证
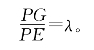
[例5.3.11] 如图5-16，在△ABC的两边AB、AC上分别取两点R、Q，直线RQ交BC的延长线于P。求证：
证明：由共边定理知
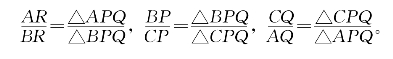
三式连乘，即得所要证明的结论。
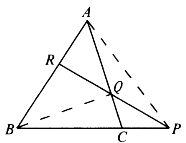
图5-16
图5-17
[例5.3.12] 如图5-17，凸四边形ABCD的两边AB、DC延长后交于L，CB、DA延长后交于K。对角线AC、BD的延长线分别交直线KL于G、F。求证：LF∶KF＝LG∶KG。
证明：由共边定理得
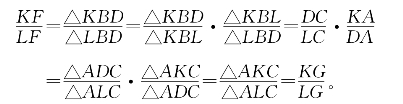
上面所举的例子都属于共边定理的应用。从下面的例题中我们可以看出，共角定理在解题过程中表现也不逊色。(www.chuimin.cn)
[例5.3.13] △ABC中∠B＝∠C，求证：AB＝AC。
证明：因△BAC与△CBA为共角三角形，故
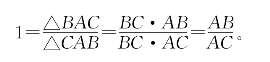
这个证法妙在把同一个三角形看成两个！这是此命题所用预备知识最少的简单证法。
[例5.3.14] 在△ABC和△A′B′C′中，∠A＝∠A′，∠B＝∠B′，求证：
。
证明：由内角和定理得∠C＝∠C′，再用共角定理得
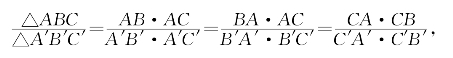
约简后即得所要证明的等式。
项武义教授在《几何学的源起与发展》一书中称上列命题为“相似形基本定理”，用若干页的篇幅阐述了这一定理的传统证法，而我们用面积方法，随便就得到了它！
[例5.3.15] 设AD是△ABC中∠A的平分线，求证：
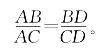
证明：因为△ADC和△ADB是共角三角形，故
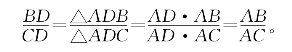
[例5.3.16] 如图5-18，在△ABC的AB和AC边上分别取点D、E，使AD＝AE。又设M是BC的中点，AM与DE交于N。求证：
。
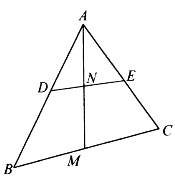
图5-18
证明：由共角定理
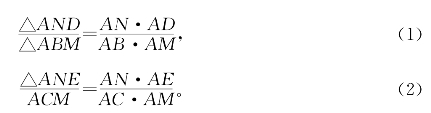
（1）÷（2），并注意到BM＝MC，AD＝AE，△ACM＝△ABM得
此题也可用共边定理来做：
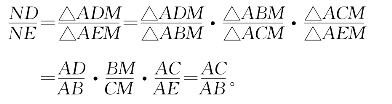
[例5.3.17] 如图5-19，自P点作四条射线PA、PB、PC、PD，使A、B、C、D在直线l1上，而直线l2与这四条射线顺次交于A′、B′、C′、D′。求证：
。
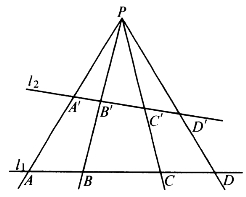
图5-19
证明：由共角定理
重排（1）的左端得
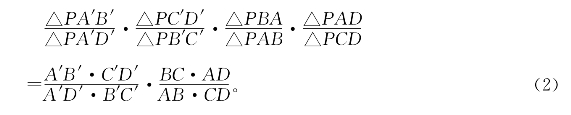
比较（1）与（2）得
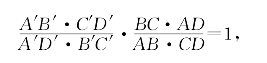
即得要证等式。
[例5.3.18] 如图5-20，在△ABC的边AB、BC、CA上分别取M、K、L。求证：△AML、△BMK、△CKL中至少有一个面积不大于
△ABC。
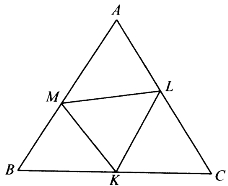
图5-20
证明：设AM＝λAB，BK＝μBC，CL＝ρCA，则BM＝（1－λ）AB，CK＝（1－μ）BC，AL＝（1－ρ）AC。
由共角定理
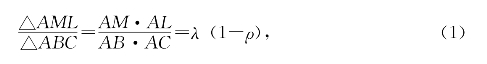
类似地
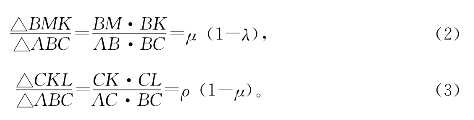
（1）×（2）×（3）得
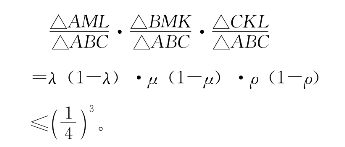
这个结论的推导是简单的，根据
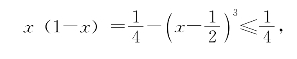
便知左端3个因式中至少有一个不大于
。
[例5.3.19] 如图5-21，设AM是△ABC在BC边上的中线，任做一条直线分别交AB、AC、AM于P、Q、N。求证：
成等差数列。
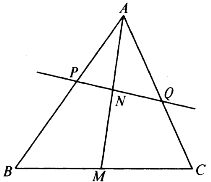
图5-21
证明：用共角定理
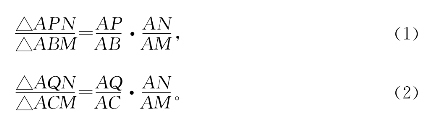
（1）+（2），并注意到
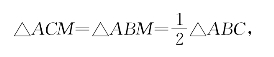
得
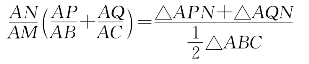
由（3）解出
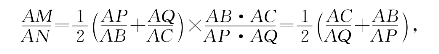
这和要证的结论等价。
[例5.3.20] 如图5-22，在凸四边形ABCD中，已知AB＝CD，E、F分别是AD、BC的中点。延长BA、CD，分别交EF的延长线于P、Q。求证：PA＝QD。
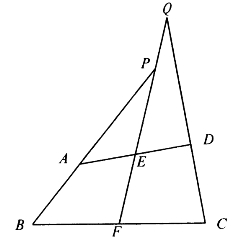
图5-22
证明：根据共角定理可得下列等式：
（1）×（2）×（3）×（4）得
记l＝AB＝CD，由（5）得
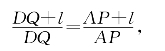
化简即得PA＝QD。
此题用共边定理解法如下：
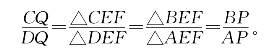
此即上列（5）式，由它可得BP＝CQ（用AB＝CD）。
[例5.3.21] 如图5-23，设圆内两弦AB、CD交于P，求证：PA·PB＝PC·PD。
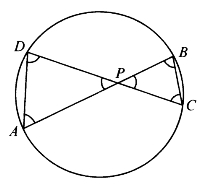
图5-23
证明：用共角定理
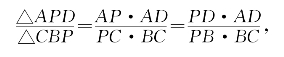
约简后即得
，亦即PA·PB＝PC·PD。
当然，这个命题也可用相似三角形来证。但用共角三角形证明，不仅减少了中间推理（建立相似三角形判定法），而且避免了辨别相似三角形对应边的麻烦。
[例5.3.22] （蝴蝶定理）如图5-24，设圆内的弦AB的中点为M，过M任作两弦CD、EF。连CE、DF，分别交AB于G、H。求证：MG＝MH。
证明：把图中所标出的4个三角形循环相比、连乘，再用共角定理及例5.3.21的结论：
图5-24
设MA＝MB＝a，MH＝x，MG＝y，则GA＝a－y，GB＝a+y，HB＝ax，HA＝a+x，则（1）式可改写成
化简（2）式，得a2x2＝a2y2，即x＝y，也就是MG＝MH。
蝴蝶定理的另一种面积证法更为直接：
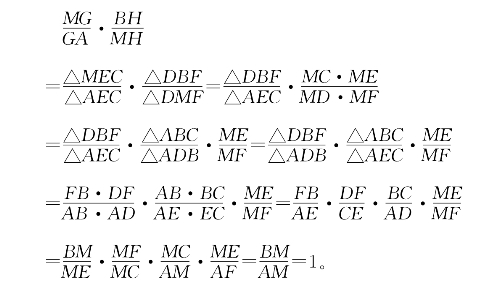
可见
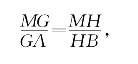
即
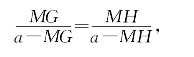
从而得到
MG＝MH。
蝴蝶定理是初等几何著名难题之一，利用共角定理证明，不仅简单明了，还不用作辅助线。这一证法把共角定理的作用发挥得淋漓尽致，充分体现了面积法的攻坚能力。
有关从数学教育到教育数学的文章
- 详细阅读
- 详细阅读
-
利用路西定理比较两个函数的零点个数详细阅读
利用路西(Rouche)定理,我们能对两个函数的零点的个数进行比较.设函数f(z)和g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C上有|f(z)| ＞0,|f(z) + g(z)| ≥|f(z)| - |g(z)| ＞0.从而在C上f(z)和f(z)+g(z)都不等于零.又设N和N′分别为函数f(z)与f(z)+g(z)在C 的内部的零点个数.由于这两个函数......
2023-10-30
-
拉氏变换定理存在-复变函数及其应用详细阅读
可以看出,拉式变换存在的条件要比傅氏变换存在的条件弱得多,但是对一个函数作拉氏变换也要具备一定的条件.对f提什么要求才能使f与指数衰减函数e-αt 的乘积在无穷区间上绝对可积？实数α=Re=Re应该取多大呢？......
2023-10-30
-
金属装饰材料及其在建筑领域的广泛应用详细阅读
金属装饰材料分为黑色金属和有色金属两大类。现代金属装饰材料用于建筑物中更是多种多样、丰富多彩。这是因为金属装饰材料具有独特的光泽和颜色作为建筑装饰材料，金属庄重华贵，经久耐用均优于其他各类建筑装饰材料。目前，随着炼铝技术的提高，铝合金已成为一种被广泛应用的金属装饰材料。铝镁锰板铝镁锰板是将铝元素、镁元素、锰元素三者按一定比例通过热轧而成的一种合金材料，是一种极具性价比的屋面、外墙材料。......
2023-10-10
-
柯西积分定理在复变函数应用中的成果详细阅读
由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式在D内恒成立.对于式右端的两个曲线积分,上述条件等式应当分别......
2023-10-30
-
毕达哥拉斯定理的发现和证明，以及其背后的故事详细阅读
据传毕达哥拉斯学派为庆祝该定理的发现曾宰杀百牛祭祀缪斯女神,但这与该学派所奉行的素食主义相悖。后人对毕达哥拉斯发现和证明勾股定理有各种猜测。图3.2.14毕达哥拉斯定理图3.2.15毕达哥拉斯定理的证明一般认为,毕达哥拉斯采用了剖分方法来证明定理。因而就有化简后则得到毕达哥拉斯定理。《几何原本》中的毕达哥拉斯定理图3.2.16毕达哥拉斯纪念碑3.2.17《几何原本》命题473.2.18希腊1955 年邮票毕达哥拉斯定理是《几何原本》第一卷命题47。......
2023-11-23
-
毕达哥拉斯定理的发现与世界各地的数学成果详细阅读
与人类文明的其他重要成就一样，毕达哥拉斯定理的发现不是某个人在某个时刻的灵光闪现，不同的国家和地区的人们在不同的时期，各自独立地得到这一发现.我国现存最早的有关天文学和数学的著作是《周髀算经》，成书年代大概在公元前2世纪，而书中的内容当然还要早.据记载，商高在回答周公关于数学计算的问题时答曰：“……故折矩，以为勾广三，股修四，径隅五……”......
2023-11-19
相关推荐