请选择其中之一说明理由.(第6题)......
2025-09-29
数学的心脏是问题,学了数学,就要能解题。
“工欲善其事,必先利其器”,要想学会解题,就要先掌握解题的工具。
平面几何图形的基本单元是三角形。解题工具当然离不开对三角形的研究。欧几里得把注意力集中在特殊的三角形上:当考虑一个三角形时,着重研究了直角三角形、等腰三角形;当考虑一对三角形时,着重研究了全等三角形和相似三角形。
全等三角形和相似三角形的研究是重要的,因为它与运动、相似这些几何变换密切相关。但作为解题的基本工具,全等三角形与相似三角形的方法就暴露出明显的不足。
一个重要的事实是:随便画一个几何图形,这里面往往没有全等三角形或相似三角形。为了使“全等”、“相似”有用武之地,就要作辅助线。但如何作辅助线,则“法无定法”。几何好学做题难,原因与此有关!
我们着眼于那些任何几何图形中都会出现的三角形对,这就是“共边三角形”和“共角三角形”。
这两种三角形对是名不见经传的。欧几里得以来的几何学家们从来没有给它们以足够的重视。但是,从数学教育界的角度看,它们是顶顶重要的。
两个三角形如果有一条公共边,我们就说这两个三角形是共边三角形。共边三角形在几何图形里到处都是。平面上随便点四个点A、B、C、D,连六条直线,便有许多对共边三角形(如图5-4):△ABC与△ABD,△ADB与△ADC,△ACB与△ACD,△BCA与△BCD,△BDA与△BDC,△CDA与△CDB……
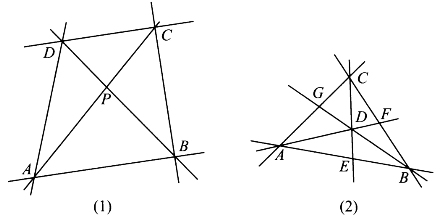
图5-4
在图5-4(1)中,△PAD和△PBC虽不是共边三角形,但它们也有共同点——∠APD=∠BPC。这样有一组对应角相等或互补的一对三角形,叫做共角三角形。在图5-4(1)中出现了许多对共角三角形,如△PAB与△PDC,△PCD与△ACD,△PAB与△PAD等。图5-4(2)中有△AED与△CEB,△DGC与△BGA,△DFB与△GBC……
和共边三角形相联系的基本定理是
共边比例定理(以下简称共边定理) 若直线PQ和直线AB交于M,则![]() 。
。
证明:如图5-5,可知有四种情形。根据我们的基本命题,四种情形都有:

在图5-5情形(1)、(2)中取(1)+(2),情形(3)、(4)中取(1)-(2),可得[1](https://www.chuimin.cn)
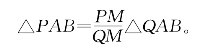
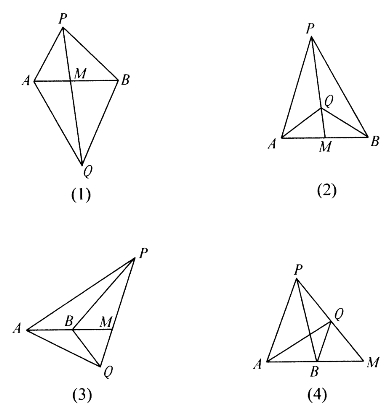
图5-5
尽管这个定理得来不费工夫,但它在图上并不明显。特别是情形(3)、(4),人们往往会忽略这种比例关系。假如在情形(4)中不用共边比例定理,让学生想办法求出△PAB与△QAB面积之比,我想很少有人会想到用尺子沿直线PQ来度量。
和共角三角形相联系的基本定理是
共角比例定理(以下简称共角定理) 在△ABC和△A′B′C′中,∠A=∠A′或∠A+∠A′=180°,则
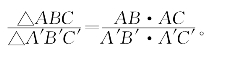
证明:不妨设∠A与∠A′重合或互为邻补角,如图5-6所示。
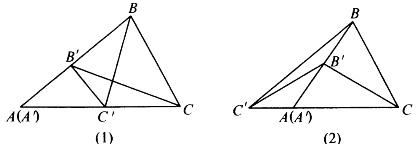
图5-6
这时对(1)、(2)均有
![]()
即得所要等式。
在证明共角定理时,我们用了“运动”,把两个三角形搬到一起,使它们的一对对应角重合或成为邻补角。严格追究起来,这实际上承认了角度、长度和面积是运动下的不变量。如果不引入“运动”的概念,至少也要承认:在△ABC和△A′B′C′中,∠A=∠A′,AB=A′B′,AC=A′C′,则两个三角形面积相等。
不过,在教刚开始学习几何的初中生时,教师可以暂且不去追求逻辑上的绝对严密,而是引导学生用不多的几何知识去解决更多的问题。
相关文章

收敛三角形通常是由多空双方在争斗中出现短暂的休整、调整而形成的。也就是说,在上升趋势中出现收敛三角形,则股价未来向上突破的概率很大;在下跌趋势中出现收敛三角形,则股价未来向下突破的概率更大。......
2025-09-29

相似三角形周长的比等于_________,相似三角形的面积比等于______________________;相似三角形对应角平分线的比、对应中线的比、对应高的比都等于_________.(第1题)(第2题)A.1∶3 B.1∶9 C.1∶12 D.1∶243.如图,在△ABC中,DE∥BC,EF∥A B.若AB=3AD,△ADE的面积为3,则△EFC的面积为( ).A.18 B.12 C.9 D......
2025-09-29

燃烧气体的压力和流速下降,使涡轮所获得能量的等量。图12-32 轴流式涡轮级的叶片形状和速度三角形导流叶片的出口条件就是转子的进口条件。工作叶片(转子)以转速U旋转,相对于工作叶片的空气相对速度W2是,绝对速度V2与工作叶片的转速U之差,此时可以定义相对流动角度β2。以此工作叶片的进口角度β2′设计为等于相对流动角度β2。尤其是,轴向速度的变化会产生等量轴向力,因此工作叶片设计为轴向速度Va一定。......
2025-09-29

一旦股价跌破此位置,则意味着上升三角形形态失效,未来股价存在下跌的风险。第六,上升三角形形态属于典型的整理形态,多数被主力用于在上升过程中清洗浮筹,因而,当该形态出现时,投资者应密切关注股价的运行态势,一旦完成向上突破,则应立即追涨买入。......
2025-09-29

图一图二活动目标1.感知三角形的多种变式,体验图形的翻转与变化。活动准备不同形状三角形共18个;城堡拼图底板2幅(见图四);磁性板3块(见图五)。活动难点运用翻转、旋转变化等方法变换三角形,解决游戏中的问题。活动过程一、游戏“找朋友”1.认识不同变式的三角形提问:看看这些三角形都相同吗?虽然它们长得不一样,但它们都有三条边、三个角,都是三角形。......
2025-09-29
相关推荐